In the geometry of hyperbolic 3-space, the order-3-5 heptagonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
| Order-3-5 heptagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {7,3,5} |
| Coxeter diagram |      |
| Cells | {7,3}  |
| Faces | Heptagon {7} |
| Vertex figure | icosahedron {3,5} |
| Dual | {5,3,7} |
| Coxeter group | [7,3,5] |
| Properties | Regular |
Geometry
The Schläfli symbol of the order-3-5 heptagonal honeycomb is {7,3,5}, with five heptagonal tilings meeting at each edge. The vertex figure of this honeycomb is an icosahedron, {3,5}.
 Poincaré disk model (vertex centered) |
 Ideal surface |
Related polytopes and honeycombs
It is a part of a series of regular polytopes and honeycombs with {p,3,5} Schläfli symbol, and icosahedral vertex figures.
Order-3-5 octagonal honeycomb
| Order-3-5 octagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {8,3,5} |
| Coxeter diagram |  |
| Cells | {8,3}  |
| Faces | Octagon {8} |
| Vertex figure | icosahedron {3,5} |
| Dual | {5,3,8} |
| Coxeter group | [8,3,5] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-3-5 octagonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an octagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order 3-5 heptagonal honeycomb is {8,3,5}, with five octagonal tilings meeting at each edge. The vertex figure of this honeycomb is an icosahedron, {3,5}.
 Poincaré disk model (vertex centered) |
Order-3-5 apeirogonal honeycomb
| Order-3-5 apeirogonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {∞,3,5} |
| Coxeter diagram |  |
| Cells | {∞,3}  |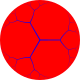
| Faces | Apeirogon {∞} |
| Vertex figure | icosahedron {3,5} |
| Dual | {5,3,∞} |
| Coxeter group | [∞,3,5] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-3-5 apeirogonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-3 apeirogonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-3-5 apeirogonal honeycomb is {∞,3,5}, with five order-3 apeirogonal tilings meeting at each edge. The vertex figure of this honeycomb is an icosahedron, {3,5}.
 Poincaré disk model (vertex centered) |
 Ideal surface |
See also
References
External links
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
