Mixing length model

In fluid dynamics, the mixing length model is a method attempting to describe momentum transfer by turbulence Reynolds stresses within a Newtonian fluid boundary layer by means of an eddy viscosity. The model was developed by Ludwig Prandtl in the early 20th century.^[1] Prandtl himself had reservations about the model,^[2] describing it as, "only a rough approximation,"^[3] but it has been used in numerous fields ever since, including atmospheric science, oceanography and stellar structure.^[4] Also, Ali and Dey^[5] hypothesized an advanced concept of mixing instability.

The mixing length is a distance that a fluid parcel will keep its original characteristics before dispersing them into the surrounding fluid. Here, the bar on the left side of the figure is the mixing length.

Physical intuition

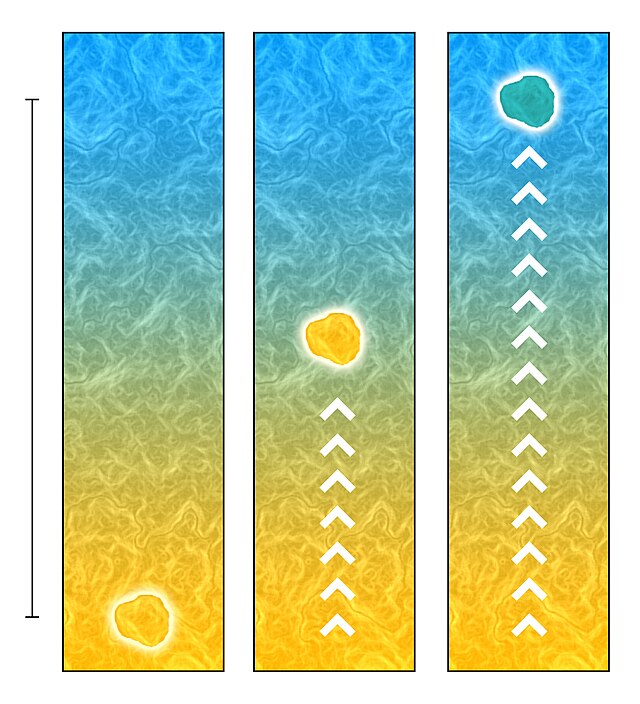
The mixing length is conceptually analogous to the concept of mean free path in thermodynamics: a fluid parcel will conserve its properties for a characteristic length, ${\displaystyle \ \xi '}$, before mixing with the surrounding fluid. Prandtl described that the mixing length,^[6]

may be considered as the diameter of the masses of fluid moving as a whole in each individual case; or again, as the distance traversed by a mass of this type before it becomes blended in with neighbouring masses...

In the figure above, temperature, ${\displaystyle \ T}$, is conserved for a certain distance as a parcel moves across a temperature gradient. The fluctuation in temperature that the parcel experienced throughout the process is ${\displaystyle \ T'}$. So ${\displaystyle \ T'}$ can be seen as the temperature deviation from its surrounding environment after it has moved over this mixing length ${\displaystyle \ \xi '}$.

Mathematical formulation

To begin, we must first be able to express quantities as the sums of their slowly varying components and fluctuating components.

Reynolds decomposition

This process is known as Reynolds decomposition. Temperature can be expressed as:^[7]

$${\displaystyle T={\overline {T}}+T',}$$

where ${\displaystyle {\overline {T}}}$, is the slowly varying component and ${\displaystyle T'}$ is the fluctuating component.

In the above picture, ${\displaystyle T'}$ can be expressed in terms of the mixing length considering a fluid parcel moving in the z-direction:

$${\displaystyle T'=-\xi '{\frac {\partial {\overline {T}}}{\partial z}}.}$$

The fluctuating components of velocity, ${\displaystyle u'}$, ${\displaystyle v'}$, and ${\displaystyle w'}$, can also be expressed in a similar fashion:

$${\displaystyle u'=-\xi '{\frac {\partial {\overline {u}}}{\partial z}},\qquad \ v'=-\xi '{\frac {\partial {\overline {v}}}{\partial z}},\qquad \ w'=-\xi '{\frac {\partial {\overline {w}}}{\partial z}}.}$$

although the theoretical justification for doing so is weaker, as the pressure gradient force can significantly alter the fluctuating components. Moreover, for the case of vertical velocity, ${\displaystyle w'}$ must be in a neutrally stratified fluid.

Taking the product of horizontal and vertical fluctuations gives us:

$${\displaystyle {\overline {u'w'}}={\overline {\xi '^{2}}}\left|{\frac {\partial {\overline {w}}}{\partial z}}\right|{\frac {\partial {\overline {u}}}{\partial z}}.}$$

The eddy viscosity is defined from the equation above as:

$${\displaystyle K_{m}={\overline {\xi '^{2}}}\left|{\frac {\partial {\overline {w}}}{\partial z}}\right|,}$$

so we have the eddy viscosity, ${\displaystyle K_{m}}$ expressed in terms of the mixing length, ${\displaystyle \xi '}$.

See also

• Law of the wall
• Reynolds stress equation model

References

1. Holton, James R. (2004). "Chapter 5 – The Planetary Boundary Layer". Dynamic Meteorology. International Geophysics Series. Vol. 88 (4th ed.). Burlington, MA: Elsevier Academic Press. pp. 124–127.
2. Prandtl, L. (1925). "7. Bericht über Untersuchungen zur ausgebildeten Turbulenz". Z. Angew. Math. Mech. 5 (1): 136–139. Bibcode:1925ZaMM....5..136P. doi:10.1002/zamm.19250050212.
3. Bradshaw, P. (1974). "Possible origin of Prandt's mixing-length theory". Nature. 249 (6): 135–136. Bibcode:1974Natur.249..135B. doi:10.1038/249135b0. S2CID 4218601.
4. Chan, Kwing; Sabatino Sofia (1987). "Validity Tests of the Mixing-Length Theory of Deep Convection". Science. 235 (4787): 465–467. Bibcode:1987Sci...235..465C. doi:10.1126/science.235.4787.465. PMID 17810341. S2CID 21960234.
5. Ali, S.Z.; Dey, S. (2020). "The law of the wall: A new perspective". Physics of Fluids. 36: 121401. doi:10.1063/5.0036387.
6. Prandtl, L. (1926). Proc. Second Intl. Congr. Appl. Mech. Zürich.{{cite book}}: CS1 maint: location missing publisher (link)
7. "Reynolds Decomposition". Florida State University. 6 December 2008. Retrieved 2008-12-06.