Mixed boundary condition

In mathematics, a mixed boundary condition for a partial differential equation defines a boundary value problem in which the solution of the given equation is required to satisfy different boundary conditions on disjoint parts of the boundary of the domain where the condition is stated. Precisely, in a mixed boundary value problem, the solution is required to satisfy a Dirichlet or a Neumann boundary condition in a mutually exclusive way on disjoint parts of the boundary.

Green: Neumann boundary condition; purple: Dirichlet boundary condition.

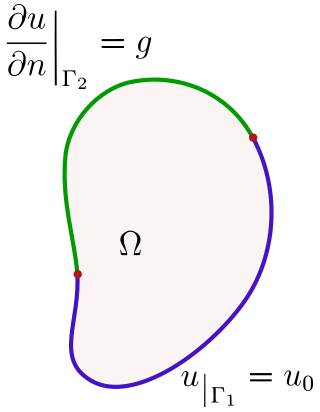
For example, given a solution u to a partial differential equation on a domain Ω with boundary ∂Ω, it is said to satisfy a mixed boundary condition if, consisting ∂Ω of two disjoint parts, Γ
₁ and Γ
₂, such that ∂Ω = Γ
₁ ∪ Γ
₂, u verifies the following equations:

${\displaystyle \left.u\right|_{\Gamma _{1}}=u_{0}}$          and          ${\displaystyle \left.{\frac {\partial u}{\partial n}}\right|_{\Gamma _{2}}=g,}$

where u
₀ and g are given functions defined on those portions of the boundary.^[1]

The mixed boundary condition differs from the Robin boundary condition in that the latter requires a linear combination, possibly with pointwise variable coefficients, of the Dirichlet and the Neumann boundary value conditions to be satisfied on the whole boundary of a given domain.

Historical note

M. Wirtinger, dans une conversation privée, a attiré mon attention sur le probleme suivant: déterminer une fonction u vérifiant l'équation de Laplace dans un certain domaine (D) étant donné, sur une partie (S) de la frontière, les valeurs périphériques de la fonction demandée et, sur le reste (S′) de la frontière du domaine considéré, celles de la dérivée suivant la normale. Je me propose de faire connaitre une solution très générale de cet intéressant problème.^[2]

— Stanisław Zaremba, (Zaremba 1910, §1, p. 313).

The first boundary value problem satisfying a mixed boundary condition was solved by Stanisław Zaremba for the Laplace equation: according to himself, it was Wilhelm Wirtinger who suggested him to study this problem.^[3]

See also

• Dirichlet boundary condition
• Neumann boundary condition
• Cauchy boundary condition
• Robin boundary condition

Notes

1. Obviously, it is not at all necessary to require u
   ₀ and g being functions: they can be distributions or any other kind of generalized functions.
2. (English translation) "Mr. Wirtinger, during a private conversation, has drawn to my attention the following problem: to determine one function u satisfying Laplace's equation on a certain domain (D) being given, on a part (S) of its boundary, the peripheral values of the sought function and, on the remaining part (S′) of the considered domain, the ones of its derivative along the normal. I aim to make known a very general solution of this interesting problem."
3. See (Zaremba 1910, §1, p. 313).

References

• Fichera, Gaetano (1949), "Analisi esistenziale per le soluzioni dei problemi al contorno misti, relativi all'equazione e ai sistemi di equazioni del secondo ordine di tipo ellittico, autoaggiunti", Annali della Scuola Normale Superiore, Serie III (in Italian), 1 (1947) (1–4): 75–100, MR 0035370, Zbl 0035.18603. In the paper "Existential analysis of the solutions of mixed boundary value problems, related to second order elliptic equation and systems of equations, selfadjoint" (English translation of the title), Gaetano Fichera gives the first proofs of existence and uniqueness theorems for the mixed boundary value problem involving a general second order selfadjoint elliptic operators in fairly general domains.
• Guru, Bhag S.; Hızıroğlu, Hüseyin R. (2004), Electromagnetic field theory fundamentals (2nd ed.), Cambridge, UK – New York: Cambridge University Press, p. 593, ISBN 0-521-83016-8.
• Miranda, Carlo (1955), Equazioni alle derivate parziali di tipo ellittico, Ergebnisse der Mathematik und ihrer Grenzgebiete – Neue Folge (in Italian), vol. Heft 2 (1st ed.), Berlin – Göttingen – New York: Springer Verlag, pp. VIII+222, MR 0087853, Zbl 0065.08503.
• Miranda, Carlo (1970) [1955], Partial Differential Equations of Elliptic Type, Ergebnisse der Mathematik und ihrer Grenzgebiete – 2 Folge, vol. Band 2 (2nd Revised ed.), Berlin – Heidelberg – New York: Springer Verlag, pp. XII+370, ISBN 978-3-540-04804-6, MR 0284700, Zbl 0198.14101, translated from the Italian by Zane C. Motteler.
• Zaremba, S. (1910), "Sur un problème mixte relatif à l' équation de Laplace", Bulletin international de l'Académie des Sciences de Cracovie. Classe des Sciences Mathématiques et Naturelles, Serie A: Sciences mathématiques (in French): 313–344, JFM 41.0854.12, translated in Russian as Zaremba, S. (1946), Об одной смешанной задаче, относящейся к уравнению Лапласа, Uspekhi Matematicheskikh Nauk (in Russian), 1 (3-4(13-14)): 125–146, MR 0025032, Zbl 0061.23010.