Lituus (mathematics)

The lituus spiral (/ˈlɪtju.əs/) is a spiral in which the angle θ is inversely proportional to the square of the radius r.

Branch for positive r

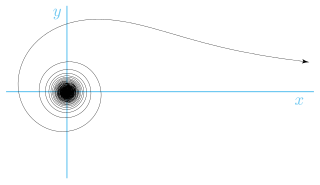
This spiral, which has two branches depending on the sign of r, is asymptotic to the x axis. Its points of inflexion are at

${\displaystyle (\theta ,r)=\left({\tfrac {1}{2}},\pm {\sqrt {2k}}\right).}$

The curve was named for the ancient Roman lituus by Roger Cotes in a collection of papers entitled Harmonia Mensurarum (1722), which was published six years after his death.

Coordinate representations

Polar coordinates

The representations of the lituus spiral in polar coordinates (r, θ) is given by the equation

${\displaystyle r={\frac {a}{\sqrt {\theta }}},}$

where θ ≥ 0 and k ≠ 0.

Cartesian coordinates

The lituus spiral with the polar coordinates r = ⁠a/√θ⁠ can be converted to Cartesian coordinates like any other spiral with the relationships x = r cos θ and y = r sin θ. With this conversion we get the parametric representations of the curve:

${\displaystyle {\begin{aligned}x&={\frac {a}{\sqrt {\theta }}}\cos \theta ,\\y&={\frac {a}{\sqrt {\theta }}}\sin \theta .\\\end{aligned}}}$

These equations can in turn be rearranged to an equation in x and y:

${\displaystyle {\frac {y}{x}}=\tan \left({\frac {a^{2}}{x^{2}+y^{2}}}\right).}$

Derivation of the equation in Cartesian coordinates

1. Divide ${\displaystyle y}$ by ${\displaystyle x}$:${\displaystyle {\frac {y}{x}}={\frac {{\frac {a}{\sqrt {\theta }}}\sin \theta }{{\frac {a}{\sqrt {\theta }}}\cos \theta }}\Rightarrow {\frac {y}{x}}=\tan \theta .}$
2. Solve the equation of the lituus spiral in polar coordinates: ${\displaystyle r={\frac {a}{\sqrt {\theta }}}\Leftrightarrow \theta ={\frac {a^{2}}{r^{2}}}.}$
3. Substitute ${\displaystyle \theta ={\frac {a^{2}}{r^{2}}}}$: ${\displaystyle {\frac {y}{x}}=\tan \left({\frac {a^{2}}{r^{2}}}\right).}$
4. Substitute ${\displaystyle r={\sqrt {x^{2}+y^{2}}}}$: ${\displaystyle {\frac {y}{x}}=\tan \left({\frac {a^{2}}{\left({\sqrt {x^{2}+y^{2}}}\right)^{2}}}\right)\Rightarrow {\frac {y}{x}}=\tan \left({\frac {a^{2}}{x^{2}+y^{2}}}\right).}$

Geometrical properties

Curvature

The curvature of the lituus spiral can be determined using the formula^[1]

${\displaystyle \kappa =\left(8\theta ^{2}-2\right)\left({\frac {\theta }{1+4\theta ^{2}}}\right)^{\frac {2}{3}}.}$

Arc length

In general, the arc length of the lituus spiral cannot be expressed as a closed-form expression, but the arc length of the lituus spiral can be represented as a formula using the Gaussian hypergeometric function:

${\displaystyle L=2{\sqrt {\theta }}\cdot \operatorname {_{2}F_{1}} \left(-{\frac {1}{2}},-{\frac {1}{4}};{\frac {3}{4}};-{\frac {1}{4\theta ^{2}}}\right)-2{\sqrt {\theta _{0}}}\cdot \operatorname {_{2}F_{1}} \left(-{\frac {1}{2}},-{\frac {1}{4}};{\frac {3}{4}};-{\frac {1}{4\theta _{0}^{2}}}\right),}$

where the arc length is measured from θ = θ₀.^[1]

Tangential angle

The tangential angle of the lituus spiral can be determined using the formula^[1]

${\displaystyle \phi =\theta -\arctan 2\theta .}$

References

1. Weisstein, Eric W. "Lituus". MathWorld. Retrieved 2023-02-04.

External links

• "Lituus", Encyclopedia of Mathematics, EMS Press, 2001 [1994].
• Weisstein, Eric W. "Lituus". MathWorld.
• Interactive example using JSXGraph.
• O'Connor, John J.; Robertson, Edmund F., "Lituus", MacTutor History of Mathematics Archive, University of St Andrews.
• https://hsm.stackexchange.com/a/3181 on the history of the lituus curve.