List of Mersenne primes and perfect numbers

Mersenne primes and perfect numbers are two deeply interlinked types of natural numbers in number theory. Mersenne primes, named after the friar Marin Mersenne, are prime numbers that can be expressed as 2^p − 1 for some positive integer p. For example, 3 is a Mersenne prime as it is a prime number and is expressible as 2² − 1.^[1][2] The exponents p corresponding to Mersenne primes must themselves be prime, although the vast majority of primes p do not lead to Mersenne primes—for example, 2¹¹ − 1 = 2047 = 23 × 89.^[3]

Visualization of 6 as a perfect number

Logarithmic graph of the number of digits of the largest known prime number by year, nearly all of which have been Mersenne primes

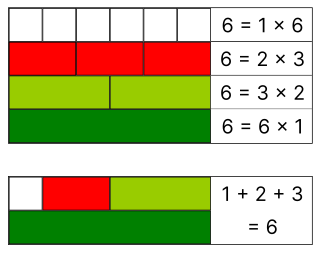
Perfect numbers are natural numbers that equal the sum of their positive proper divisors, which are divisors excluding the number itself. So, 6 is a perfect number because the proper divisors of 6 are 1, 2, and 3, and 1 + 2 + 3 = 6.^[2][4]

Euclid proved c. 300 BCE that every prime expressed as M_p = 2^p − 1 has a corresponding perfect number M_p × (M_p+1)/2 = 2^{p − 1} × (2^p − 1). For example, the Mersenne prime 2² − 1 = 3 leads to the corresponding perfect number 2^{2 − 1} × (2² − 1) = 2 × 3 = 6. In 1747, Leonhard Euler completed what is now called the Euclid–Euler theorem, showing that these are the only even perfect numbers. As a result, there is a one-to-one correspondence between Mersenne primes and even perfect numbers, so a list of one can be converted into a list of the other.^[1][5][6]

It is currently an open problem whether there are infinitely many Mersenne primes and even perfect numbers.^[2][6] The density of Mersenne primes is the subject of the Lenstra–Pomerance–Wagstaff conjecture, which states that the expected number of Mersenne primes less than some given x is (e^γ / log 2) × log log x, where e is Euler's number, γ is Euler's constant, and log is the natural logarithm.^[7][8][9] It is widely believed,^[10] but not proven, that no odd perfect numbers exist; numerous restrictive conditions have been proven,^[10] including a lower bound of 10¹⁵⁰⁰.^[11]

The following is a list of all 52 currently known (as of January 2025^[update]) Mersenne primes and corresponding perfect numbers, along with their exponents p. The largest 18 of these have been discovered by the distributed computing project Great Internet Mersenne Prime Search, or GIMPS; their discoverers are listed as "GIMPS / name", where the name is the person who supplied the computer that made the discovery.^[2] New Mersenne primes are found using the Lucas–Lehmer test (LLT), a primality test for Mersenne primes that is efficient for binary computers.^[2] Due to this efficiency, the largest known prime number has often been a Mersenne prime.^[12]

All possible exponents up to the 48th (p = 57,885,161) have been tested and verified by GIMPS as of October 2021^[update].^[13] Ranks 49 and up are provisional, and may change in the unlikely event that additional primes are discovered between the currently listed ones. Later entries are extremely long, so only the first and last six digits of each number are shown, along with the number of decimal digits.

Table of all 52 currently-known Mersenne primes and corresponding perfect numbers

Rank	p	Mersenne prime		Perfect number		Discovery			Ref.[14]
		Value	Digits	Value	Digits	Date	Discoverer	Method
1	2	3	1	6	1	Ancient times[a]	Known to Ancient Greek mathematicians	Unrecorded	[15][16][17]
2	3	7	1	28	2				[15][16][17]
3	5	31	2	496	3				[15][16][17]
4	7	127	3	8128	4				[15][16][17]
5	13	8191	4	33550336	8	13th century or 1456[b]	Ibn Fallus or anonymous[c]	Trial division	[16][17]
6	17	131071	6	8589869056	10	1588[b]	Pietro Cataldi		[2][20]
7	19	524287	6	137438691328	12				[2][20]
8	31	2147483647	10	230584...952128	19	1772	Leonhard Euler	Trial division with modular restrictions	[21][22]
9	61	230584...693951	19	265845...842176	37	Nov 1883	Ivan Pervushin	Lucas sequences	[23]
10	89	618970...562111	27	191561...169216	54	Jun 1911	Ralph Ernest Powers		[24]
11	107	162259...288127	33	131640...728128	65	Jun 1, 1914			[25]
12	127	170141...105727	39	144740...152128	77	Jan 10, 1876	Édouard Lucas		[26]
13	521	686479...057151	157	235627...646976	314	Jan 30, 1952	Raphael M. Robinson	Lucas–Lehmer test (LLT) on SWAC	[27]
14	607	531137...728127	183	141053...328128	366				[27]
15	1,279	104079...729087	386	541625...291328	770	Jun 25, 1952			[28]
16	2,203	147597...771007	664	108925...782528	1,327	Oct 7, 1952			[29]
17	2,281	446087...836351	687	994970...915776	1,373	Oct 9, 1952			[29]
18	3,217	259117...315071	969	335708...525056	1,937	Sep 8, 1957	Hans Riesel	LLT on BESK	[30]
19	4,253	190797...484991	1,281	182017...377536	2,561	Nov 3, 1961	Alexander Hurwitz	LLT on IBM 7090	[31]
20	4,423	285542...580607	1,332	407672...534528	2,663				[31]
21	9,689	478220...754111	2,917	114347...577216	5,834	May 11, 1963	Donald B. Gillies	LLT on ILLIAC II	[32]
22	9,941	346088...463551	2,993	598885...496576	5,985	May 16, 1963			[32]
23	11,213	281411...392191	3,376	395961...086336	6,751	Jun 2, 1963			[32]
24	19,937	431542...041471	6,002	931144...942656	12,003	Mar 4, 1971	Bryant Tuckerman	LLT on IBM 360/91	[33]
25	21,701	448679...882751	6,533	100656...605376	13,066	Oct 30, 1978	Landon Curt Noll & Laura Nickel	LLT on CDC Cyber 174	[34]
26	23,209	402874...264511	6,987	811537...666816	13,973	Feb 9, 1979	Landon Curt Noll		[34]
27	44,497	854509...228671	13,395	365093...827456	26,790	Apr 8, 1979	Harry L. Nelson & David Slowinski	LLT on Cray-1	[35][36]
28	86,243	536927...438207	25,962	144145...406528	51,924	Sep 25, 1982	David Slowinski		[37]
29	110,503	521928...515007	33,265	136204...862528	66,530	Jan 29, 1988	Walter Colquitt & Luke Welsh	LLT on NEC SX-2	[38][39]
30	132,049	512740...061311	39,751	131451...550016	79,502	Sep 19, 1983	David Slowinski et al. (Cray)	LLT on Cray X-MP	[40]
31	216,091	746093...528447	65,050	278327...880128	130,100	Sep 1, 1985		LLT on Cray X-MP/24	[41][42]
32	756,839	174135...677887	227,832	151616...731328	455,663	Feb 17, 1992		LLT on Harwell Lab's Cray-2	[43]
33	859,433	129498...142591	258,716	838488...167936	517,430	Jan 4, 1994		LLT on Cray C90	[44]
34	1,257,787	412245...366527	378,632	849732...704128	757,263	Sep 3, 1996		LLT on Cray T94	[45][46]
35	1,398,269	814717...315711	420,921	331882...375616	841,842	Nov 13, 1996	GIMPS / Joel Armengaud	LLT / Prime95 on 90 MHz Pentium PC	[47]
36	2,976,221	623340...201151	895,932	194276...462976	1,791,864	Aug 24, 1997	GIMPS / Gordon Spence	LLT / Prime95 on 100 MHz Pentium PC	[48]
37	3,021,377	127411...694271	909,526	811686...457856	1,819,050	Jan 27, 1998	GIMPS / Roland Clarkson	LLT / Prime95 on 200 MHz Pentium PC	[49]
38	6,972,593	437075...193791	2,098,960	955176...572736	4,197,919	Jun 1, 1999	GIMPS / Nayan Hajratwala	LLT / Prime95 on IBM Aptiva with 350 MHz Pentium II processor	[50]
39	13,466,917	924947...259071	4,053,946	427764...021056	8,107,892	Nov 14, 2001	GIMPS / Michael Cameron	LLT / Prime95 on PC with 800 MHz Athlon T-Bird processor	[51]
40	20,996,011	125976...682047	6,320,430	793508...896128	12,640,858	Nov 17, 2003	GIMPS / Michael Shafer	LLT / Prime95 on Dell Dimension PC with 2 GHz Pentium 4 processor	[52]
41	24,036,583	299410...969407	7,235,733	448233...950528	14,471,465	May 15, 2004	GIMPS / Josh Findley	LLT / Prime95 on PC with 2.4 GHz Pentium 4 processor	[53]
42	25,964,951	122164...077247	7,816,230	746209...088128	15,632,458	Feb 18, 2005	GIMPS / Martin Nowak		[54]
43	30,402,457	315416...943871	9,152,052	497437...704256	18,304,103	Dec 15, 2005	GIMPS / Curtis Cooper & Steven Boone	LLT / Prime95 on PC at University of Central Missouri	[55]
44	32,582,657	124575...967871	9,808,358	775946...120256	19,616,714	Sep 4, 2006			[56]
45	37,156,667	202254...220927	11,185,272	204534...480128	22,370,543	Sep 6, 2008	GIMPS / Hans-Michael Elvenich	LLT / Prime95 on PC	[57]
46	42,643,801	169873...314751	12,837,064	144285...253376	25,674,127	Jun 4, 2009[d]	GIMPS / Odd Magnar Strindmo	LLT / Prime95 on PC with 3 GHz Intel Core 2 processor	[58]
47	43,112,609	316470...152511	12,978,189	500767...378816	25,956,377	Aug 23, 2008	GIMPS / Edson Smith	LLT / Prime95 on Dell OptiPlex PC with Intel Core 2 Duo E6600 processor	[57][59][60]
48	57,885,161	581887...285951	17,425,170	169296...130176	34,850,340	Jan 25, 2013	GIMPS / Curtis Cooper	LLT / Prime95 on PC at University of Central Missouri	[61][62]
*	72,633,229	Lowest unverified milestone[e]
49[f]	74,207,281	300376...436351	22,338,618	451129...315776	44,677,235	Jan 7, 2016[g]	GIMPS / Curtis Cooper	LLT / Prime95 on PC with Intel Core i7-4790 processor	[63][64]
50[f]	77,232,917	467333...179071	23,249,425	109200...301056	46,498,850	Dec 26, 2017	GIMPS / Jonathan Pace	LLT / Prime95 on PC with Intel Core i5-6600 processor	[65][66]
51[f]	82,589,933	148894...902591	24,862,048	110847...207936	49,724,095	Dec 7, 2018	GIMPS / Patrick Laroche	LLT / Prime95 on PC with Intel Core i5-4590T processor	[67][68]
*	130,439,863	Lowest untested milestone[e]
52[f]	136,279,841	881694...871551	41,024,320	388692...008576	82,048,640	Oct 12, 2024	GIMPS / Luke Durant	LLT / PRPLL on Nvidia H100 GPU[h]	[69]

Notes

1. The first four perfect numbers were documented by Nicomachus circa 100, and the concept was known (along with corresponding Mersenne primes) to Euclid at the time of his Elements. There is no record of discovery.
2. Islamic mathematicians such as Ismail ibn Ibrahim ibn Fallus (1194–1239) may have known of the fifth through seventh perfect numbers prior to European records.^[18]
3. Found in an anonymous manuscript designated Clm 14908, dated 1456 and 1461. Ibn Fallus' earlier work in the 13th century also mentioned the prime, but was not widely distributed.^[16][19]
4. M_42,643,801 was first reported to GIMPS on April 12, 2009, but was not noticed by a human until June 4, 2009, due to a server error.
5. As of 28 April 2025^[update].^[13] All exponents below the lowest unverified milestone have been checked more than once. All exponents below the lowest untested milestone have been checked at least once.
6. It has not been verified whether any undiscovered Mersenne primes exist between the 48th (M_57,885,161) and the 52nd (M_136,279,841) on this table; the ranking is therefore provisional.
7. M_74,207,281 was first reported to GIMPS on September 17, 2015 but was not noticed by a human until January 7, 2016 due to a server error.
8. First detected as a probable prime using Fermat primality test on an Nvidia A100 GPU on October 11, 2024