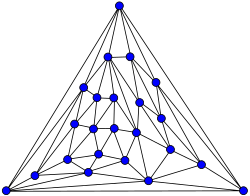
Kittell graph

In the mathematical field of graph theory, the Kittell graph is a planar graph with 23 vertices and 63 edges. Its unique planar embedding has 42 triangular faces.^[1] The Kittell graph is named after Irving Kittell, who used it as a counterexample to Alfred Kempe's flawed proof of the four-color theorem.^[2] Simpler counterexamples include the Errera graph and Poussin graph (both published earlier than Kittell) and the Fritsch graph and Soifer graph.

Kittell graph
The Kittell graph
Vertices	23
Edges	63
Radius	3
Diameter	4
Girth	3
Table of graphs and parameters