Loading AI tools
Measurement of the elevation and depth of features on Earth's surface relative to mean sea level. From Wikipedia, the free encyclopedia
Hypsometry (from Ancient Greek ὕψος (húpsos) 'height' and μέτρον (métron) 'measure')[1][2] is the measurement of the elevation and depth of features of Earth's surface relative to mean sea level.[3]
On Earth, the elevations can take on either positive or negative (below sea level) values. The distribution is theorised to be bimodal due to the difference in density between the lighter continental crust and denser oceanic crust.[4] On other planets within this solar system, elevations are typically unimodal, owing to the lack of plate tectonics on those bodies.[citation needed]
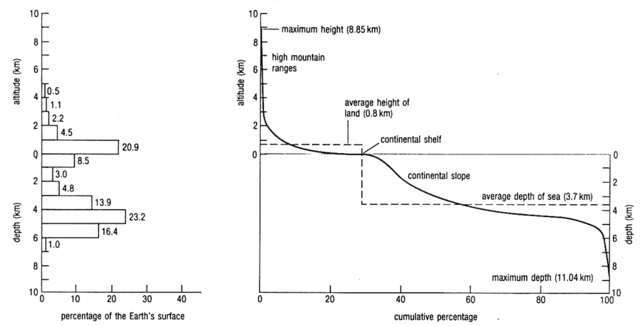
A hypsometric curve is a histogram or cumulative distribution function of elevations in a geographical area. Differences in hypsometric curves between landscapes arise because the geomorphic processes that shape the landscape may be different.
When drawn as a 2-dimensional histogram, a hypsometric curve displays the elevation (y) on the vertical, y-axis and area above the corresponding elevation (x) on the horizontal or x-axis. The curve can also be shown in non-dimensional or standardized form by scaling elevation and area by the maximum values. The non-dimensional hypsometric curve provides a hydrologist or a geomorphologist with a way to assess the similarity of watersheds — and is one of several characteristics used for doing so. The hypsometric integral is a summary measure of the shape of the hypsometric curve.
In the original paper on this topic, Arthur Strahler proposed a curve containing three parameters to fit different hypsometric relations:[5]
where a, d and z are fitting parameters. Subsequent research using two-dimensional landscape evolution models has called the general applicability of this fit into question,[6] as well as the capability of the hypsometric curve to deal with scale-dependent effects. A modified curve with one additional parameter has been proposed to improve the fit.[7]
Hypsometric curves are commonly used in limnology to represent the relationship between lake surface area and depth and calculate total lake volume. These graphs can be used to predict various characteristics of lakes such as productivity, dilution of incoming chemicals, and potential for water mixing.[8]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
![{\displaystyle y=\left[{\frac {d-x}{x}}\cdot {\frac {a}{d-a}}\right]^{z}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fb5cf8d6b8564280d0605694276c309246ab8dc8)
