Dynamic Bayesian network

A dynamic Bayesian network (DBN) is a Bayesian network (BN) which relates variables to each other over adjacent time steps.

Dynamic Bayesian Network composed by 3 variables.

Bayesian Network developed on 3 time steps.

Simplified Dynamic Bayesian Network. All the variables do not need to be duplicated in the graphical model, but they are dynamic, too.

History

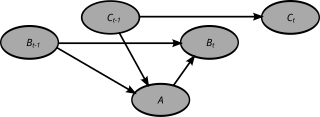
A dynamic Bayesian network (DBN) is often called a "two-timeslice" BN (2TBN) because it says that at any point in time T, the value of a variable can be calculated from the internal regressors and the immediate prior value (time T-1). DBNs were developed by Paul Dagum in the early 1990s at Stanford University's Section on Medical Informatics.^[1][2] Dagum developed DBNs to unify and extend traditional linear state-space models such as Kalman filters, linear and normal forecasting models such as ARMA and simple dependency models such as hidden Markov models into a general probabilistic representation and inference mechanism for arbitrary nonlinear and non-normal time-dependent domains.^[3][4]

Today, DBNs are common in robotics, and have shown potential for a wide range of data mining applications. For example, they have been used in speech recognition, digital forensics, protein sequencing, and bioinformatics. DBN is a generalization of hidden Markov models and Kalman filters.^[5]

DBNs are conceptually related to probabilistic Boolean networks^[6] and can, similarly, be used to model dynamical systems at steady-state.

See also

• Recursive Bayesian estimation
• Probabilistic logic network
• Generalized filtering