Classical Cepheid variable

Classical Cepheids are a type of Cepheid variable star. They are young, population I variable stars that exhibit regular radial pulsations with periods of a few days to a few weeks and visual amplitudes ranging from a few tenths of a magnitude up to about 2 magnitudes. Classical Cepheids are also known as Population I Cepheids, Type I Cepheids, and Delta Cepheid variables.

Hertzsprung–Russell diagram showing the location of several types of variable stars superimposed on a display of the different luminosity classes.

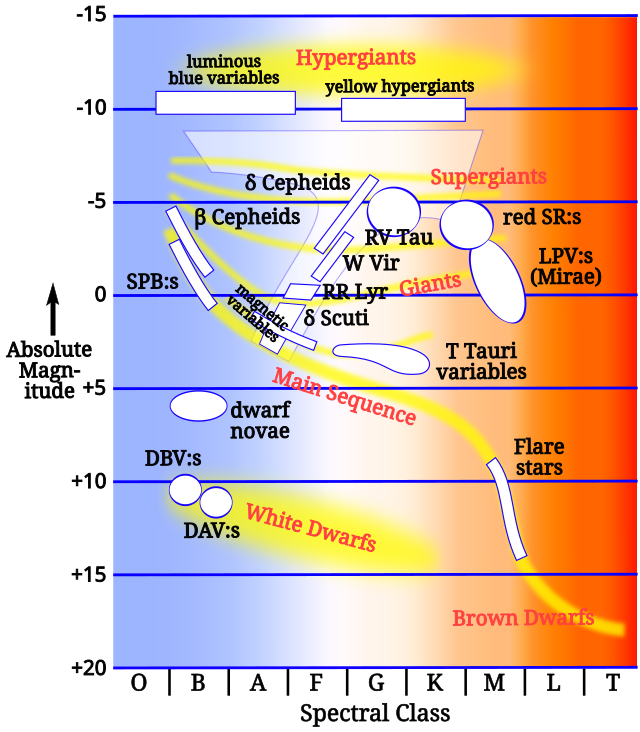
There exists a well-defined relationship between a classical Cepheid variable's luminosity and pulsation period,^[1][2] securing Cepheids as viable standard candles for establishing the galactic and extragalactic distance scales.^[3][4][5][6] Hubble Space Telescope (HST) observations of classical Cepheid variables have enabled firmer constraints on Hubble's law, which describes the expansion rate of the observable Universe.^{[3][4][6][7][8]} Classical Cepheids have also been used to clarify many characteristics of our galaxy, such as the local spiral arm structure and the Sun's distance from the galactic plane.^[5]

Around 800 classical Cepheids are known in the Milky Way galaxy, out of an expected total of over 6,000. Several thousand more are known in the Magellanic Clouds, with more discovered in other galaxies;^[9] the Hubble Space Telescope has identified some in NGC 4603, which is 100 million light years distant.^[10]

Properties

The evolutionary track of 5 M_☉ star crossing the instability strip during a helium burning blue loop

Classical Cepheid variables are 4–20 times more massive than the Sun,^[11] and around 1,000 to 50,000 (over 200,000 for the unusual V810 Centauri) times more luminous.^[12] Spectroscopically they are bright giants or low luminosity supergiants of spectral class F6 – K2. The temperature and spectral type vary as they pulsate. Their radii are a few tens to a few hundred times that of the sun. More luminous Cepheids are cooler and larger and have longer periods. Along with the temperature changes their radii also change during each pulsation (e.g. by ~25% for the longer-period l Car), resulting in brightness variations up to two magnitudes. The brightness changes are more pronounced at shorter wavelengths.^[13]

Cepheid variables may pulsate in a fundamental mode, the first overtone, or rarely a mixed mode. Pulsations in an overtone higher than first are rare but interesting.^[2] The majority of classical Cepheids are thought to be fundamental mode pulsators, although it is not easy to distinguish the mode from the shape of the light curve. Stars pulsating in an overtone are more luminous and larger than a fundamental mode pulsator with the same period.^[14]

When an intermediate mass star (IMS) first evolves away from the main sequence, it crosses the instability strip very rapidly while the hydrogen shell is still burning. When the helium core ignites in an IMS, it may execute a blue loop and crosses the instability strip again, once while evolving to high temperatures and again evolving back towards the asymptotic giant branch. Stars more massive than about 8–12 M_☉ start core helium burning before reaching the red-giant branch and become red supergiants, but may still execute a blue loop through the instability strip. The duration and even existence of blue loops is very sensitive to the mass, metallicity, and helium abundance of the star. In some cases, stars may cross the instability strip for a fourth and fifth time when helium shell burning starts.^{[citation needed]} The rate of change of the period of a Cepheid variable, along with chemical abundances detectable in the spectrum, can be used to deduce which crossing a particular star is making.^[15]

Classical Cepheid variables were B type main-sequence stars earlier than about B7, possibly late O stars, before they ran out of hydrogen in their cores. More massive and hotter stars develop into more luminous Cepheids with longer periods, although it is expected that young stars within our own galaxy, at near solar metallicity, will generally lose sufficient mass by the time they first reach the instability strip that they will have periods of 50 days or less. Above a certain mass, 20–50 M_☉ depending on metallicity, red supergiants will evolve back to blue supergiants rather than execute a blue loop, but they will do so as unstable yellow hypergiants rather than regularly pulsating Cepheid variables. Very massive stars never cool sufficiently to reach the instability strip and do not ever become Cepheids. At low metallicity, for example in the Magellanic Clouds, stars can retain more mass and become more luminous Cepheids with longer periods.^[12]

Light curves

Delta Cephei lightcurve

Phase-folded UBVRI light curves of Delta Cephei, prototype of the classical Cepheids, showing magnitude versus pulsation phase^[16]

A Cepheid light curve is typically asymmetric with a rapid rise to maximum light followed by a slower fall to minimum (e.g. Delta Cephei). This is due to the phase difference between the radius and temperature variations and is considered characteristic of a fundamental mode pulsator, the most common type of type I Cepheid. In some cases the smooth pseudo-sinusoidal light curve shows a "bump", a brief slowing of the decline or even a small rise in brightness, thought to be due to a resonance between the fundamental and second overtone. The bump is most commonly seen on the descending branch for stars with periods around 6 days (e.g. Eta Aquilae). As the period increases, the location of the bump moves closer to the maximum and may cause a double maximum, or become indistinguishable from the primary maximum, for stars having periods around 10 days (e.g. Zeta Geminorum). At longer periods the bump can be seen on the ascending branch of the light curve (e.g. X Cygni),^[17] but for period longer than 20 days the resonance disappears.

A minority of classical Cepheids show nearly symmetric sinusoidal light curves. These are referred to as s-Cepheids, usually have lower amplitudes, and commonly have short periods. The majority of these are thought to be first overtone (e.g. X Sagittarii), or higher, pulsators, although some unusual stars apparently pulsating in the fundamental mode also show this shape of light curve (e.g. S Vulpeculae). Stars pulsating in the first overtone are expected to only occur with short periods in our galaxy, although they may have somewhat longer periods at lower metallicity, for example in the Magellanic Clouds. Higher overtone pulsators and Cepheids pulsating in two overtones at the same time are also more common in the Magellanic Clouds, and they usually have low amplitude somewhat irregular light curves.^[2][18]

Discovery

Historical light curves of W Sagittarii and Eta Aquilae

On September 10, 1784 Edward Pigott detected the variability of Eta Aquilae, the first known representative of the class of classical Cepheid variables. However, the namesake for classical Cepheids is the star Delta Cephei, discovered to be variable by John Goodricke a month later.^[19] Delta Cephei is also of particular importance as a calibrator for the period-luminosity relation since its distance is among the most precisely established for a Cepheid, thanks in part to its membership in a star cluster^[20][21] and the availability of precise Hubble Space Telescope and Hipparcos parallaxes.^[22]

Period-luminosity relation

Main article: Period-luminosity relation

The two Period-Luminosity Characteristics of Classic and Type II Cepheids

A classical Cepheid's luminosity is directly related to its period of variation. The longer the pulsation period, the more luminous the star. The period-luminosity relation for classical Cepheids was discovered in 1908 by Henrietta Swan Leavitt in an investigation of thousands of variable stars in the Magellanic Clouds.^[23] She published it in 1912^[24] with further evidence. Once the period-luminosity relation is calibrated, the luminosity of a given Cepheid whose period is known can be established. Their distance is then found from their apparent brightness. The period-luminosity relation has been calibrated by many astronomers throughout the twentieth century, beginning with Hertzsprung.^[25] Calibrating the period-luminosity relation has been problematic; however, a firm Galactic calibration was established by Benedict et al. 2007 using precise HST parallaxes for 10 nearby classical Cepheids.^[26] Also, in 2008, ESO astronomers estimated with a precision within 1% the distance to the Cepheid RS Puppis, using light echos from a nebula in which it is embedded.^[27] However, that latter finding has been actively debated in the literature.^[28]

The following experimental correlations between a Population I Cepheid's period P and its mean absolute magnitude M_v was established from Hubble Space Telescope trigonometric parallaxes for 10 nearby Cepheids:

${\displaystyle M_{\mathrm {v} }=(-2.43\pm 0.12)\left(\log _{10}P-1\right)-(4.05\pm 0.02)\,}$^[26]

with P measured in days.

The following relations can also be used to calculate the distance d to classical Cepheids:

${\displaystyle 5\log _{10}{d}=V+3.34\log _{10}{P}-2.45(V-I)+10.52\,}$^[26]

or

${\displaystyle 5\log _{10}{d}=V+3.37\log _{10}{P}-2.55(V-I)+10.48\,}$^[29]

I and V represent near infrared and visual apparent mean magnitudes, respectively. The distance d is in parsecs.

Small amplitude Cepheids

Classical Cepheid variables with visual amplitudes below 0.5 magnitudes, almost symmetrical sinusoidal light curves, and short periods, have been defined as a separate group called small amplitude Cepheids. They receive the acronym DCEPS in the GCVS. Periods are generally less than 7 days, although the exact cutoff is still debated.^[30] The term s-Cepheid is used for short period small amplitude Cepheids with sinusoidal light curves that are considered to be first overtone pulsators. They are found near the red edge of the instability strip. Some authors use s-Cepheid as a synonym for the small amplitude DECPS stars, while others prefer to restrict it only to first overtone stars.^[31][32]

Small amplitude Cepheids (DCEPS) include Polaris and FF Aquilae, although both may be pulsating in the fundamental mode. Confirmed first overtone pulsators include BG Crucis and BP Circini.^[33][34]

Uncertainties in Cepheid determined distances

Chief among the uncertainties tied to the Cepheid distance scale are: the nature of the period-luminosity relation in various passbands, the impact of metallicity on both the zero-point and slope of those relations, and the effects of photometric contamination (blending) and a changing (typically unknown) extinction law on classical Cepheid distances. All these topics are actively debated in the literature.^{[4][7][12][35][36][37][38][39][40][41][42][43]}

These unresolved matters have resulted in cited values for the Hubble constant ranging between 60 km/s/Mpc and 80 km/s/Mpc.^{[3][4][6][7][8]} Resolving this discrepancy is one of the foremost problems in astronomy since the cosmological parameters of the Universe may be constrained by supplying a precise value of the Hubble constant.^[6][8]

Examples

Several classical Cepheids have variations that can be recorded with night-by-night, trained naked eye observation, including the prototype Delta Cephei in the far north, Zeta Geminorum and Eta Aquilae ideal for observation around the tropics (near the ecliptic and thus zodiac) and in the far south Beta Doradus. The closest class member is the North Star (Polaris) whose distance is debated and whose present variability is approximately 0.05 of a magnitude.^[6]

Designation (name)	Constellation	Discovery	Maximum Apparent magnitude (mV)[44]	Minimum Apparent magnitude (mV)[44]	Period (days)[44]	Spectral class	Comment
η Aql	Aquila	Edward Pigott, 1784	3m.48	4m.39	07.17664	F6 Ibv
FF Aql	Aquila	Charles Morse Huffer, 1927	5m.18	5m.68	04.47	F5Ia-F8Ia
TT Aql	Aquila		6m.46	7m.7	13.7546	F6-G5
U Aql	Aquila		6m.08	6m.86	07.02393	F5I-II-G1
T Ant	Antlia		5m.00	5m.82	05.898	G5	possibly has unseen companion. Previously thought to be a type II Cepheid[45]
RT Aur	Auriga		5m.00	5m.82	03.73	F8Ibv
l Car	Carina		3m.28	4m.18	35.53584	G5 Iab/Ib
δ Cep	Cepheus	John Goodricke, 1784	3m.48	4m.37	05.36634	F5Ib-G2Ib	double star, visible in binoculars
AX Cir	Circinus		5m.65	6m.09	05.273268	F2-G2II	spectroscopic binary with 5 M☉ B6 companion
BP Cir	Circinus		7m.31	7m.71	02.39810	F2/3II-F6	spectroscopic binary with 4.7 M☉ B6 companion
BG Cru	Crux		5m.34	5m.58	03.3428	F5Ib-G0p
R Cru	Crux		6m.40	7m.23	05.82575	F7Ib/II
S Cru	Crux		6m.22	6m.92	04.68997	F6-G1Ib-II
T Cru	Crux		6m.32	6m.83	06.73331	F6-G2Ib
X Cyg	Cygnus		5m.85	6m.91	16.38633	G8Ib[46]
SU Cyg	Cygnus		6m.44	7m.22	03.84555	F2-G0I-II[47]
β Dor	Dorado		3m.46	4m.08	09.8426	F4-G4Ia-II
ζ Gem	Gemini	Julius Schmidt, 1825	3m.62	4m.18	10.15073	F7Ib to G3Ib
V473 Lyr	Lyra		5m.99	6m.35	01.49078	F6Ib-II
R Mus	Musca		5m.93	6m.73	07.51	F7Ib-G2
S Mus	Musca		5m.89	6m.49	09.66007	F6Ib-G0
S Nor	Norma		6m.12	6m.77	09.75411	F8-G0Ib	brightest member of open cluster NGC 6087
QZ Nor	Norma		8m.71	9m.03	03.786008	F6I	member of open cluster NGC 6067
V340 Nor	Norma		8m.26	8m.60	11.2888	G0Ib	member of open cluster NGC 6067
V378 Nor	Norma		6m.21	6m.23	03.5850	G8Ib
BF Oph	Ophiuchus		6m.93	7m.71	04.06775	F8-K2[48]
RS Pup	Puppis		6m.52	7m.67	41.3876	F8Iab
S Sge	Sagitta	John Ellard Gore, 1885	5m.24	6m.04	08.382086[49]	F6Ib-G5Ib
U Sgr	Sagittarius (in M25)		6m.28	7m.15	06.74523	G1Ib[50]
W Sgr	Sagittarius		4m.29	5m.14	07.59503	F4-G2Ib	Optical double with γ2 Sgr
X Sgr	Sagittarius		4m.20	4m.90	07.01283	F5-G2II
V636 Sco	Scorpius		6m.40	6m.92	06.79671	F7/8Ib/II-G5
R TrA	Triangulum Australe		6m.4	6m.9	03.389	F7Ib/II[50]
S TrA	Triangulum Australe		6m.1	6m.8	06.323	F6II-G2
α UMi (Polaris)	Ursa Minor	Ejnar Hertzsprung, 1911	1m.86	2m.13	03.9696	F8Ib or F8II
AH Vel	Vela		5m.5	5m.89	04.227171	F7Ib-II
S Vul	Vulpecula		8m.69	9m.42	68.464	G0-K2(M1)
T Vul	Vulpecula		5m.41	6m.09	04.435462	F5Ib-G0Ib
U Vul	Vulpecula		6m.73	7m.54	07.990676	F6Iab-G2
SV Vul	Vulpecula		6m.72	7m.79	44.993	F7Iab-K0Iab
SU Cas	Cassiopeia		5m.88	6m.30	01.9	F5II

See also

• RR Lyrae variable
• Stellar pulsation
• Type II Cepheid

References

1. Udalski, A.; Soszynski, I.; Szymanski, M.; Kubiak, M.; Pietrzynski, G.; Wozniak, P.; Zebrun, K. (1999). "The Optical Gravitational Lensing Experiment. Cepheids in the Magellanic Clouds. IV. Catalog of Cepheids from the Large Magellanic Cloud". Acta Astronomica. 49: 223–317. arXiv:astro-ph/9908317. Bibcode:1999AcA....49..223U.
2. Soszynski, I.; Poleski, R.; Udalski, A.; Szymanski, M. K.; Kubiak, M.; Pietrzynski, G.; Wyrzykowski, L.; Szewczyk, O.; Ulaczyk, K. (2008). "The Optical Gravitational Lensing Experiment. The OGLE-III Catalog of Variable Stars. I. Classical Cepheids in the Large Magellanic Cloud". Acta Astronomica. 58: 163. arXiv:0808.2210. Bibcode:2008AcA....58..163S.
3. Freedman, Wendy L.; Madore, Barry F.; Gibson, Brad K.; Ferrarese, Laura; Kelson, Daniel D.; Sakai, Shoko; Mould, Jeremy R.; Kennicutt, Robert C.; Ford, Holland C.; Graham, John A.; Huchra, John P.; Hughes, Shaun M. G.; Illingworth, Garth D.; Macri, Lucas M.; Stetson, Peter B. (2001). "Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant". The Astrophysical Journal. 553 (1): 47–72. arXiv:astro-ph/0012376. Bibcode:2001ApJ...553...47F. doi:10.1086/320638. S2CID 119097691.
4. Tammann, G. A.; Sandage, A.; Reindl, B. (2008). "The expansion field: The value of H 0". The Astronomy and Astrophysics Review. 15 (4): 289. arXiv:0806.3018. Bibcode:2008A&ARv..15..289T. doi:10.1007/s00159-008-0012-y. S2CID 18463474.
5. Majaess, D. J.; Turner, D. G.; Lane, D. J. (2009). "Characteristics of the Galaxy according to Cepheids". Monthly Notices of the Royal Astronomical Society. 398 (1): 263–270. arXiv:0903.4206. Bibcode:2009MNRAS.398..263M. doi:10.1111/j.1365-2966.2009.15096.x. S2CID 14316644.
6. Freedman, Wendy L.; Madore, Barry F. (2010). "The Hubble Constant". Annual Review of Astronomy and Astrophysics. 48: 673–710. arXiv:1004.1856. Bibcode:2010ARA&A..48..673F. doi:10.1146/annurev-astro-082708-101829. S2CID 13909389.
7. Ngeow, C.; Kanbur, S. M. (2006). "The Hubble Constant from Type Ia Supernovae Calibrated with the Linear and Nonlinear Cepheid Period-Luminosity Relations". The Astrophysical Journal. 642 (1): L29–L32. arXiv:astro-ph/0603643. Bibcode:2006ApJ...642L..29N. doi:10.1086/504478. S2CID 17860528.
8. Macri, Lucas M.; Riess, Adam G.; Guzik, Joyce Ann; Bradley, Paul A. (2009). The SH0ES Project: Observations of Cepheids in NGC 4258 and Type Ia SN Hosts. Stellar Pulsation: Challenges for Theory and Observation: Proceedings of the International Conference. AIP Conference Proceedings. Vol. 1170. pp. 23–25. Bibcode:2009AIPC.1170...23M. doi:10.1063/1.3246452.
9. Szabados, L. (2003). "Cepheids: Observational properties, binarity and GAIA". GAIA Spectroscopy: Science and Technology. 298: 237. Bibcode:2003ASPC..298..237S.
10. Newman, J. A.; Zepf, S. E.; Davis, M.; Freedman, W. L.; Madore, B. F.; Stetson, P. B.; Silbermann, N.; Phelps, R. (1999). "A Cepheid Distance to NGC 4603 in Centaurus". The Astrophysical Journal. 523 (2): 506. arXiv:astro-ph/9904368. Bibcode:1999ApJ...523..506N. doi:10.1086/307764. S2CID 15343736.
11. Turner, David G. (1996). "The Progenitors of Classical Cepheid Variables". Journal of the Royal Astronomical Society of Canada. 90: 82. Bibcode:1996JRASC..90...82T.
12. Turner, D. G. (2010). "The PL calibration for Milky Way Cepheids and its implications for the distance scale". Astrophysics and Space Science. 326 (2): 219–231. arXiv:0912.4864. Bibcode:2010Ap&SS.326..219T. doi:10.1007/s10509-009-0258-5. S2CID 119264970.
13. Rodgers, A. W. (1957). "Radius variation and population type of cepheid variables". Monthly Notices of the Royal Astronomical Society. 117: 85–94. Bibcode:1957MNRAS.117...85R. doi:10.1093/mnras/117.1.85.
14. Bono, G.; Gieren, W. P.; Marconi, M.; Fouqué, P. (2001). "On the Pulsation Mode Identification of Short-Period Galactic Cepheids". The Astrophysical Journal. 552 (2): L141. arXiv:astro-ph/0103497. Bibcode:2001ApJ...552L.141B. doi:10.1086/320344. S2CID 16131313.
15. Turner, D. G.; Berdnikov, L. N. (2004). "On the crossing mode of the long-period Cepheid SV Vulpeculae". Astronomy and Astrophysics. 423: 335–340. Bibcode:2004A&A...423..335T. doi:10.1051/0004-6361:20040163.
16. Engle, Scott G.; Guinan, Edward F.; Harper, Graham M.; Neilson, Hilding R.; Remage Evans, Nancy (2014). "The Secret Lives of Cepheids: Evolutionary Changes and Pulsation-induced Shock Heating in the Prototype Classical Cepheid δ Cep". The Astrophysical Journal. 794 (1): 80. arXiv:1409.8628. Bibcode:2014ApJ...794...80E. doi:10.1088/0004-637X/794/1/80. S2CID 119189134.
17. Kovtyukh, V. V.; et al. (January 2005), "Phase-dependent Variation of the Fundamental Parameters of Cepheids. II. Periods Longer than 10 Days", The Astronomical Journal, 129 (1): 433–453, Bibcode:2005AJ....129..433K, doi:10.1086/426339, S2CID 120666782.
18. Soszyñski, I.; Poleski, R.; Udalski, A.; Szymañski, M. K.; Kubiak, M.; Pietrzyñski, G.; Wyrzykowski, Ł.; Szewczyk, O.; Ulaczyk, K. (2010). "The Optical Gravitational Lensing Experiment. The OGLE-III Catalog of Variable Stars. VII. Classical Cepheids in the Small Magellanic Cloud". Acta Astronomica. 60 (1): 17. arXiv:1003.4518. Bibcode:2010AcA....60...17S.
19. Hoskin, M. (1979). "Goodricke, Pigott and the Quest for Variable Stars". Journal for the History of Astronomy. 10: 23–41. Bibcode:1979JHA....10...23H. doi:10.1177/002182867901000103. S2CID 118155505.
20. De Zeeuw, P. T.; Hoogerwerf, R.; De Bruijne, J. H. J.; Brown, A. G. A.; Blaauw, A. (1999). "A HIPPARCOS Census of the Nearby OB Associations". The Astronomical Journal. 117 (1): 354–399. arXiv:astro-ph/9809227. Bibcode:1999AJ....117..354D. doi:10.1086/300682. S2CID 16098861.
21. Majaess, D.; Turner, D.; Gieren, W. (2012). "New Evidence Supporting Cluster Membership for the Keystone Calibrator Delta Cephei". The Astrophysical Journal. 747 (2): 145. arXiv:1201.0993. Bibcode:2012ApJ...747..145M. doi:10.1088/0004-637X/747/2/145. S2CID 118672744.
22. Benedict, G. Fritz; McArthur, B. E.; Fredrick, L. W.; Harrison, T. E.; Slesnick, C. L.; Rhee, J.; Patterson, R. J.; Skrutskie, M. F.; Franz, O. G.; Wasserman, L. H.; Jefferys, W. H.; Nelan, E.; Van Altena, W.; Shelus, P. J.; Hemenway, P. D.; Duncombe, R. L.; Story, D.; Whipple, A. L.; Bradley, A. J. (2002). "Astrometry with the Hubble Space Telescope: A Parallax of the Fundamental Distance Calibrator δ Cephei". The Astronomical Journal. 124 (3): 1695. arXiv:astro-ph/0206214. Bibcode:2002AJ....124.1695B. doi:10.1086/342014. S2CID 42655824.
23. Leavitt, Henrietta S. (1908). "1777 variables in the Magellanic Clouds". Annals of Harvard College Observatory. 60: 87. Bibcode:1907AnHar..60...87L.
24. Leavitt, Henrietta S.; Pickering, Edward C. (1912). "Periods of 25 Variable Stars in the Small Magellanic Cloud". Harvard College Observatory Circular. 173: 1. Bibcode:1912HarCi.173....1L.
25. Hertzsprung, Ejnar (1913). "Über die räumliche Verteilung der Veränderlichen vom δ Cephei-Typus". Astronomische Nachrichten. 196: 201. Bibcode:1913AN....196..201H.
26. Benedict, G. Fritz; McArthur, Barbara E.; Feast, Michael W.; Barnes, Thomas G.; Harrison, Thomas E.; Patterson, Richard J.; Menzies, John W.; Bean, Jacob L.; Freedman, Wendy L. (2007). "Hubble Space Telescope Fine Guidance Sensor Parallaxes of Galactic Cepheid Variable Stars: Period-Luminosity Relations". The Astronomical Journal. 133 (4): 1810. arXiv:astro-ph/0612465. Bibcode:2007AJ....133.1810B. doi:10.1086/511980. S2CID 16384267.
27. Kervella, P.; Mérand, A.; Szabados, L.; Fouqué, P.; Bersier, D.; Pompei, E.; Perrin, G. (2008). "The long-period Galactic Cepheid RS Puppis". Astronomy and Astrophysics. 480 (1): 167–178. arXiv:0802.1501. Bibcode:2008A&A...480..167K. doi:10.1051/0004-6361:20078961. S2CID 14865683.
28. Bond, H. E.; Sparks, W. B. (2009). "On geometric distance determination to the Cepheid RS Puppis from its light echoes". Astronomy and Astrophysics. 495 (2): 371. arXiv:0811.2943. Bibcode:2009A&A...495..371B. doi:10.1051/0004-6361:200810280.
29. Majaess, Daniel; Turner, David; Moni Bidin, Christian; Mauro, Francesco; Geisler, Douglas; Gieren, Wolfgang; Minniti, Dante; Chené, André-Nicolas; Lucas, Philip; Borissova, Jura; Kurtev, Radostn; Dékány, Istvan; Saito, Roberto K. (2011). "New Evidence Supporting Membership for TW Nor in Lyngå 6 and the Centaurus Spiral Arm". The Astrophysical Journal Letters. 741 (2): L27. arXiv:1110.0830. Bibcode:2011ApJ...741L..27M. doi:10.1088/2041-8205/741/2/L27. S2CID 12220317.
30. Samus, N. N.; Durlevich, O. V.; et al. (2009). "VizieR Online Data Catalog: General Catalogue of Variable Stars (Samus+ 2007–2013)". VizieR On-Line Data Catalog: B/GCVS. Originally Published in: 2009yCat....102025S. 1. Bibcode:2009yCat....102025S.
31. Turner, D. G.; Kovtyukh, V. V.; Luck, R. E.; Berdnikov, L. N. (2013). "The Pulsation Mode and Distance of the Cepheid FF Aquilae". The Astrophysical Journal Letters. 772 (1): L10. arXiv:1306.1228. Bibcode:2013ApJ...772L..10T. doi:10.1088/2041-8205/772/1/L10. S2CID 54710833.
32. Antonello, E.; Poretti, E.; Reduzzi, L. (1990). "The separation of S-Cepheids from classical Cepheids and a new definition of the class". Astronomy and Astrophysics. 236: 138. Bibcode:1990A&A...236..138A.
33. Usenko, I. A.; Kniazev, A. Yu.; Berdnikov, L. N.; Kravtsov, V. V. (2014). "Spectroscopic studies of Cepheids in Circinus (AV Cir, BP Cir) and Triangulum Australe (R TrA, S TrA, U TrA, LR TrA)". Astronomy Letters. 40 (12): 800. Bibcode:2014AstL...40..800U. doi:10.1134/S1063773714110061. S2CID 122745580.
34. Evans, N. R.; Szabó, R.; Derekas, A.; Szabados, L.; Cameron, C.; Matthews, J. M.; Sasselov, D.; Kuschnig, R.; Rowe, J. F.; Guenther, D. B.; Moffat, A. F. J.; Rucinski, S. M.; Weiss, W. W. (2015). "Observations of Cepheids with the MOST satellite: Contrast between pulsation modes". Monthly Notices of the Royal Astronomical Society. 446 (4): 4008. arXiv:1411.1730. Bibcode:2015MNRAS.446.4008E. doi:10.1093/mnras/stu2371.
35. Feast, M. W.; Catchpole, R. M. (1997). "The Cepheid period-luminosity zero-point from HIPPARCOS trigonometrical parallaxes". Monthly Notices of the Royal Astronomical Society. 286 (1): L1–L5. Bibcode:1997MNRAS.286L...1F. doi:10.1093/mnras/286.1.l1.
36. Stanek, K. Z.; Udalski, A. (1999). "The Optical Gravitational Lensing Experiment. Investigating the Influence of Blending on the Cepheid Distance Scale with Cepheids in the Large Magellanic Cloud". arXiv:astro-ph/9909346.
37. Udalski, A.; Wyrzykowski, L.; Pietrzynski, G.; Szewczyk, O.; Szymanski, M.; Kubiak, M.; Soszynski, I.; Zebrun, K. (2001). "The Optical Gravitational Lensing Experiment. Cepheids in the Galaxy IC1613: No Dependence of the Period-Luminosity Relation on Metallicity". Acta Astronomica. 51: 221. arXiv:astro-ph/0109446. Bibcode:2001AcA....51..221U.
38. Macri, L. M.; Stanek, K. Z.; Bersier, D.; Greenhill, L. J.; Reid, M. J. (2006). "A New Cepheid Distance to the Maser-Host Galaxy NGC 4258 and Its Implications for the Hubble Constant". The Astrophysical Journal. 652 (2): 1133–1149. arXiv:astro-ph/0608211. Bibcode:2006ApJ...652.1133M. doi:10.1086/508530. S2CID 15728812.
39. Bono, G.; Caputo, F.; Fiorentino, G.; Marconi, M.; Musella, I. (2008). "Cepheids in External Galaxies. I. The Maser-Host Galaxy NGC 4258 and the Metallicity Dependence of Period-Luminosity and Period-Wesenheit Relations". The Astrophysical Journal. 684 (1): 102–117. arXiv:0805.1592. Bibcode:2008ApJ...684..102B. doi:10.1086/589965. S2CID 6275274.
40. Majaess, D.; Turner, D.; Lane, D. (2009). "Type II Cepheids as Extragalactic Distance Candles". Acta Astronomica. 59 (4): 403. arXiv:0909.0181. Bibcode:2009AcA....59..403M.
41. Madore, Barry F.; Freedman, Wendy L. (2009). "Concerning the Slope of the Cepheid Period-Luminosity Relation". The Astrophysical Journal. 696 (2): 1498–1501. arXiv:0902.3747. Bibcode:2009ApJ...696.1498M. doi:10.1088/0004-637X/696/2/1498. S2CID 16325249.
42. Scowcroft, V.; Bersier, D.; Mould, J. R.; Wood, P. R. (2009). "The effect of metallicity on Cepheid magnitudes and the distance to M33". Monthly Notices of the Royal Astronomical Society. 396 (3): 43–47. arXiv:0903.4088. Bibcode:2009MNRAS.396.1287S. doi:10.1111/j.1365-2966.2009.14822.x.
43. Majaess, D. (2010). "The Cepheids of Centaurus A (NGC 5128) and Implications for H0". Acta Astronomica. 60 (2): 121. arXiv:1006.2458. Bibcode:2010AcA....60..121M.
44. Berdnikov, L. N. (2008). "VizieR Online Data Catalog: Photoelectric observations of Cepheids in UBV(RI)c (Berdnikov, 2008)". VizieR On-Line Data Catalog: II/285. Originally Published in: 2008yCat.2285....0B. 2285: 0. Bibcode:2008yCat.2285....0B.
45. Turner, D. G.; Berdnikov, L. N. (2003). "The nature of the Cepheid T Antliae". Astronomy and Astrophysics. 407: 325–334. Bibcode:2003A&A...407..325T. doi:10.1051/0004-6361:20030835.
46. Tomasella, Lina; Munari, Ulisse; Zwitter, Tomaž (2010). "A High-resolution, Multi-epoch Spectral Atlas of Peculiar Stars Including RAVE, GAIA, and HERMES Wavelength Ranges". The Astronomical Journal. 140 (6): 1758. arXiv:1009.5566. Bibcode:2010AJ....140.1758T. doi:10.1088/0004-6256/140/6/1758. S2CID 119188449.
47. Andrievsky, S. M.; Luck, R. E.; Kovtyukh, V. V. (2005). "Phase-dependent Variation of the Fundamental Parameters of Cepheids. III. Periods between 3 and 6 Days". The Astronomical Journal. 130 (4): 1880. Bibcode:2005AJ....130.1880A. doi:10.1086/444541.
48. Kreiken, E. A. (1953). "The Density of Stars of Different Spectral Types. With 1 figure". Zeitschrift für Astrophysik. 32: 125. Bibcode:1953ZA.....32..125K.
49. Watson, Christopher (4 January 2010). "S Sagittae". AAVSO Website. American Association of Variable Star Observers. Retrieved 22 May 2015.
50. Houk, N.; Cowley, A. P. (1975). University of Michigan Catalogue of two-dimensional spectral types for the HD stars. Volume I. Declinations −90° to −53.0°. Bibcode:1975mcts.book.....H.

External links

• The Cepheid Distance Scale: A History, by Nick Allen
• List of classical Cepheids on McMaster Cepheid Photometry and Radial Velocity Data Archive Archived 2021-10-08 at the Wayback Machine
• American Association of Variable Star Observers
• OGLE Atlas of Variable Star Light Curves – Classical Cepheids