Björling problem

In differential geometry, the Björling problem is the problem of finding a minimal surface passing through a given curve with prescribed normal (or tangent planes). The problem was posed and solved by Swedish mathematician Emanuel Gabriel Björling,^[1] with further refinement by Hermann Schwarz.^[2]

Catalan's minimal surface. It can be defined as the minimal surface symmetrically passing through a cycloid.

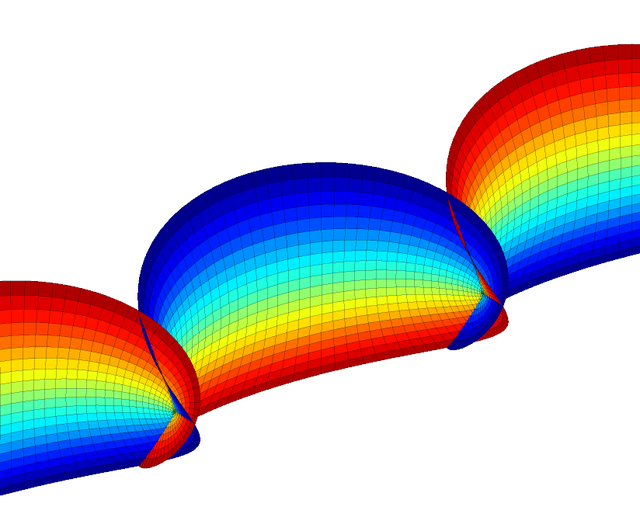
The problem can be solved by extending the surface from the curve using complex analytic continuation. If ${\displaystyle c(s)}$ is a real analytic curve in ${\displaystyle \mathbb {R} ^{3}}$ defined over an interval I, with ${\displaystyle c'(s)\neq 0}$ and a vector field ${\displaystyle n(s)}$ along c such that ${\displaystyle ||n(t)||=1}$ and ${\displaystyle c'(t)\cdot n(t)=0}$, then the following surface is minimal:

${\displaystyle X(u,v)=\Re \left(c(w)-i\int _{w_{0}}^{w}n(w)\times c'(w)\,dw\right)}$

where ${\displaystyle w=u+iv\in \Omega }$, ${\displaystyle u_{0}\in I}$, and ${\displaystyle I\subset \Omega }$ is a simply connected domain where the interval is included and the power series expansions of ${\displaystyle c(s)}$ and ${\displaystyle n(s)}$ are convergent.^[3]

A classic example is Catalan's minimal surface, which passes through a cycloid curve. Applying the method to a semicubical parabola produces the Henneberg surface, and to a circle (with a suitably twisted normal field) a minimal Möbius strip.^[4]

A unique solution always exists. It can be viewed as a Cauchy problem for minimal surfaces, allowing one to find a surface if a geodesic, asymptote or lines of curvature is known. In particular, if the curve is planar and geodesic, then the plane of the curve will be a symmetry plane of the surface.^[5]

References

1. E.G. Björling, Arch. Grunert, IV (1844) pp. 290
2. H.A. Schwarz, J. reine angew. Math. 80 280-300 1875
3. Kai-Wing Fung, Minimal Surfaces as Isotropic Curves in C³: Associated minimal surfaces and the Björling's problem. MIT BA Thesis. 2004 http://ocw.mit.edu/courses/mathematics/18-994-seminar-in-geometry-fall-2004/projects/main1.pdf
4. W.H. Meeks III (1981). "The classification of complete minimal surfaces in R³ with total curvature greater than ${\displaystyle -8\pi }$". Duke Math. J. 48 (3): 523–535. doi:10.1215/S0012-7094-81-04829-8. MR 0630583. Zbl 0472.53010.
5. Björling problem. Encyclopedia of Mathematics. URL: http://www.encyclopediaofmath.org/index.php?title=Bj%C3%B6rling_problem&oldid=23196

External image galleries

• Björling Surfaces, at the Indiana Minimal Surface Archive: http://www.indiana.edu/~minimal/archive/Bjoerling/index.html