Loading AI tools
Quadrilateral with sides of equal length From Wikipedia, the free encyclopedia
In plane Euclidean geometry, a rhombus (pl.: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after the French sweet[1]—also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle.
| Rhombus | |
|---|---|
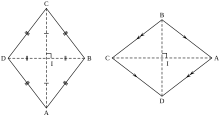 A rhombus in two different orientations | |
| Type | quadrilateral, trapezoid, parallelogram, kite |
| Edges and vertices | 4 |
| Schläfli symbol | { } + { } {2α} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D2), [2], (*22), order 4 |
| Area | (half the product of the diagonals) |
| Properties | convex, isotoxal |
| Dual polygon | rectangle |
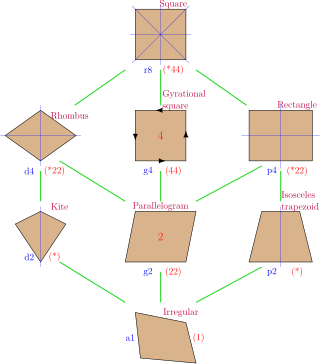
Every rhombus is simple (non-self-intersecting), and is a special case of a parallelogram and a kite. A rhombus with right angles is a square.[2]
The word "rhombus" comes from Ancient Greek: ῥόμβος, romanized: rhómbos, meaning something that spins,[3] which derives from the verb ῥέμβω, romanized: rhémbō, meaning "to turn round and round."[4] The word was used both by Euclid and Archimedes, who used the term "solid rhombus" for a bicone, two right circular cones sharing a common base.[5]
The surface we refer to as rhombus today is a cross section of the bicone on a plane through the apexes of the two cones.

A simple (non-self-intersecting) quadrilateral is a rhombus if and only if it is any one of the following:[6][7]
Every rhombus has two diagonals connecting pairs of opposite vertices, and two pairs of parallel sides. Using congruent triangles, one can prove that the rhombus is symmetric across each of these diagonals. It follows that any rhombus has the following properties:
The first property implies that every rhombus is a parallelogram. A rhombus therefore has all of the properties of a parallelogram: for example, opposite sides are parallel; adjacent angles are supplementary; the two diagonals bisect one another; any line through the midpoint bisects the area; and the sum of the squares of the sides equals the sum of the squares of the diagonals (the parallelogram law). Thus denoting the common side as a and the diagonals as p and q, in every rhombus
Not every parallelogram is a rhombus, though any parallelogram with perpendicular diagonals (the second property) is a rhombus. In general, any quadrilateral with perpendicular diagonals, one of which is a line of symmetry, is a kite. Every rhombus is a kite, and any quadrilateral that is both a kite and parallelogram is a rhombus.
A rhombus is a tangential quadrilateral.[10] That is, it has an inscribed circle that is tangent to all four sides.

The length of the diagonals p = AC and q = BD can be expressed in terms of the rhombus side a and one vertex angle α as
and
These formulas are a direct consequence of the law of cosines.
The inradius (the radius of a circle inscribed in the rhombus), denoted by r, can be expressed in terms of the diagonals p and q as[10]
or in terms of the side length a and any vertex angle α or β as
As for all parallelograms, the area K of a rhombus is the product of its base and its height (h). The base is simply any side length a:
The area can also be expressed as the base squared times the sine of any angle:
or in terms of the height and a vertex angle:
or as half the product of the diagonals p, q:
or as the semiperimeter times the radius of the circle inscribed in the rhombus (inradius):
Another way, in common with parallelograms, is to consider two adjacent sides as vectors, forming a bivector, so the area is the magnitude of the bivector (the magnitude of the vector product of the two vectors), which is the determinant of the two vectors' Cartesian coordinates: K = x1y2 – x2y1.[11]
The dual polygon of a rhombus is a rectangle:[12]
The sides of a rhombus centered at the origin, with diagonals each falling on an axis, consist of all points (x, y) satisfying
The vertices are at and This is a special case of the superellipse, with exponent 1.
| As topological square tilings | As 30-60 degree rhombille tiling | |
|---|---|---|
 |
 |
 |
Convex polyhedra with rhombi include the infinite set of rhombic zonohedrons, which can be seen as projective envelopes of hypercubes.
| Isohedral | Isohedral golden rhombi | 2-isohedral | 3-isohedral | ||
|---|---|---|---|---|---|
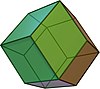 |
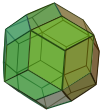 |
 |
 |
 | |
| Trigonal trapezohedron | Rhombic dodecahedron | Rhombic triacontahedron | Rhombic icosahedron | Rhombic enneacontahedron | Rhombohedron |
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.