Set cover problem

The set cover problem is a classical question in combinatorics, computer science, operations research, and complexity theory.

Example of an instance of set cover problem.

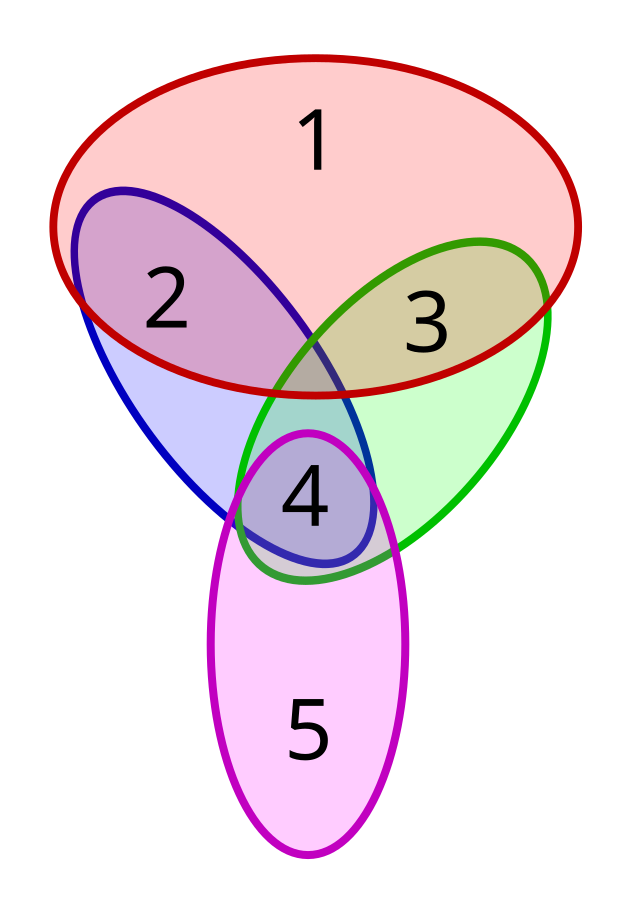
Given a set of elements {1, 2, …, n} (henceforth referred to as the universe, specifying all possible elements under consideration) and a collection, referred to as S, of a given m subsets whose union equals the universe, the set cover problem is to identify a smallest sub-collection of S whose union equals the universe.

For example, consider the universe, U = {1, 2, 3, 4, 5} and the collection of sets S = { {1, 2, 3}, {2, 4}, {3, 4}, {4, 5} }. In this example, m is equal to 4, as there are four subsets that comprise this collection. The union of S is equal to U. However, we can cover all elements with only two sets: { {1, 2, 3}, {4, 5} }‍, see picture, but not with only one set. Therefore, the solution to the set cover problem for this U and S has size 2.

More formally, given a universe ${\displaystyle {\mathcal {U}}}$ and a family ${\displaystyle {\mathcal {S}}}$ of subsets of ${\displaystyle {\mathcal {U}}}$, a set cover is a subfamily ${\displaystyle {\mathcal {C}}\subseteq {\mathcal {S}}}$ of sets whose union is ${\displaystyle {\mathcal {U}}}$.

• In the set cover decision problem, the input is a pair ${\displaystyle ({\mathcal {U}},{\mathcal {S}})}$ and an integer ${\displaystyle k}$; the question is whether there is a set cover of size ${\displaystyle k}$ or less.
• In the set cover optimization problem, the input is a pair ${\displaystyle ({\mathcal {U}},{\mathcal {S}})}$, and the task is to find a set cover that uses the fewest sets.

The decision version of set covering is NP-complete. It is one of Karp's 21 NP-complete problems shown to be NP-complete in 1972. The optimization/search version of set cover is NP-hard.^[1] It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms.^[2]

Variants

In the weighted set cover problem, each set is assigned a positive weight (representing its cost), and the goal is to find a set cover with a smallest weight. The usual (unweighted) set cover corresponds to all sets having a weight of 1.

In the fractional set cover problem, it is allowed to select fractions of sets, rather than entire sets. A fractional set cover is an assignment of a fraction (a number in [0,1]) to each set in ${\displaystyle {\mathcal {S}}}$, such that for each element x in the universe, the sum of fractions of sets that contain x is at least 1. The goal is to find a fractional set cover in which the sum of fractions is as small as possible. Note that a (usual) set cover is equivalent to a fractional set cover in which all fractions are either 0 or 1; therefore, the size of the smallest fractional cover is at most the size of the smallest cover, but may be smaller. For example, consider the universe U = {1, 2, 3} and the collection of sets S = { {1, 2}, {2, 3}, {3, 1} }. The smallest set cover has a size of 2, e.g. { {1, 2}, {2, 3} }. But there is a fractional set cover of size 1.5, in which a 0.5 fraction of each set is taken.

Linear program formulation

The set cover problem can be formulated as the following integer linear program (ILP).^[3]

minimize	${\displaystyle \sum _{s\in {\mathcal {S}}}x_{s}}$		(minimize the number of sets)
subject to	${\displaystyle \sum _{s\colon e\in s}x_{s}\geqslant 1}$	for all ${\displaystyle e\in {\mathcal {U}}}$	(cover every element of the universe)
	${\displaystyle x_{s}\in \{0,1\}}$	for all ${\displaystyle s\in {\mathcal {S}}}$.	(every set is either in the set cover or not)

For a more compact representation of the covering constraint, one can define an incidence matrix ${\displaystyle A}$, where each row corresponds to an element and each column corresponds to a set, and ${\displaystyle A_{e,s}=1}$ if element e is in set s, and ${\displaystyle A_{e,s}=0}$ otherwise. Then, the covering constraint can be written as ${\displaystyle Ax\geqslant 1}$.

Weighted set cover is described by a program identical to the one given above, except that the objective function to minimize is ${\displaystyle \sum _{s\in {\mathcal {S}}}w_{s}x_{s}}$, where ${\displaystyle w_{s}}$ is the weight of set ${\displaystyle s\in {\mathcal {S}}}$.

Fractional set cover is described by a program identical to the one given above, except that ${\displaystyle x_{s}}$ can be non-integer, so the last constraint is replaced by ${\displaystyle 0\leq x_{s}\leq 1}$.

This linear program belongs to the more general class of LPs for covering problems, as all the coefficients in the objective function and both sides of the constraints are non-negative. The integrality gap of the ILP is at most ${\displaystyle \scriptstyle \log n}$ (where ${\displaystyle \scriptstyle n}$ is the size of the universe). It has been shown that its relaxation indeed gives a factor-${\displaystyle \scriptstyle \log n}$ approximation algorithm for the minimum set cover problem.^[4] See randomized rounding#setcover for a detailed explanation.

Hitting set formulation

Set covering is equivalent to the hitting set problem. That is seen by observing that an instance of set covering can be viewed as an arbitrary bipartite graph, with the universe represented by vertices on the left, the sets represented by vertices on the right, and edges representing the membership of elements to sets. The task is then to find a minimum cardinality subset of left-vertices that has a non-trivial intersection with each of the right-vertices, which is precisely the hitting set problem.

In the field of computational geometry, a hitting set for a collection of geometrical objects is also called a stabbing set or piercing set.^[5]

Greedy algorithm

There is a greedy algorithm for polynomial time approximation of set covering that chooses sets according to one rule: at each stage, choose the set that contains the largest number of uncovered elements. This method can be implemented in time linear in the sum of sizes of the input sets, using a bucket queue to prioritize the sets.^[6] It achieves an approximation ratio of ${\displaystyle H(s)}$, where ${\displaystyle s}$ is the size of the set to be covered.^[7] In other words, it finds a covering that may be ${\displaystyle H(n)}$ times as large as the minimum one, where ${\displaystyle H(n)}$ is the ${\displaystyle n}$-th harmonic number: $${\displaystyle H(n)=\sum _{k=1}^{n}{\frac {1}{k}}\leq \ln {n}+1}$$

This greedy algorithm actually achieves an approximation ratio of ${\displaystyle H(s^{\prime })}$ where ${\displaystyle s^{\prime }}$ is the maximum cardinality set of ${\displaystyle S}$. For ${\displaystyle \delta -}$dense instances, however, there exists a ${\displaystyle c\ln {m}}$-approximation algorithm for every ${\displaystyle c>0}$.^[8]

Tight example for the greedy algorithm with k=3

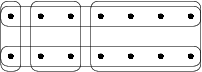
There is a standard example on which the greedy algorithm achieves an approximation ratio of ${\displaystyle \log _{2}(n)/2}$. The universe consists of ${\displaystyle n=2^{(k+1)}-2}$ elements. The set system consists of ${\displaystyle k}$ pairwise disjoint sets ${\displaystyle S_{1},\ldots ,S_{k}}$ with sizes ${\displaystyle 2,4,8,\ldots ,2^{k}}$ respectively, as well as two additional disjoint sets ${\displaystyle T_{0},T_{1}}$, each of which contains half of the elements from each ${\displaystyle S_{i}}$. On this input, the greedy algorithm takes the sets ${\displaystyle S_{k},\ldots ,S_{1}}$, in that order, while the optimal solution consists only of ${\displaystyle T_{0}}$ and ${\displaystyle T_{1}}$. An example of such an input for ${\displaystyle k=3}$ is pictured on the right.

Inapproximability results show that the greedy algorithm is essentially the best-possible polynomial time approximation algorithm for set cover up to lower order terms (see Inapproximability results below), under plausible complexity assumptions. A tighter analysis for the greedy algorithm shows that the approximation ratio is exactly ${\displaystyle \ln {n}-\ln {\ln {n}}+\Theta (1)}$.^[9]

Low-frequency systems

If each element occurs in at most f sets, then a solution can be found in polynomial time that approximates the optimum to within a factor of f using LP relaxation.

If the constraint ${\displaystyle x_{S}\in \{0,1\}}$ is replaced by ${\displaystyle x_{S}\geq 0}$ for all S in ${\displaystyle {\mathcal {S}}}$ in the integer linear program shown above, then it becomes a (non-integer) linear program L. The algorithm can be described as follows:

1. Find an optimal solution O for the program L using some polynomial-time method of solving linear programs.
2. Pick all sets S for which the corresponding variable x_S has value at least 1/f in the solution O.^[10]

Inapproximability results

When ${\displaystyle n}$ refers to the size of the universe, Lund & Yannakakis (1994) showed that set covering cannot be approximated in polynomial time to within a factor of ${\displaystyle {\tfrac {1}{2}}\log _{2}{n}\approx 0.72\ln {n}}$, unless NP has quasi-polynomial time algorithms. Feige (1998) improved this lower bound to ${\displaystyle {\bigl (}1-o(1){\bigr )}\cdot \ln {n}}$ under the same assumptions, which essentially matches the approximation ratio achieved by the greedy algorithm. Raz & Safra (1997) established a lower bound of ${\displaystyle c\cdot \ln {n}}$, where ${\displaystyle c}$ is a certain constant, under the weaker assumption that P${\displaystyle \not =}$NP. A similar result with a higher value of ${\displaystyle c}$ was recently proved by Alon, Moshkovitz & Safra (2006). Dinur & Steurer (2013) showed optimal inapproximability by proving that it cannot be approximated to ${\displaystyle {\bigl (}1-o(1){\bigr )}\cdot \ln {n}}$ unless P${\displaystyle =}$NP.

In low-frequency systems, Dinur et al. (2003) proved it is NP-hard to approximate set cover to better than ${\displaystyle f-1-\epsilon }$. If the Unique games conjecture is true, this can be improved to ${\displaystyle f-\epsilon }$ as proven by Khot & Regev (2008).

Trevisan (2001) proves that set cover instances with sets of size at most ${\displaystyle \Delta }$ cannot be approximated to a factor better than ${\displaystyle \ln \Delta -O(\ln \ln \Delta )}$ unless P${\displaystyle =}$NP, thus making the approximation of ${\displaystyle \ln \Delta +1}$ of the greedy algorithm essentially tight in this case.

Weighted set cover

Relaxing the integer linear program for weighted set cover stated above, one may use randomized rounding to get an ${\displaystyle O(\log n)}$-factor approximation. Non weighted set cover can be adapted to the weighted case.^[11]

Fractional set cover

Related problems

• Hitting set is an equivalent reformulation of Set Cover.
• Vertex cover is a special case of Hitting Set.
• Edge cover is a special case of Set Cover.
• Geometric set cover is a special case of Set Cover when the universe is a set of points in ${\displaystyle \mathbb {R} ^{d}}$ and the sets are induced by the intersection of the universe and geometric shapes (e.g., disks, rectangles).
• Set packing
• Maximum coverage problem is to choose at most k sets to cover as many elements as possible.
• Dominating set is the problem of selecting a set of vertices (the dominating set) in a graph such that all other vertices are adjacent to at least one vertex in the dominating set. The Dominating set problem was shown to be NP complete through a reduction from Set cover.
• Exact cover problem is to choose a set cover with no element included in more than one covering set.
• Red-blue set cover.^[12]
• Set-cover abduction.
• Monotone dualization is a computational problem equivalent to either listing all minimal hitting sets or listing all minimal set covers of a given set family.^[13]

Notes

1. Korte & Vygen 2012, p. 414.
2. Vazirani (2001, p. 15)
3. Vazirani (2001, p. 108)
4. Vazirani (2001, pp. 110–112)
5. Nielsen, Frank (2000-09-06). "Fast stabbing of boxes in high dimensions" (PDF). Theoretical Computer Science. 246 (1): 53–72. doi:10.1016/S0304-3975(98)00336-3. ISSN 0304-3975.
6. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990], "Exercise 35.3-3", Introduction to Algorithms (3rd ed.), MIT Press and McGraw-Hill, p. 1122, ISBN 0-262-03384-4
7. Chvatal, V. (August 1979), "A Greedy Heuristic for the Set-Covering Problem", Mathematics of Operations Research, 4 (3): 233–235, doi:10.1287/moor.4.3.233, JSTOR 3689577
8. Karpinski & Zelikovsky 1998
9. Slavík Petr A tight analysis of the greedy algorithm for set cover. STOC'96, Pages 435-441, doi:10.1145/237814.237991
10. Vazirani (2001, pp. 118–119)
11. Vazirani (2001, Chapter 14)
12. Information., Sandia National Laboratories. United States. Department of Energy. United States. Department of Energy. Office of Scientific and Technical (1999). On the Red-Blue Set Cover Problem. United States. Dept. of Energy. OCLC 68396743.
13. Gainer-Dewar, Andrew; Vera-Licona, Paola (2017), "The minimal hitting set generation problem: algorithms and computation", SIAM Journal on Discrete Mathematics, 31 (1): 63–100, arXiv:1601.02939, doi:10.1137/15M1055024, MR 3590650, S2CID 9240467

References

• Alon, Noga; Moshkovitz, Dana; Safra, Shmuel (2006), "Algorithmic construction of sets for k-restrictions", ACM Trans. Algorithms, 2 (2): 153–177, CiteSeerX 10.1.1.138.8682, doi:10.1145/1150334.1150336, ISSN 1549-6325, S2CID 11922650.
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), Introduction to Algorithms, Cambridge, Mass.: MIT Press and McGraw-Hill, pp. 1033–1038, ISBN 978-0-262-03293-3
• Feige, Uriel (1998), "A threshold of ln n for approximating set cover", Journal of the ACM, 45 (4): 634–652, CiteSeerX 10.1.1.70.5014, doi:10.1145/285055.285059, ISSN 0004-5411, S2CID 52827488.
• Karpinski, Marek; Zelikovsky, Alexander (1998), "Approximating dense cases of covering problems", Proceedings of the DIMACS Workshop on Network Design: Connectivity and Facilities Location, vol. 40, American Mathematical Society, pp. 169–178, ISBN 9780821870846
• Lund, Carsten; Yannakakis, Mihalis (1994), "On the hardness of approximating minimization problems", Journal of the ACM, 41 (5): 960–981, doi:10.1145/185675.306789, ISSN 0004-5411, S2CID 9021065.
• Raz, Ran; Safra, Shmuel (1997), "A sub-constant error-probability low-degree test, and a sub-constant error-probability PCP characterization of NP", STOC '97: Proceedings of the twenty-ninth annual ACM symposium on Theory of computing, ACM, pp. 475–484, ISBN 978-0-89791-888-6.
• Dinur, Irit; Steurer, David (2013), "Analytical approach to parallel repetition", STOC '14: Proceedings of the forty-sixth annual ACM symposium on Theory of computing, ACM, pp. 624–633.
• Vazirani, Vijay V. (2001), Approximation Algorithms (PDF), Springer-Verlag, ISBN 978-3-540-65367-7
• Korte, Bernhard; Vygen, Jens (2012), Combinatorial Optimization: Theory and Algorithms (5 ed.), Springer, ISBN 978-3-642-24487-2
• Cardoso, Nuno; Abreu, Rui (2014), "An Efficient Distributed Algorithm for Computing Minimal Hitting Sets" (PDF), Proceedings of the 25th International Workshop on Principles of Diagnosis, Graz, Austria, doi:10.5281/zenodo.10037{{citation}}: CS1 maint: location missing publisher (link)
• Dinur, Irit; Guruswami, Venkatesan; Khot, Subhash; Regev, Oded (2003), A new multilayered PCP and the hardness of hypergraph vertex cover, Association for Computing Machinery, pp. 595–601, doi:10.1145/780542.780629, ISBN 1581136749
• Khot, Subhash; Regev, Oded (2008), Vertex cover might be hard to approximate to within 2−${\displaystyle \epsilon }$, Journal of Computer and System Sciences, pp. 335–349, doi:10.1016/j.jcss.2007.06.019
• Trevisan, Luca (2001), "Non-approximability results for optimization problems on bounded degree instances", Proceedings of the thirty-third annual ACM symposium on Theory of computing, Association for Computing Machinery, pp. 453–461, doi:10.1145/380752.380839, ISBN 1-58113-349-9

External links

• Benchmarks with Hidden Optimum Solutions for Set Covering, Set Packing and Winner Determination
• A compendium of NP optimization problems - Minimum Set Cover