Top Qs
Timeline
Chat
Perspective
Nine-point hyperbola
Hyperbola constructed from a given triangle and point From Wikipedia, the free encyclopedia
Remove ads
In Euclidean geometry with triangle △ABC, the nine-point hyperbola is an instance of the nine-point conic described by American mathematician Maxime Bôcher in 1892. The celebrated nine-point circle is a separate instance of Bôcher's conic:
- Given a triangle △ABC and a point P in its plane, a conic can be drawn through the following nine points:
- the midpoints of the sides of △ABC,
- the midpoints of the lines joining P to the vertices, and
- the points where these last named lines cut the sides of the triangle.
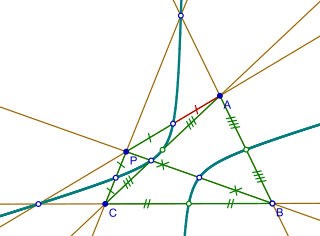
Points of triangle △ABC and given point P
Nine-point hyperbola. The right branch bisects BA, BC, BP; the left bisects PA, PC, AC, and passes through the intersections of lines BC, PA and AB, PC.
The conic is an ellipse if P lies in the interior of △ABC or in one of the regions of the plane separated from the interior by two sides of the triangle; otherwise, the conic is a hyperbola. Bôcher notes that when P is the orthocenter, one obtains the nine-point circle, and when P is on the circumcircle of △ABC, then the conic is an equilateral hyperbola.
Remove ads
Allen
Summarize
Perspective
An approach to the nine-point hyperbola using the analytic geometry of split-complex numbers was devised by E. F. Allen in 1941.[1] Writing , j2 = 1, he uses split-complex arithmetic to express a hyperbola as
It is used as the circumconic of triangle Let Then the nine-point conic is
Allen's description of the nine-point hyperbola followed a development of the nine-point circle that Frank Morley and his son published in 1933. They requisitioned the unit circle in the complex plane as the circumcircle of the given triangle.
In 1953 Allen extended his study to a nine-point conic of a triangle inscribed in any central conic.[2]
Remove ads
Yaglom
For Yaglom, a hyperbola is a Minkowskian circle as in the Minkowski plane. Yaglom's description of this geometry is found in the "Conclusion" chapter of a book that initially addresses Galilean geometry.[3] He considers a triangle inscribed in a "circumcircle" which is in fact a hyperbola. In the Minkowski plane the nine-point hyperbola is also described as a circle:
- … the midpoints of the sides of a triangle △ABC and the feet of its altitudes (as well as the midpoints of the segments joining the orthocenter of △ABC to its vertices) lie on a [Minkowskian] circle S whose radius is half the radius of the circumcircle of the triangle. It is natural to refer to S as the six- (nine-) point circle of the (Minkowskian) triangle △ABC; if △ABC has an incircle s, then the six- (nine-) point circle S of △ABC touches its incircle s (Fig.173).
Remove ads
Others
In 2005 J. A. Scott[4] used the unit hyperbola as the circumconic of triangle ABC and found conditions for it to include six triangle centers: the centroid X(2), the orthocenter X(4), the Fermat points X(13) and X(14), and the Napoleon points X(17) and X(18) as listed in the Encyclopedia of Triangle Centers. Scott’s hyperbola is a Kiepert hyperbola of the triangle.
Christopher Bath[5] describes a nine-point rectangular hyperbola passing through these centers: incenter X(1), the three excenters, the centroid X(2), the de Longchamps point X(20), and the three points obtained by extending the triangle medians to twice their cevian length.
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads





