King effect

In statistics, economics, and econophysics, the king effect is the phenomenon in which the top one or two members of a ranked set show up as clear outliers. These top one or two members are unexpectedly large because they do not conform to the statistical distribution or rank-distribution which the remainder of the set obeys.

Rank-ordering of the population of countries follows a stretched exponential distribution^[1] except in the cases of the two "kings": China and India.

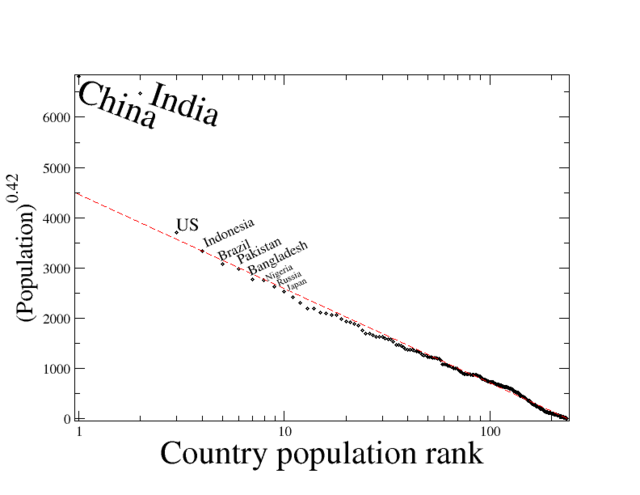
Distributions typically followed include the power-law distribution,^[2] that is a basis for the stretched exponential function,^[1][3] and parabolic fractal distribution. The King effect has been observed in the distribution of:

• French city sizes (where the point representing Paris is the "king", failing to conform to the stretched exponential^[1]), and similarly for other countries with a primate city, such as the United Kingdom (London), and the extreme case of Bangkok (see list of cities in Thailand).
• Country populations (where only the points representing China and India fail to fit a stretched exponential^[1]).

Note, however, that the king effect is not limited to outliers with a positive evaluation attached to their rank: for rankings on an undesirable attribute, there may exist a pauper effect, with a similar detachment of extremely ranked data points from the reasonably distributed portion of the data set.^{[citation needed]}

See also

• Zipf's law
• Didier Sornette