Final topology

In general topology and related areas of mathematics, the final topology^[1] (or coinduced,^[2] weak, colimit, or inductive^[3] topology) on a set ${\displaystyle X,}$ with respect to a family of functions from topological spaces into ${\displaystyle X,}$ is the finest topology on ${\displaystyle X}$ that makes all those functions continuous.

The quotient topology on a quotient space is a final topology, with respect to a single surjective function, namely the quotient map. The disjoint union topology is the final topology with respect to the inclusion maps. The final topology is also the topology that every direct limit in the category of topological spaces is endowed with, and it is in the context of direct limits that the final topology often appears. A topology is coherent with some collection of subspaces if and only if it is the final topology induced by the natural inclusions.

The dual notion is the initial topology, which for a given family of functions from a set ${\displaystyle X}$ into topological spaces is the coarsest topology on ${\displaystyle X}$ that makes those functions continuous.

Definition

Given a set ${\displaystyle X}$ and an ${\displaystyle I}$-indexed family of topological spaces ${\displaystyle \left(Y_{i},\upsilon _{i}\right)}$ with associated functions $${\displaystyle f_{i}:Y_{i}\to X,}$$ the final topology on ${\displaystyle X}$ induced by the family of functions ${\displaystyle {\mathcal {F}}:=\left\{f_{i}:i\in I\right\}}$ is the finest topology ${\displaystyle \tau _{\mathcal {F}}}$ on ${\displaystyle X}$ such that $${\displaystyle f_{i}:\left(Y_{i},\upsilon _{i}\right)\to \left(X,\tau _{\mathcal {F}}\right)}$$

is continuous for each ${\displaystyle i\in I}$.

Explicitly, the final topology may be described as follows:

a subset ${\displaystyle U}$ of ${\displaystyle X}$ is open in the final topology ${\displaystyle \left(X,\tau _{\mathcal {F}}\right)}$ (that is, ${\displaystyle U\in \tau _{\mathcal {F}}}$) if and only if ${\displaystyle f_{i}^{-1}(U)}$ is open in ${\displaystyle \left(Y_{i},\upsilon _{i}\right)}$ for each ${\displaystyle i\in I}$.

The closed subsets have an analogous characterization:

a subset ${\displaystyle C}$ of ${\displaystyle X}$ is closed in the final topology ${\displaystyle \left(X,\tau _{\mathcal {F}}\right)}$ if and only if ${\displaystyle f_{i}^{-1}(C)}$ is closed in ${\displaystyle \left(Y_{i},\upsilon _{i}\right)}$ for each ${\displaystyle i\in I}$.

The family ${\displaystyle {\mathcal {F}}}$ of functions that induces the final topology on ${\displaystyle X}$ is usually a set of functions. But the same construction can be performed if ${\displaystyle {\mathcal {F}}}$ is a proper class of functions, and the result is still well-defined in Zermelo–Fraenkel set theory. In that case there is always a subfamily ${\displaystyle {\mathcal {G}}}$ of ${\displaystyle {\mathcal {F}}}$ with ${\displaystyle {\mathcal {G}}}$ a set, such that the final topologies on ${\displaystyle X}$ induced by ${\displaystyle {\mathcal {F}}}$ and by ${\displaystyle {\mathcal {G}}}$ coincide. For more on this, see for example the discussion here.^[4] As an example, a commonly used variant of the notion of compactly generated space is defined as the final topology with respect to a proper class of functions.^[5]

Examples

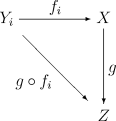
The important special case where the family of maps ${\displaystyle {\mathcal {F}}}$ consists of a single surjective map can be completely characterized using the notion of quotient map. A surjective function ${\displaystyle f:(Y,\upsilon )\to \left(X,\tau \right)}$ between topological spaces is a quotient map if and only if the topology ${\displaystyle \tau }$ on ${\displaystyle X}$ coincides with the final topology ${\displaystyle \tau _{\mathcal {F}}}$ induced by the family ${\displaystyle {\mathcal {F}}=\{f\}}$. In particular: the quotient topology is the final topology on the quotient space induced by the quotient map.

The final topology on a set ${\displaystyle X}$ induced by a family of ${\displaystyle X}$-valued maps can be viewed as a far reaching generalization of the quotient topology, where multiple maps may be used instead of just one and where these maps are not required to be surjections.

Given topological spaces ${\displaystyle X_{i}}$, the disjoint union topology on the disjoint union ${\displaystyle \coprod _{i}X_{i}}$ is the final topology on the disjoint union induced by the natural injections.

Given a family of topologies ${\displaystyle \left(\tau _{i}\right)_{i\in I}}$ on a fixed set ${\displaystyle X,}$ the final topology on ${\displaystyle X}$ with respect to the identity maps ${\displaystyle \operatorname {id} _{\tau _{i}}:\left(X,\tau _{i}\right)\to X}$ as ${\displaystyle i}$ ranges over ${\displaystyle I,}$ call it ${\displaystyle \tau ,}$ is the infimum (or meet) of these topologies ${\displaystyle \left(\tau _{i}\right)_{i\in I}}$ in the lattice of topologies on ${\displaystyle X.}$ That is, the final topology ${\displaystyle \tau }$ is equal to the intersection ${\textstyle \tau =\bigcap _{i\in I}\tau _{i}.}$

Given a topological space ${\displaystyle (X,\tau )}$ and a family ${\displaystyle {\mathcal {C}}=\{C_{i}:i\in I\}}$ of subsets of ${\displaystyle X}$ each having the subspace topology, the final topology ${\displaystyle \tau _{\mathcal {C}}}$ induced by all the inclusion maps of the ${\displaystyle C_{i}}$ into ${\displaystyle X}$ is finer than (or equal to) the original topology ${\displaystyle \tau }$ on ${\displaystyle X.}$ The space ${\displaystyle X}$ is called coherent with the family ${\displaystyle {\mathcal {C}}}$ of subspaces if the final topology ${\displaystyle \tau _{\mathcal {C}}}$ coincides with the original topology ${\displaystyle \tau .}$ In that case, a subset ${\displaystyle U\subseteq X}$ will be open in ${\displaystyle X}$ exactly when the intersection ${\displaystyle U\cap C_{i}}$ is open in ${\displaystyle C_{i}}$ for each ${\displaystyle i\in I.}$ (See the coherent topology article for more details on this notion and more examples.) As a particular case, one of the notions of compactly generated space can be characterized as a certain coherent topology.

The direct limit of any direct system of spaces and continuous maps is the set-theoretic direct limit together with the final topology determined by the canonical morphisms. Explicitly, this means that if ${\displaystyle \operatorname {Sys} _{Y}=\left(Y_{i},f_{ji},I\right)}$ is a direct system in the category Top of topological spaces and if ${\displaystyle \left(X,\left(f_{i}\right)_{i\in I}\right)}$ is a direct limit of ${\displaystyle \operatorname {Sys} _{Y}}$ in the category Set of all sets, then by endowing ${\displaystyle X}$ with the final topology ${\displaystyle \tau _{\mathcal {F}}}$ induced by ${\displaystyle {\mathcal {F}}:=\left\{f_{i}:i\in I\right\},}$ ${\displaystyle \left(\left(X,\tau _{\mathcal {F}}\right),\left(f_{i}\right)_{i\in I}\right)}$ becomes the direct limit of ${\displaystyle \operatorname {Sys} _{Y}}$ in the category Top.

The étalé space of a sheaf is topologized by a final topology.

A first-countable Hausdorff space ${\displaystyle (X,\tau )}$ is locally path-connected if and only if ${\displaystyle \tau }$ is equal to the final topology on ${\displaystyle X}$ induced by the set ${\displaystyle C\left([0,1];X\right)}$ of all continuous maps ${\displaystyle [0,1]\to (X,\tau ),}$ where any such map is called a path in ${\displaystyle (X,\tau ).}$

If a Hausdorff locally convex topological vector space ${\displaystyle (X,\tau )}$ is a Fréchet-Urysohn space then ${\displaystyle \tau }$ is equal to the final topology on ${\displaystyle X}$ induced by the set ${\displaystyle \operatorname {Arc} \left([0,1];X\right)}$ of all arcs in ${\displaystyle (X,\tau ),}$ which by definition are continuous paths ${\displaystyle [0,1]\to (X,\tau )}$ that are also topological embeddings.

Properties

Characterization via continuous maps

Given functions ${\displaystyle f_{i}:Y_{i}\to X,}$ from topological spaces ${\displaystyle Y_{i}}$ to the set ${\displaystyle X}$, the final topology on ${\displaystyle X}$ with respect to these functions ${\displaystyle f_{i}}$ satisfies the following property:

a function ${\displaystyle g}$ from ${\displaystyle X}$ to some space ${\displaystyle Z}$ is continuous if and only if ${\displaystyle g\circ f_{i}}$ is continuous for each ${\displaystyle i\in I.}$

Characteristic property of the final topology

This property characterizes the final topology in the sense that if a topology on ${\displaystyle X}$ satisfies the property above for all spaces ${\displaystyle Z}$ and all functions ${\displaystyle g:X\to Z}$, then the topology on ${\displaystyle X}$ is the final topology with respect to the ${\displaystyle f_{i}.}$

Behavior under composition

Suppose ${\displaystyle {\mathcal {F}}:=\left\{f_{i}:Y_{i}\to X\mid i\in I\right\}}$ is a family of maps, and for every ${\displaystyle i\in I,}$ the topology ${\displaystyle \upsilon _{i}}$ on ${\displaystyle Y_{i}}$ is the final topology induced by some family ${\displaystyle {\mathcal {G}}_{i}}$ of maps valued in ${\displaystyle Y_{i}}$. Then the final topology on ${\displaystyle X}$ induced by ${\displaystyle {\mathcal {F}}}$ is equal to the final topology on ${\displaystyle X}$ induced by the maps ${\displaystyle \left\{f_{i}\circ g~:~i\in I{\text{ and }}g\in {\cal {G_{i}}}\right\}.}$

As a consequence: if ${\displaystyle \tau _{\mathcal {F}}}$ is the final topology on ${\displaystyle X}$ induced by the family ${\displaystyle {\mathcal {F}}:=\left\{f_{i}:i\in I\right\}}$ and if ${\displaystyle \pi :X\to (S,\sigma )}$ is any surjective map valued in some topological space ${\displaystyle (S,\sigma ),}$ then ${\displaystyle \pi$ :\left(X,\tau _{\mathcal {F}}\right)\to (S,\sigma )} is a quotient map if and only if ${\displaystyle (S,\sigma )}$ has the final topology induced by the maps ${\displaystyle \left\{\pi \circ f_{i}~:~i\in I\right\}.}$

By the universal property of the disjoint union topology we know that given any family of continuous maps ${\displaystyle f_{i}:Y_{i}\to X,}$ there is a unique continuous map $${\displaystyle f:\coprod _{i}Y_{i}\to X}$$ that is compatible with the natural injections. If the family of maps ${\displaystyle f_{i}}$ covers ${\displaystyle X}$ (i.e. each ${\displaystyle x\in X}$ lies in the image of some ${\displaystyle f_{i}}$) then the map ${\displaystyle f}$ will be a quotient map if and only if ${\displaystyle X}$ has the final topology induced by the maps ${\displaystyle f_{i}.}$

Effects of changing the family of maps

Throughout, let ${\displaystyle {\mathcal {F}}:=\left\{f_{i}:i\in I\right\}}$ be a family of ${\displaystyle X}$-valued maps with each map being of the form ${\displaystyle f_{i}:\left(Y_{i},\upsilon _{i}\right)\to X}$ and let ${\displaystyle \tau _{\mathcal {F}}}$ denote the final topology on ${\displaystyle X}$ induced by ${\displaystyle {\mathcal {F}}.}$ The definition of the final topology guarantees that for every index ${\displaystyle i,}$ the map ${\displaystyle f_{i}:\left(Y_{i},\upsilon _{i}\right)\to \left(X,\tau _{\mathcal {F}}\right)}$ is continuous.

For any subset ${\displaystyle {\mathcal {S}}\subseteq {\mathcal {F}},}$ the final topology ${\displaystyle \tau _{\mathcal {S}}}$ on ${\displaystyle X}$ will be finer than (and possibly equal to) the topology ${\displaystyle \tau _{\mathcal {F}}}$; that is, ${\displaystyle {\mathcal {S}}\subseteq {\mathcal {F}}}$ implies ${\displaystyle \tau _{\mathcal {F}}\subseteq \tau _{\mathcal {S}},}$ where set equality might hold even if ${\displaystyle {\mathcal {S}}}$ is a proper subset of ${\displaystyle {\mathcal {F}}.}$

If ${\displaystyle \tau }$ is any topology on ${\displaystyle X}$ such that ${\displaystyle \tau \neq \tau _{\mathcal {F}}}$ and ${\displaystyle f_{i}:\left(Y_{i},\upsilon _{i}\right)\to (X,\tau )}$ is continuous for every index ${\displaystyle i\in I,}$ then ${\displaystyle \tau }$ must be strictly coarser than ${\displaystyle \tau _{\mathcal {F}}}$ (meaning that ${\displaystyle \tau \subseteq \tau _{\mathcal {F}}}$ and ${\displaystyle \tau \neq \tau _{\mathcal {F}};}$ this will be written ${\displaystyle \tau \subsetneq \tau _{\mathcal {F}}}$) and moreover, for any subset ${\displaystyle {\mathcal {S}}\subseteq {\mathcal {F}}}$ the topology ${\displaystyle \tau }$ will also be strictly coarser than the final topology ${\displaystyle \tau _{\mathcal {S}}}$ that ${\displaystyle {\mathcal {S}}}$ induces on ${\displaystyle X}$ (because ${\displaystyle \tau _{\mathcal {F}}\subseteq \tau _{\mathcal {S}}}$); that is, ${\displaystyle \tau \subsetneq \tau _{\mathcal {S}}.}$

Suppose that in addition, ${\displaystyle {\mathcal {G}}:=\left\{g_{a}:a\in A\right\}}$ is an ${\displaystyle A}$-indexed family of ${\displaystyle X}$-valued maps ${\displaystyle g_{a}:Z_{a}\to X}$ whose domains are topological spaces ${\displaystyle \left(Z_{a},\zeta _{a}\right).}$ If every ${\displaystyle g_{a}:\left(Z_{a},\zeta _{a}\right)\to \left(X,\tau _{\mathcal {F}}\right)}$ is continuous then adding these maps to the family ${\displaystyle {\mathcal {F}}}$ will not change the final topology on ${\displaystyle X;}$ that is, ${\displaystyle \tau _{{\mathcal {F}}\cup {\mathcal {G}}}=\tau _{\mathcal {F}}.}$ Explicitly, this means that the final topology on ${\displaystyle X}$ induced by the "extended family" ${\displaystyle {\mathcal {F}}\cup {\mathcal {G}}}$ is equal to the final topology ${\displaystyle \tau _{\mathcal {F}}}$ induced by the original family ${\displaystyle {\mathcal {F}}=\left\{f_{i}:i\in I\right\}.}$ However, had there instead existed even just one map ${\displaystyle g_{a_{0}}}$ such that ${\displaystyle g_{a_{0}}:\left(Z_{a_{0}},\zeta _{a_{0}}\right)\to \left(X,\tau _{\mathcal {F}}\right)}$ was not continuous, then the final topology ${\displaystyle \tau _{{\mathcal {F}}\cup {\mathcal {G}}}}$ on ${\displaystyle X}$ induced by the "extended family" ${\displaystyle {\mathcal {F}}\cup {\mathcal {G}}}$ would necessarily be strictly coarser than the final topology ${\displaystyle \tau _{\mathcal {F}}}$ induced by ${\displaystyle {\mathcal {F}};}$ that is, ${\displaystyle \tau _{{\mathcal {F}}\cup {\mathcal {G}}}\subsetneq \tau _{\mathcal {F}}}$ (see this footnote^{[note 1]} for an explanation).

Final topology on the direct limit of finite-dimensional Euclidean spaces

Let $${\displaystyle \mathbb {R} ^{\infty }~:=~\left\{\left(x_{1},x_{2},\ldots \right)\in \mathbb {R} ^{\mathbb {N} }~:~{\text{ all but finitely many }}x_{i}{\text{ are equal to }}0\right\},}$$ denote the space of finite sequences, where ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$ denotes the space of all real sequences. For every natural number ${\displaystyle n\in \mathbb {N} ,}$ let ${\displaystyle \mathbb {R} ^{n}}$ denote the usual Euclidean space endowed with the Euclidean topology and let ${\displaystyle \operatorname {In} _{\mathbb {R} ^{n}}:\mathbb {R} ^{n}\to \mathbb {R} ^{\infty }}$ denote the inclusion map defined by ${\displaystyle \operatorname {In} _{\mathbb {R} ^{n}}\left(x_{1},\ldots ,x_{n}\right):=\left(x_{1},\ldots ,x_{n},0,0,\ldots \right)}$ so that its image is $${\displaystyle \operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right)=\left\{\left(x_{1},\ldots ,x_{n},0,0,\ldots \right)~:~x_{1},\ldots ,x_{n}\in \mathbb {R} \right\}=\mathbb {R} ^{n}\times \left\{(0,0,\ldots )\right\}}$$ and consequently, $${\displaystyle \mathbb {R} ^{\infty }=\bigcup _{n\in \mathbb {N} }\operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right).}$$

Endow the set ${\displaystyle \mathbb {R} ^{\infty }}$ with the final topology ${\displaystyle \tau ^{\infty }}$ induced by the family ${\displaystyle {\mathcal {F}}:=\left\{\;\operatorname {In} _{\mathbb {R} ^{n}}~:~n\in \mathbb {N} \;\right\}}$ of all inclusion maps. With this topology, ${\displaystyle \mathbb {R} ^{\infty }}$ becomes a complete Hausdorff locally convex sequential topological vector space that is not a Fréchet–Urysohn space. The topology ${\displaystyle \tau ^{\infty }}$ is strictly finer than the subspace topology induced on ${\displaystyle \mathbb {R} ^{\infty }}$ by ${\displaystyle \mathbb {R} ^{\mathbb {N} },}$ where ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$ is endowed with its usual product topology. Endow the image ${\displaystyle \operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right)}$ with the final topology induced on it by the bijection ${\displaystyle \operatorname {In} _{\mathbb {R} ^{n}}:\mathbb {R} ^{n}\to \operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right);}$ that is, it is endowed with the Euclidean topology transferred to it from ${\displaystyle \mathbb {R} ^{n}}$ via ${\displaystyle \operatorname {In} _{\mathbb {R} ^{n}}.}$ This topology on ${\displaystyle \operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right)}$ is equal to the subspace topology induced on it by ${\displaystyle \left(\mathbb {R} ^{\infty },\tau ^{\infty }\right).}$ A subset ${\displaystyle S\subseteq \mathbb {R} ^{\infty }}$ is open (respectively, closed) in ${\displaystyle \left(\mathbb {R} ^{\infty },\tau ^{\infty }\right)}$ if and only if for every ${\displaystyle n\in \mathbb {N} ,}$ the set ${\displaystyle S\cap \operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right)}$ is an open (respectively, closed) subset of ${\displaystyle \operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right).}$ The topology ${\displaystyle \tau ^{\infty }}$ is coherent with the family of subspaces ${\displaystyle \mathbb {S}$ :=\left\{\;\operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right)~:~n\in \mathbb {N} \;\right\}.} This makes ${\displaystyle \left(\mathbb {R} ^{\infty },\tau ^{\infty }\right)}$ into an LB-space. Consequently, if ${\displaystyle v\in \mathbb {R} ^{\infty }}$ and ${\displaystyle v_{\bullet }}$ is a sequence in ${\displaystyle \mathbb {R} ^{\infty }}$ then ${\displaystyle v_{\bullet }\to v}$ in ${\displaystyle \left(\mathbb {R} ^{\infty },\tau ^{\infty }\right)}$ if and only if there exists some ${\displaystyle n\in \mathbb {N} }$ such that both ${\displaystyle v}$ and ${\displaystyle v_{\bullet }}$ are contained in ${\displaystyle \operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right)}$ and ${\displaystyle v_{\bullet }\to v}$ in ${\displaystyle \operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right).}$

Often, for every ${\displaystyle n\in \mathbb {N} ,}$ the inclusion map ${\displaystyle \operatorname {In} _{\mathbb {R} ^{n}}}$ is used to identify ${\displaystyle \mathbb {R} ^{n}}$ with its image ${\displaystyle \operatorname {Im} \left(\operatorname {In} _{\mathbb {R} ^{n}}\right)}$ in ${\displaystyle \mathbb {R} ^{\infty };}$ explicitly, the elements ${\displaystyle \left(x_{1},\ldots ,x_{n}\right)\in \mathbb {R} ^{n}}$ and ${\displaystyle \left(x_{1},\ldots ,x_{n},0,0,0,\ldots \right)}$ are identified together. Under this identification, ${\displaystyle \left(\left(\mathbb {R} ^{\infty },\tau ^{\infty }\right),\left(\operatorname {In} _{\mathbb {R} ^{n}}\right)_{n\in \mathbb {N} }\right)}$ becomes a direct limit of the direct system ${\displaystyle \left(\left(\mathbb {R} ^{n}\right)_{n\in \mathbb {N} },\left(\operatorname {In} _{\mathbb {R} ^{m}}^{\mathbb {R} ^{n}}\right)_{m\leq n{\text{ in }}\mathbb {N} },\mathbb {N} \right),}$ where for every ${\displaystyle m\leq n,}$ the map ${\displaystyle \operatorname {In} _{\mathbb {R} ^{m}}^{\mathbb {R} ^{n}}:\mathbb {R} ^{m}\to \mathbb {R} ^{n}}$ is the inclusion map defined by ${\displaystyle \operatorname {In} _{\mathbb {R} ^{m}}^{\mathbb {R} ^{n}}\left(x_{1},\ldots ,x_{m}\right):=\left(x_{1},\ldots ,x_{m},0,\ldots ,0\right),}$ where there are ${\displaystyle n-m}$ trailing zeros.

Categorical description

In the language of category theory, the final topology construction can be described as follows. Let ${\displaystyle Y}$ be a functor from a discrete category ${\displaystyle J}$ to the category of topological spaces Top that selects the spaces ${\displaystyle Y_{i}}$ for ${\displaystyle i\in J.}$ Let ${\displaystyle \Delta }$ be the diagonal functor from Top to the functor category Top^J (this functor sends each space ${\displaystyle X}$ to the constant functor to ${\displaystyle X}$). The comma category ${\displaystyle (Y\,\downarrow \,\Delta )}$ is then the category of co-cones from ${\displaystyle Y,}$ i.e. objects in ${\displaystyle (Y\,\downarrow \,\Delta )}$ are pairs ${\displaystyle (X,f)}$ where ${\displaystyle f=(f_{i}:Y_{i}\to X)_{i\in J}}$ is a family of continuous maps to ${\displaystyle X.}$ If ${\displaystyle U}$ is the forgetful functor from Top to Set and Δ′ is the diagonal functor from Set to Set^J then the comma category ${\displaystyle \left(UY\,\downarrow \,\Delta ^{\prime }\right)}$ is the category of all co-cones from ${\displaystyle UY.}$ The final topology construction can then be described as a functor from ${\displaystyle \left(UY\,\downarrow \,\Delta ^{\prime }\right)}$ to ${\displaystyle (Y\,\downarrow \,\Delta ).}$ This functor is left adjoint to the corresponding forgetful functor.

See also

• Direct limit – Special case of colimit in category theory
• Induced topology – Inherited topologyPages displaying short descriptions of redirect targets
• Initial topology – Coarsest topology making certain functions continuous
• LB-space
• LF-space – Topological vector space

Notes

1. By definition, the map ${\displaystyle g_{a_{0}}:\left(Z_{a_{0}},\zeta _{a_{0}}\right)\to \left(X,\tau _{\mathcal {F}}\right)}$ not being continuous means that there exists at least one open set ${\displaystyle U\in \tau _{\mathcal {F}}}$ such that ${\displaystyle g_{a_{0}}^{-1}(U)}$ is not open in ${\displaystyle \left(Z_{a_{0}},\zeta _{a_{0}}\right).}$ In contrast, by definition of the final topology ${\displaystyle \tau _{{\mathcal {F}}\cup \{g_{a_{0}}\}},}$ the map ${\displaystyle g_{a_{0}}:\left(Z_{a_{0}},\zeta _{a_{0}}\right)\to \left(X,\tau _{{\mathcal {F}}\cup \{g_{a_{0}}\}}\right)}$ must be continuous. So the reason why ${\displaystyle \tau _{{\mathcal {F}}\cup {\mathcal {G}}}}$ must be strictly coarser, rather than strictly finer, than ${\displaystyle \tau _{\mathcal {F}}}$ is because the failure of the map ${\displaystyle g_{a_{0}}:\left(Z_{a_{0}},\zeta _{a_{0}}\right)\to \left(X,\tau _{\mathcal {F}}\right)}$ to be continuous necessitates that one or more open subsets of ${\displaystyle \tau _{\mathcal {F}}}$ must be "removed" in order for ${\displaystyle g_{a_{0}}}$ to become continuous. Thus ${\displaystyle \tau _{{\mathcal {F}}\cup \{g_{a_{0}}\}}}$ is just ${\displaystyle \tau _{\mathcal {F}}}$ but some open sets "removed" from ${\displaystyle \tau _{\mathcal {F}}.}$

Citations

1. Bourbaki, Nicolas (1989). General topology. Berlin: Springer-Verlag. p. 32. ISBN 978-3-540-64241-1.
2. Singh, Tej Bahadur (May 5, 2013). Elements of Topology. CRC Press. ISBN 9781482215663. Retrieved July 21, 2020.
3. Császár, Ákos (1978). General topology. Bristol [England]: A. Hilger. p. 317. ISBN 0-85274-275-4.
4. "Set theoretic issues in the definition of k-space or final topology wrt a proper class of functions". Mathematics Stack Exchange.
5. Brown 2006, Section 5.9, p. 182.

References

• Brown, Ronald (June 2006). Topology and Groupoids. North Charleston: CreateSpace. ISBN 1-4196-2722-8.
• Willard, Stephen (1970). General Topology. Addison-Wesley Series in Mathematics. Reading, MA: Addison-Wesley. ISBN 9780201087079. Zbl 0205.26601.. (Provides a short, general introduction in section 9 and Exercise 9H)
• Willard, Stephen (2004) [1970]. General Topology. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-43479-7. OCLC 115240.