Top Qs
Timeline
Chat
Perspective
Dihedral symmetry in three dimensions
Regular polygonal symmetry From Wikipedia, the free encyclopedia
Remove ads
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dihn (for n ≥ 2).
Remove ads
Types
Summarize
Perspective
There are 3 types of dihedral symmetry in three dimensions, each shown below in 3 notations: Schönflies notation, Coxeter notation, and orbifold notation.
- Chiral
- Dn, [n,2]+, (22n) of order 2n – dihedral symmetry or para-n-gonal group (abstract group: Dihn).
- Achiral
- Dnh, [n,2], (*22n) of order 4n – prismatic symmetry or full ortho-n-gonal group (abstract group: Dihn × Z2).
- Dnd (or Dnv), [2n,2+], (2*n) of order 4n – antiprismatic symmetry or full gyro-n-gonal group (abstract group: Dih2n).
For a given n, all three have n-fold rotational symmetry about one axis (rotation by an angle of 360°/n does not change the object), and 2-fold rotational symmetry about a perpendicular axis, hence about n of those. For n = ∞, they correspond to three Frieze groups. Schönflies notation is used, with Coxeter notation in brackets, and orbifold notation in parentheses. The term horizontal (h) is used with respect to a vertical axis of rotation.
In 2D, the symmetry group Dn includes reflections in lines. When the 2D plane is embedded horizontally in a 3D space, such a reflection can either be viewed as the restriction to that plane of a reflection through a vertical plane, or as the restriction to the plane of a rotation about the reflection line, by 180°. In 3D, the two operations are distinguished: the group Dn contains rotations only, not reflections. The other group is pyramidal symmetry Cnv of the same order, 2n.
With reflection symmetry in a plane perpendicular to the n-fold rotation axis, we have Dnh, [n], (*22n).
Dnd (or Dnv), [2n,2+], (2*n) has vertical mirror planes between the horizontal rotation axes, not through them. As a result, the vertical axis is a 2n-fold rotoreflection axis.
Dnh is the symmetry group for a regular n-sided prism and also for a regular n-sided bipyramid. Dnd is the symmetry group for a regular n-sided antiprism, and also for a regular n-sided trapezohedron. Dn is the symmetry group of a partially rotated prism.
n = 1 is not included because the three symmetries are equal to other ones:
- D1 and C2: group of order 2 with a single 180° rotation.
- D1h and C2v: group of order 4 with a reflection in a plane and a 180° rotation about a line in that plane.
- D1d and C2h: group of order 4 with a reflection in a plane and a 180° rotation about a line perpendicular to that plane.
For n = 2 there is not one main axis and two additional axes, but there are three equivalent ones.
- D2, [2,2]+, (222) of order 4 is one of the three symmetry group types with the Klein four-group as abstract group. It has three perpendicular 2-fold rotation axes. It is the symmetry group of a cuboid with an S written on two opposite faces, in the same orientation.
- D2h, [2,2], (*222) of order 8 is the symmetry group of a cuboid.
- D2d, [4,2+], (2*2) of order 8 is the symmetry group of e.g.:
- A square cuboid with a diagonal drawn on one square face, and a perpendicular diagonal on the other one.
- A regular tetrahedron scaled in the direction of a line connecting the midpoints of two opposite edges (D2d is a subgroup of Td; by scaling, we reduce the symmetry).
Remove ads
Subgroups
 D2h, [2,2], (*222) |
 D4h, [4,2], (*224) |
For Dnh, [n,2], (*22n), order 4n
- Cnh, [n+,2], (n*), order 2n
- Cnv, [n,1], (*nn), order 2n
- Dn, [n,2]+, (22n), order 2n
For Dnd, [2n,2+], (2*n), order 4n
- S2n, [2n+,2+], (n×), order 2n
- Cnv, [n+,2], (n*), order 2n
- Dn, [n,2]+, (22n), order 2n
Dnd is also subgroup of D2nh.
Examples
Dnh, [2,n], (*22n):
 prisms |
D5h, [2,5], (*225):
 Pentagrammic prism |
 Pentagrammic antiprism |
D4d, [8,2+], (2*4):
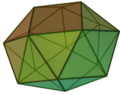 Snub square antiprism |
D5d, [10,2+], (2*5):
 Pentagonal antiprism |
 Pentagrammic crossed-antiprism |
 pentagonal trapezohedron |
D17d, [34,2+], (2*17):
 Heptadecagonal antiprism |
See also
References
- Coxeter, H. S. M. and Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.
{{cite book}}: CS1 maint: multiple names: authors list (link) - N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.5 Spherical Coxeter groups
- Conway, John Horton; Huson, Daniel H. (2002), "The Orbifold Notation for Two-Dimensional Groups", Structural Chemistry, 13 (3), Springer Netherlands: 247–257, doi:10.1023/A:1015851621002, S2CID 33947139
Remove ads
External links
- Graphic overview of the 32 crystallographic point groups – form the first parts (apart from skipping n=5) of the 7 infinite series and 5 of the 7 separate 3D point groups
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads








