Zindlerkurve

Eine Zindlerkurve ist eine geschlossene doppelpunktfreie Kurve in der Ebene mit der Eigenschaft, dass

(L) alle Sehnen, die die Kurve halbieren, gleich lang sind.

Zindler-Kurve: Jede der gleich langen Sehnen halbiert die Länge der Kurve und ihren Flächeninhalt.

Beispiele von Zindlerkurven: konvexe (rot) und nicht konvexe

Das einfachste Beispiel für eine Zindlerkurve ist ein Kreis. Konrad Zindler entdeckte 1921, dass es weitere solche Kurven gibt, und beschrieb ein Konstruktionsverfahren. Herman Auerbach war 1938 der Erste, der den Namen Zindlerkurven (courbes de Zindler) benutzte.

Eine äquivalente charakterisierende Eigenschaft der Zindlerkurven ist, dass

(F) alle Sehnen, die die innere Fläche der geschlossenen Kurve halbieren, gleich lang sind. Es handelt sich dabei um die gleichen Sehnen, die auch die Kurvenlänge halbieren.

Beispiele:^[1]
Jede der von dem Scharparameter ${\displaystyle a}$ abhängigen Kurven (der Einfachheit halber in der komplexen Ebene beschrieben)

${\displaystyle z(u)=x(u)+iy(u)=e^{2iu}+2e^{-iu}+ae^{iu/2}\;,\ u\in [0,4\pi ]\;,}$

ist für ${\displaystyle a>4}$ eine Zindlerkurve.
Für ${\displaystyle a\geq 24}$ ist die Kurve sogar konvex.
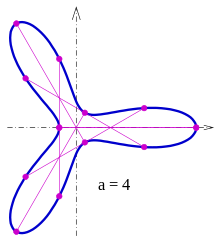
In der Zeichnung sind die Kurven für ${\displaystyle a=8}$ (blau), ${\displaystyle a=16}$ (grün) und ${\displaystyle a=24}$ (rot) zu sehen.
Ab ${\displaystyle a\geq 8}$ ist die Kurve von einem Gleichdick ableitbar.

Die Kurve mit a=4 ist KEINE Zindlerkurve, weil es Sehnen gibt, die einen dritten Punkt mit der Kurve gemeinsam haben.

Nachweis der Eigenschaft (L): Aus der Ableitung

${\displaystyle z'(u)=i{\Big (}2e^{2iu}-2e^{-iu}+{\frac {a}{2}}e^{iu/2}{\Big )}\;}$ ergibt sich

${\displaystyle |z'(u)|^{2}=z'(u){\overline {z'(u)}}=\cdots =8+{\frac {a^{2}}{4}}-8\cos 3u\;.}$

Damit ist ${\displaystyle |z'(u)|}$ eine ${\displaystyle 2\pi }$-periodische Funktion und es gilt für jedes ${\displaystyle u_{0}}$ die Gleichung

${\displaystyle \int _{u_{0}}^{u_{0}+2\pi }|z'(u)|\,du=\int _{0}^{2\pi }|z'(u)|\,du\;.}$

Letzteres ist damit auch die halbe Länge der Kurve. Die Sehnen, die die Kurvenlänge halbieren, lassen sich also durch Kurvenpunkte ${\displaystyle \;z(u_{0})\;,\;z(u_{0}+2\pi )\;}$ mit ${\displaystyle u_{0}\in [0,4\pi ]}$ beschreiben. Für die Länge solch einer Sehne ergibt sich

${\displaystyle |z(u_{0}+2\pi )-z(u_{0})|=\cdots =|2ae^{iu_{0}/2}|=2a}$

und diese ist damit unabhängig von ${\displaystyle u_{0}}$.

Für ${\displaystyle a=4}$ gibt es unter den hier beschriebenen Sehnen welche, die mit der Kurve einen dritten Punkt gemeinsam haben (s. Bild). Also können nur die Kurven der Beispielschar mit ${\displaystyle a>4}$ Zindlerkurven sein. (Der Beweis, dass für ${\displaystyle a>4}$ die verwendeten Sehnen keine weiteren Punkte mit der Kurve gemeinsam haben, wurde hier nicht geführt.)

Literatur

• Herman Auerbach: Sur un problème de M. Ulam concernant l’équilibre des corps flottants. (PDF; 796 kB), Studia Mathematica 7, 1938, S. 121–142.
• K. L. Mampel: Über Zindlerkurven. Journal für reine und angewandte Mathematik 234, 1969, S. 12–44.
• Konrad Zindler: Über konvexe Gebilde. II. Teil. Monatshefte für Mathematik und Physik 31, 1921, S. 25–56.

Einzelnachweise

1. W. Wunderlich: Algebraische Beispiele ebener und räumlicher Zindler-Kurven. Publ. Math. Debrecen 24 (1977), 289–297 (S. 291).