Satz von Poncelet-Steiner

Der Satz von Poncelet und Steiner ist ein Satz aus der synthetischen Geometrie. Er beruht auf einer Vermutung von Jean Victor Poncelet aus 1822 und wurde 1833 von Jakob Steiner bewiesen.^[1]

Satz von Poncelet-Steiner

Der Satz besagt, dass jede Konstruktion, die mit Zirkel und Lineal durchführbar ist, auch nur mit dem Lineal durchführbar ist, sofern ein fester Kreis und dessen Mittelpunkt gegeben sind.

Steiner beweist den Satz, indem er zeigt, wie die Elementaraufgaben der Konstruktion unter Verwendung ausschließlich jener eingeschränkten Hilfsmittel durchgeführt werden können.

Der Satz hat ein Pendant im Satz von Mohr-Mascheroni, der besagt, dass mit Zirkel und Lineal ausführbare Konstruktionen – also die in der klassischen antiken Geometrie nach Euklid betrachteten Konstruktionsaufgaben – auch mit dem Zirkel allein ausführbar sind.

Konstruktionen

Zu einem Kreisdurchmesser eine Parallele durch einen beliebigen Punkt ziehen

Konstruktion nach Steiner: zu einem Kreisdurchmesser eine Parallele durch einen beliebigen Punkt ziehen.

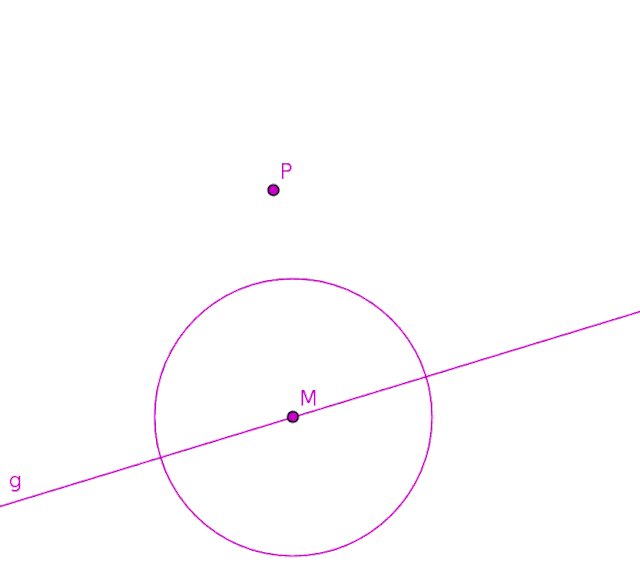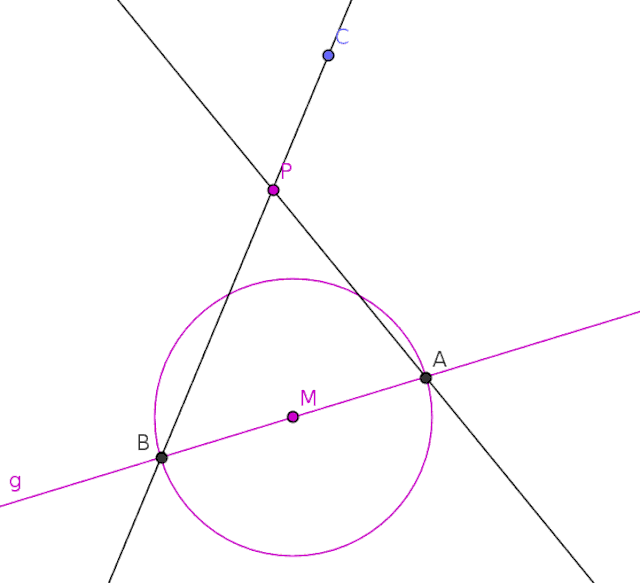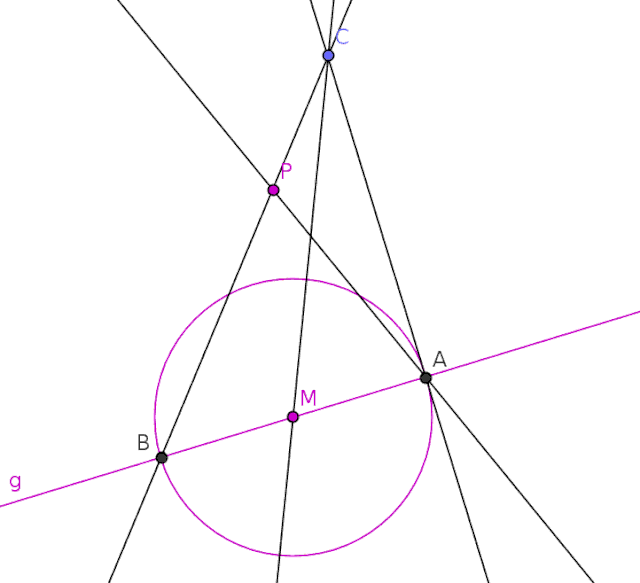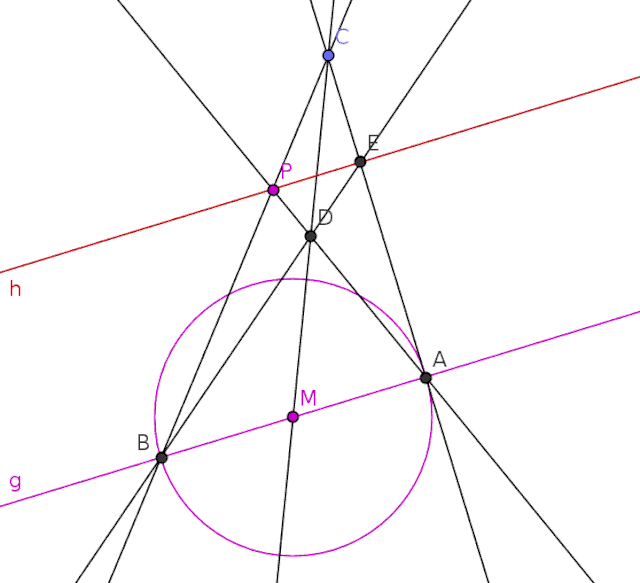
Gegeben sind auf einer Geraden g der Kreisdurchmesser AB mit seinem Mittelpunkt M und ein beliebiger Punkt P.

1. Zunächst ziehe eine gerade Linie durch die Punkte B und P.
2. Bestimme nach Belieben den Punkt C auf der geraden Linie.
3. Ziehe eine gerade Linie durch die Punkte A und P.
4. Ziehe eine gerade Linie durch die Punkte A und C.
5. Ziehe eine gerade Linie durch die Punkte M und C, es ergibt sich der Schnittpunkt D.
6. Ziehe eine gerade Linie durch die Punkte B und D, es ergibt sich der Schnittpunkt E.
7. Ziehe eine gerade Linie durch die Punkte E und P, somit ergibt sich die gesuchte Parallele zur Geraden g.

• Aus der nebenstehenden Konstruktion ist gut erkennbar (neben den vorgegebenen Punkten A und B ist kein weiterer Punkt auf dem Kreis), dass z. B. für eine Lösung der Aufgabe Eine Parallele zu einer Geraden durch einen beliebigen Punkt ziehen, der Kreis nicht erforderlich ist. Die Vorgabe eine Gerade mit den drei Punkten A, M und B von denen der Punkt M in deren Mitte liegt, ist nach Steiner ausreichend.^[2]

Von einem beliebigen Punkt ein Lot auf die Mittelachse eines Kreises fällen bzw. eine Senkrechte darauf errichten

Gegeben ist die Mittelachse eines Kreises mit dem Durchmesser AB, im Folgenden mit „Mittelachse AB“ bezeichnet, und ein beliebiger Punkt P.

• beliebiger Punkt P soll heißen, der Punkt P darf auch innerhalb des Kreises, auf dem Kreis sowie auf der Mittelachse AB des Kreises sein.

• Zwei mögliche Positionen des Punktes P sind konstruktiv berücksichtigt:

a) Punkt P mit ausreichendem Abstand zu einer zusätzlichen Mittelachse, die senkrecht zur ersten stehen soll, im Folgenden mit „zweite Mittelachse“ bezeichnet, um die Konstruktion mit deren Hilfe (z. B. JD) übersichtlich fortsetzen zu können; beschrieben in Variante 1 (Var. 1).

b) Punkt P ist zu nahe an einer zweiten Mittelachse, um die Konstruktion mit deren Hilfe übersichtlich fortsetzen zu können; beschrieben in Variante 2 (Var. 2).

Variante 1:
Von einem beliebigen Punkt ein Lot auf die Mittelachse eines Kreises fällen bzw. eine Senkrechte darauf errichten.
Punkt P mit ausreichendem Abstand zur anfangs virtuellen zweiten Mittelachse;
siehe 4 Beispiele als Animationen

Die Konstruktion beinhaltet drei Bausteine.

• Eine Parallele zur gegebenen Strecke AB.
• Eine Senkrechte zu der soeben gezeichneten Parallelen

a) als zweite Mittelachse des Kreises in Var. 1

b) als Senkrechte innerhalb des Kreises in Var. 2.

• Eine Parallele zu der soeben gezeichneten Senkrechten vom gegebenen Punkt P bis zur Mittelachse AB oder, wenn der Punkt P auf der Mittelachse AB des Kreises liegt, eine Parallele durch den bzw. ab dem Punkt P.

Variante 1 und Variante 2

Variante 2:
Von einem beliebigen Punkt ein Lot auf die Mittelachse eines Kreises fällen bzw. eine Senkrechte darauf errichten.
Punkt P zu nahe an der virtuellen zweiten Mittelachse;
siehe 4 Beispiele als Animationen

1. Zunächst bestimme auf dem Kreis nach Augenmaß den Punkt E mit BE ≈ Kreisradius (Winkel BME ≈ 60°). Ein Winkel BME von ca. 55° bis ca. 70° ist hilfreich für eine gut verwendbare Position des späteren Schnittpunktes J bzw. C in Var. 2.
2. Ziehe eine gerade Linie ab dem Punkt A durch den Punkt E.
3. Ziehe eine gerade Linie ab dem Punkt B durch den (in Var. 2 bis) Punkt E.
4. Bestimme nach Belieben den Punkt F auf der geraden Linie A durch E.
5. Verbinde den Punkt B mit F.
6. Verbinde den Punkt M mit F, es ergibt sich der Schnittpunkt G.
7. Ziehe eine gerade Linie ab dem Punkt A durch den Punkt G bis zur Strecke BF, es ergibt sich der Schnittpunkt H.
8. Ziehe eine gerade Linie ab dem Punkt H durch den Punkt E bis zum Kreis, es ergibt sich der Schnittpunkt I bzw. C in Var. 2. Die Strecke HI, bzw. HC in Var. 2, ist nach Steiner eine Parallele zum Kreisdurchmesser AB.^[2]

Fortsetzung Variante 1 (Punkt P mit ausreichendem Abstand zur anfangs virtuellen zweiten Mittelachse des Kreises)

9. Ziehe eine gerade Linie ab dem Punkt A durch den Punkt I, es ergibt sich der Schnittpunkt J.
10. Ziehe eine gerade Linie ab dem Punkt J durch den Punkt M bis zum Kreis, es ergeben sich die Schnittpunkte C und D. Die zweite Mittelachse JD ist nun die Hilfssenkrechte für die noch zu bestimmende parallele Senkrechte.

Fortsetzung Variante 2 (Punkt P ist zu nahe an der virtuellen zweiten Mittelachse des Kreises, um die Konstruktion übersichtlich fortsetzen zu können)

9. Ziehe eine gerade Linie ab dem Punkt E durch den Punkt M bis zum Kreis, es ergibt sich der Schnittpunkt D.
10. Verbinde den Punkt D mit C, es ergibt sich der Schnittpunkt M₁. Die Strecke DC ist die Hilfssenkrechte für die noch zu bestimmende parallele Senkrechte.

Fortsetzung Variante 1 und Variante 2

11. Ziehe eine gerade Linie ab dem Punkt C durch den Punkt P.
12. Bestimme nach Belieben den Punkt K auf der geraden Linie.
13. Verbinde den Punkt D mit K.
14. Verbinde den Punkt D mit P.
15. Verbinde den Punkt M, bzw. M₁ in Var. 2, mit K, es ergibt sich der Schnittpunkt L.
16. Ziehe eine gerade Linie ab dem Punkt C durch den Punkt L bis zur Strecke DK, es ergibt sich der Schnittpunkt N.
17. Ziehe eine gerade Linie so, dass die Punkte P und N darauf liegen.

Die damit erreichbaren Ergebnisse sind von der Position des gegebenen Punktes P abhängig.

Ergebnisse

a) P liegt nicht auf der Mittelachse AB: Das gesuchte Lot hat seinen Fußpunkt P' auf der Mittelachse AB.

b) P liegt auf der Mittelachse AB: Die gesuchte Senkrechte zur Mittelachse AB verläuft durch den Punkt P. Sie ist in Var.1 eine Parallele zur zweiten Mittelachse JD bzw. in Var.2 eine Parallele zur Hilfssenkrechten CD.

Quadratische Gleichung

Lösung der quadratischen Gleichung x² - px + q = 0

• Auflösung einer quadratischen Gleichung durch bloßes Ziehen von geraden Linien bei Benutzung eines gezeichneten Kreises.^[3]

Gegeben sei die Gleichung x² - px + q = 0; darin sind p und q rationale Zahlen.

Die darin eingezeichneten Parabel ist nicht Teil der Konstruktion, sie dient lediglich der Verdeutlichung.

1. Ziehe in einem kartesischen Koordinatensystem den Kreisbogen k mit Radius gleich 1 um den Mittelpunkt M(0|1).
2. Zeichne die zueinander parallelen Tangenten an den Punkten A(0|2) und B(0|0) ein.
3. Bestimme auf den entsprechenden Tangenten die Punkte C(${\displaystyle \mathrm {\tfrac {4}{p}} }$|2) und D(${\displaystyle \mathrm {\tfrac {q}{p}} }$|0).
4. Verbinde den Punkt C mit D, auf dem Kreisbogen k entstehen die Schnittpunkte E und F.
5. Ziehe abschließend die beiden geraden Linien ab Punkt A durch E und F, sie liefern auf der x-Achse die Punkte X₁ und X₂.

Die Längen |BX₁| = x₁ und |BX₂| = x₂ entsprechen den beiden Lösungen der quadratischen Gleichung x² - px + q = 0.

Siehe auch

• Linealgeometrie

Einzelnachweise

1. Jakob Steiner: Die geometrischen Konstructionen, ausgeführt mittelst der geraden Linie und Eines festen Kreises, als Lehrgegenstand auf höheren Unterrichts-Anstalten und zur praktischen Benutzung. Ferdinand Dümmler, Berlin 1833 (google.de [abgerufen am 2. April 2013]).
2. Jakob Steiner: Die geometrischen Konstructionen, ausgeführt mittelst der geraden Linie und Eines festen Kreises, als Lehrgegenstand auf höheren Unterrichts-Anstalten und zur praktischen Benutzung. Hrsg.: Ferdinand Dümmler. Berlin 1833 (ETH-Bibliothek, II Konstructionen mittels Lineal unter gewissen Voraussetzungen [Seite 14 §. 6.] S. 15, Aufgabe I. siehe auch Tafel I, Fig.3 [abgerufen am 20. September 2016]).
3. August Adler: Theorie der geometrischen Konstruktionen. G. J. Göschensche Verlagshandlung, Leipzig 1906, V. Abschnitt, Aufgaben ersten und zweiten Grades., §32. Graphische Auflösung der Gleichungen zweiten Grades., S. 175–176, Fig. 137., S. 188–189 (Textarchiv – Internet Archive).