Kugelkoordinaten

Kugelkoordinaten oder räumliche Polarkoordinaten sind orthogonale Koordinaten, in denen ein Punkt im dreidimensionalen Raum durch seinen Abstand vom Ursprung und zwei Winkel angegeben wird.

Übliche Darstellung der Kugelkoordinaten mit Radius ρ, Zenitwinkel θ und Azimut φ.

Bei Punkten auf einer Kugeloberfläche (Sphäre) um den Koordinatenursprung ist der Abstand vom Kugelmittelpunkt konstant. Dann sind nur noch die beiden Winkel variabel, sie werden dann als sphärische Koordinaten oder Kugelflächenkoordinaten^[1][2] bezeichnet.

Der Begriff „Kugelkoordinaten“ kann als Oberbegriff für den allgemeinen Fall und die sphärischen Koordinaten angesehen werden. Kugelkoordinaten sind wie Zylinderkoordinaten eine Verallgemeinerung der ebenen Polarkoordinaten auf den dreidimensionalen euklidischen Raum. Sie lassen sich auch weiter auf Räume beliebiger endlicher Dimension verallgemeinern.

Definitionen und Formeln

Übliche Konvention

Ein Kugelkoordinatensystem im dreidimensionalen euklidischen Raum wird festgelegt durch die Wahl

• eines Zentrums ${\displaystyle O}$ (Ursprung),
• einer gerichteten Gerade durch das Zentrum (Polachse), die die Polrichtung (oder Zenitrichtung) angibt, und durch diese festgelegt die Äquatorebene, die orthogonal zur Polrichtung durch das Zentrum verläuft, und
• einer Bezugsrichtung in der Äquatorebene.

Oft wird gleichzeitig ein kartesisches Koordinatensystem verwendet. Dann wird typischerweise der Ursprung des kartesischen Koordinatensystems als Zentrum gewählt, die z-Achse als Polachse (und damit die x-y-Ebene als Äquatorebene) und die x-Achse als Bezugsrichtung.

In der Version der Kugelkoordinaten, die in der Mathematik und in der Physik üblich ist, wird ein Punkt ${\displaystyle P}$ durch die folgenden drei Koordinaten festgelegt:

• ${\displaystyle r}$ oder ${\displaystyle \rho }$, der Radius, ist der Abstand des Punktes ${\displaystyle P}$ von ${\displaystyle O}$, hiermit wird die Kugeloberfläche festgelegt, auf der sich ${\displaystyle P}$ befindet.
• ${\displaystyle \theta }$ oder ${\displaystyle \vartheta }$,^[3] der Polarwinkel oder Poldistanzwinkel,^[4] ist der Vertikalwinkel zwischen der Polrichtung und der Strecke ${\displaystyle OP}$, gezählt von ${\displaystyle 0}$ bis ${\displaystyle \pi }$ (0° bis 180°), hierdurch wird der Ort des Punktes ${\displaystyle P}$ auf eine Kreislinie der Kugeloberfläche festgelegt.
• ${\displaystyle \varphi }$ oder ${\displaystyle \phi }$,^[3] der Azimutalwinkel,^[4] ist der Horizontalwinkel zwischen der Bezugsrichtung und der Orthogonalprojektion der Strecke ${\displaystyle OP}$, gezählt von ${\displaystyle -\pi }$ bis ${\displaystyle \pi }$ (−180° bis 180°) oder von ${\displaystyle 0}$ bis ${\displaystyle 2\pi }$ (0° bis 360°) gegen den Uhrzeigersinn. Hierdurch wird der Ort des Punktes ${\displaystyle P}$ auf der Kreislinie eindeutig definiert.

Die nachfolgende Abbildung zeigt einen Punkt ${\displaystyle P}$ mit den Kugelkoordinaten ${\displaystyle (r,\theta ,\varphi )}$. Die beiden Winkelgrößen ${\displaystyle \theta }$ und ${\displaystyle \varphi }$ werden auch als Winkelkoordinaten bezeichnet.

Umrechnungen

Kugelkoordinaten ${\displaystyle r,\theta ,\varphi }$ eines Punktes ${\displaystyle P}$ und kartesisches Koordinatensystem mit den Achsen ${\displaystyle x,y,z}$.

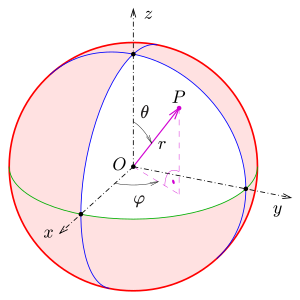
Jedem Koordinatentripel ${\displaystyle (r,\theta ,\varphi )}$ wird ein Punkt im dreidimensionalen euklidischen Raum zugeordnet (Parametrisierung). Wählt man ein kartesisches Koordinatensystem wie oben, so kann die Zuordnung durch die folgenden Gleichungen beschrieben werden:

${\displaystyle {\begin{array}{cll}x&=&r\cdot \sin \theta \cdot \cos \varphi \\y&=&r\cdot \sin \theta \cdot \sin \varphi \\z&=&r\cdot \cos \theta \end{array}}}$

Bei diesen Gleichungen können für ${\displaystyle r}$, ${\displaystyle \theta }$ und ${\displaystyle \varphi }$ beliebige Zahlenwerte eingesetzt werden. Damit die Kugelkoordinaten eindeutig bestimmt sind, muss man den Wertebereich der Koordinaten einschränken. Üblicherweise wird der Radius ${\displaystyle r}$ auf nichtnegative Werte beschränkt, der Winkel ${\displaystyle \theta }$ auf das Intervall ${\displaystyle [0,\pi ]}$ bzw. [0, 180°] und der Winkel ${\displaystyle \varphi }$ entweder auf das Intervall ${\displaystyle (-\pi ,\pi ]}$ bzw. (−180°, 180°] oder das Intervall ${\displaystyle [0,2\pi )}$ bzw. [0, 360°). Auch dann gibt es ausgeartete Punkte, für die die Winkelkoordinaten nicht eindeutig sind. Für Punkte auf der z-Achse ist der Winkel ${\displaystyle \varphi }$ nicht festgelegt, also beliebig. Für den Ursprung ist auch ${\displaystyle \theta }$ beliebig. Um Eindeutigkeit zu erreichen, kann man für diese Punkte ${\displaystyle \varphi =0}$ festlegen und für den Ursprung zusätzlich ${\displaystyle \theta =0}$.

Für die anderen Punkte lassen sich die Kugelkoordinaten ${\displaystyle (r,\theta ,\varphi )}$ aus den kartesischen Koordinaten ${\displaystyle (x,y,z)}$ durch die folgenden Gleichungen berechnen:^[5]

${\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}$

${\displaystyle \theta =\arccos \left({\frac {z}{r}}\right)}$

${\displaystyle \varphi =\operatorname {arctan2} (x,y)}$

Mit der arctan2-Funktion wird ein Winkel im Bogenmaß zwischen ${\displaystyle -\pi }$ und ${\displaystyle \pi }$ berechnet. Es gilt:

${\displaystyle \operatorname {arctan2} (x,y)={\begin{cases}\arctan \left({\frac {y}{x}}\right)&{\text{, wenn }}x>0,\\{\frac {\pi }{2}}\operatorname {sgn} y&{\text{, wenn }}x=0,\\\arctan \left({\frac {y}{x}}\right)+\pi &{\text{, wenn }}x<0\land y\geq 0,\\\arctan \left({\frac {y}{x}}\right)-\pi &{\text{, wenn }}x<0\land y<0.\end{cases}}}$

Andere Konventionen

Die obige Koordinatenwahl ist internationaler Konsens in der theoretischen Physik. Manchmal werden die Zeichen ${\displaystyle \theta }$ und ${\displaystyle \varphi }$ aber im umgekehrten Sinne verwendet, insbesondere in der amerikanischen Literatur.

Der Zenitwinkel ${\displaystyle \theta }$ ist nicht die geographische Breite, sondern lässt sich mit der Kobreite identifizieren. Die geographische Breite ist der Winkel zwischen der Äquatorialebene und dem Ortsvektor und nimmt Werte zwischen ${\displaystyle -90^{\circ }}$ und ${\displaystyle 90^{\circ }}$ an. Wird sie mit ${\displaystyle \phi }$ bezeichnet, so ist ${\displaystyle \phi =90^{\circ }-\theta ,\theta =90^{\circ }-\phi }$. Hingegen kann man das oben benutzte ${\displaystyle \varphi }$ ohne weiteres mit der geographischen Länge ${\displaystyle \lambda }$ östlich von Greenwich gleichsetzen (siehe geographische Koordinaten).

In der Darstellung mit dem Koordinatentripel ${\displaystyle (r,\phi ,\varphi )}$ und mit

${\displaystyle x=r\cos \phi \,\cos \varphi }$

${\displaystyle y=r\cos \phi \,\sin \varphi }$

${\displaystyle z=r\sin \phi \quad }$

entspricht ${\displaystyle \phi }$ der geographischen Breite.

Die Umrechnung der kartesischen Koordinaten eines Punktes ${\displaystyle P(x,y,z)}$ in die Winkelbestandteile erfolgt dann mit

${\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}$

${\displaystyle \theta =\arcsin \left({\frac {z}{r}}\right)}$

${\displaystyle \varphi =\operatorname {arctan2} (x,y).}$

Anwendungen

Kugelkoordinaten werden oft bei der Untersuchung von Systemen verwendet, die rotationssymmetrisch bezüglich eines Punktes sind. Beispiele sind: Volumenintegrale über Kugeln, die Beschreibung und Untersuchung rotationssymmetrischer Kraftfelder, wie z. B. das Gravitationsfeld eines kugelförmigen Himmelskörpers, das elektrische Feld einer Punktladung oder einer geladenen Kugel (siehe Beispiele zum Oberflächenintegral). Die betrachteten Größen hängen dann nicht von den Winkelkoordinaten ab, was viele Formeln vereinfacht. Wichtige partielle Differentialgleichungen wie die Laplace-Gleichung oder die Helmholtzgleichung können in Kugelkoordinaten durch Separation der Variablen gelöst werden.

Koordinatenlinien und Koordinatenflächen

Aus der Koordinatentransformation als Vektorgleichung mit dem Ortsvektor ${\displaystyle {\vec {r}}}$

${\displaystyle {\vec {r}}={\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}r\sin \theta \cos \varphi \\r\sin \theta \sin \varphi \\r\cos \theta \end{pmatrix}}}$

ergeben sich

• die Koordinatenlinien, indem man jeweils zwei der drei Koordinaten ${\displaystyle (r,\theta ,\varphi )}$ fest lässt und die dritte den Kurvenparameter darstellt
• die Koordinatenflächen, indem man eine der drei Koordinaten ${\displaystyle (r,\theta ,\varphi )}$ fest lässt und die beiden anderen die Fläche parametrisieren.

Für Kugelkoordinaten sind die Koordinatenlinien durch den Punkt ${\displaystyle (r_{0}\mid \theta _{0}\mid \varphi _{0})}$

• für den Parameter ${\displaystyle r}$ eine Halbgerade, die im Koordinatenursprung beginnt
• für den Parameter ${\displaystyle \theta }$ ein Halbkreis („Meridian“) mit dem Koordinatenursprung als Mittelpunkt und Radius ${\displaystyle r_{0}}$
• für den Parameter ${\displaystyle \varphi }$ ein Kreis („Breitenkreis“) mit Radius ${\displaystyle r_{0}\sin \theta _{0}}$ senkrecht zur z-Achse.

Als Koordinatenfläche durch den Punkt ${\displaystyle (r_{0}\mid \theta _{0}\mid \varphi _{0})}$ ergibt sich

• für konstanten Radius ${\displaystyle r_{0}}$ eine Kugelfläche mit dem Koordinatenursprung als Mittelpunkt
• für festen Winkel ${\displaystyle \theta _{0}}$ eine Kegeloberfläche mit der Spitze im Ursprung und der Polachse als Kegelachse, die für ${\displaystyle \theta _{0}=\pi /2}$ zu einer Ebene durch den „Äquator“ wird und für ${\displaystyle \theta _{0}=0}$ zu einer Geraden durch den „Nordpol“ und für ${\displaystyle \theta _{0}=\pi }$ zu einer Geraden durch den „Südpol“ entartet
• für konstanten Wert von ${\displaystyle \varphi _{0}}$ eine Halbebene mit der Polachse als Rand.

Zwei unterschiedliche Koordinatenflächen durch einen Punkt schneiden sich in einer Koordinatenlinie. Koordinatenlinien und Koordinatenflächen dienen dazu, die lokalen Basisvektoren zu berechnen. In der Tensorrechnung unterscheidet man wegen ihres unterschiedlichen Verhaltens bei Koordinatentransformationen zwischen kovarianten und kontravarianten Basisvektoren:

• die kovarianten Basisvektoren an einem Punkt sind jeweils tangential zu den Koordinatenlinien gerichtet
• die kontravarianten Basisvektoren an einem Punkt stehen jeweils senkrecht auf den Koordinatenflächen.

Transformation von Differentialen

Jacobi-Matrix

Die lokalen Eigenschaften der Koordinatentransformation werden durch die Jacobi-Matrix beschrieben. Für die Transformation von Kugelkoordinaten in kartesische Koordinaten lautet diese

${\displaystyle J={\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}={\begin{pmatrix}\sin \theta \cos \varphi &r\cos \theta \cos \varphi &-r\sin \theta \sin \varphi \\\sin \theta \sin \varphi &r\cos \theta \sin \varphi &r\sin \theta \cos \varphi \\\cos \theta &-r\sin \theta &0\end{pmatrix}}.}$

Die zugehörige Funktionaldeterminante lautet:

${\displaystyle \det J=r^{2}\sin \theta }$

Man berechnet die Jacobi-Matrix der entgegengesetzten Transformation am einfachsten als Inverse von ${\displaystyle J}$:

${\displaystyle J^{-1}={\frac {\partial (r,\theta ,\varphi )}{\partial (x,y,z)}}={\begin{pmatrix}\sin \theta \cos \varphi &\sin \theta \sin \varphi &\cos \theta \\{\frac {1}{r}}\cos \theta \cos \varphi &{\frac {1}{r}}\cos \theta \sin \varphi &-{\frac {1}{r}}\sin \theta \\-{\frac {1}{r}}{\frac {\sin \varphi }{\sin \theta }}&{\frac {1}{r}}{\frac {\cos \varphi }{\sin \theta }}&0\end{pmatrix}}.}$

Einige Komponenten dieser Matrix sind Brüche, an deren Nennern man die Uneindeutigkeit der Polarkoordinaten bei ${\displaystyle \textstyle r=0}$ und bei ${\displaystyle \textstyle \sin \theta =0}$ (also ${\displaystyle \textstyle \theta =0}$ oder ${\displaystyle \textstyle \pi }$) erkennt. Weniger gebräuchlich ist die Darstellung in kartesischen Koordinaten:

${\displaystyle J^{-1}={\begin{pmatrix}{\frac {x}{r}}&{\frac {y}{r}}&{\frac {z}{r}}\\\\{\frac {xz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {yz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {-(x^{2}+y^{2})}{r^{2}{\sqrt {x^{2}+y^{2}}}}}\\\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}.}$

Differentiale, Volumenelement, Flächenelement, Linienelement

Die Jacobi-Matrix erlaubt es, die Umrechnung von Differentialen übersichtlich als lineare Abbildung zu schreiben:

${\displaystyle {\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}=J\cdot {\begin{pmatrix}\mathrm {d} r\\\mathrm {d} \theta \\\mathrm {d} \varphi \end{pmatrix}}}$

beziehungsweise

${\displaystyle {\begin{pmatrix}\mathrm {d} r\\\mathrm {d} \theta \\\mathrm {d} \varphi \end{pmatrix}}=J^{-1}\cdot {\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}.}$

Das Volumenelement ${\displaystyle \mathrm {d} V=\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z}$ lässt sich besonders einfach mit Hilfe der Funktionaldeterminante

${\displaystyle \det J=r^{2}\sin \theta }$

umrechnen:

${\displaystyle \,\mathrm {d} V=r^{2}\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} \theta \,\mathrm {d} r.}$

Durch Differentiation ${\displaystyle {\frac {\mathrm {d} V}{\mathrm {d} r}}}$ erhält man für das Flächenelement ${\displaystyle \mathrm {d} A}$ auf einer Sphäre mit Radius ${\displaystyle r}$

${\displaystyle \mathrm {d} A=r^{2}\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} \theta .}$

Das Linienelement ${\displaystyle \mathrm {d} s}$ errechnet man gemäß

${\displaystyle \mathrm {d} s^{2}=\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2}=\mathrm {d} r^{2}+r^{2}\mathrm {d} \theta ^{2}+r^{2}\sin ^{2}\theta \mathrm {d} \varphi ^{2}}$

Metrik und Rotationsmatrix

Im Fehlen gemischter Glieder im Linienelement ${\displaystyle \mathrm {d} s}$ spiegelt sich wider, dass der metrische Tensor

${\displaystyle g=J^{T}J={\begin{pmatrix}1&0&0\\0&r^{2}&0\\0&0&r^{2}\sin ^{2}\theta \end{pmatrix}}}$

auch in Kugelkoordinaten keine Außerdiagonalelemente hat.

Der metrische Tensor ist offensichtlich das Quadrat der Diagonalmatrix

${\displaystyle h=\operatorname {diag} (1,r,r\sin \theta ).}$

Mit Hilfe dieser Matrix lässt sich die Jacobi-Matrix als ${\displaystyle J=Sh}$ schreiben, wobei ${\displaystyle S}$ die Rotationsmatrix

${\displaystyle S={\begin{pmatrix}\sin \theta \cos \varphi &\cos \theta \cos \varphi &-\sin \varphi \\\sin \theta \sin \varphi &\cos \theta \sin \varphi &\cos \varphi \\\cos \theta &-\sin \theta &0\end{pmatrix}}}$

ist.

Transformation von Vektorfeldern und -Operatoren

Im Folgenden soll die Transformation von Vektoren und Differentialoperatoren exemplarisch dargestellt werden. Die Ergebnisse werden bevorzugt in kompakter Form unter Benutzung von Transformationsmatrizen geschrieben. Die allermeisten Aussagen und Formeln gelten nur für Punkte außerhalb der z-Achse, für die die Jacobi-Determinante ungleich null ist.

Transformation der Vektorraumbasis

Kugelkoordinaten mit zugehöriger vom Ort abhängigen Orthogonalbasis ${\displaystyle \mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }}$

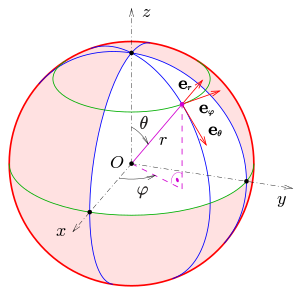
Der Basisvektor ${\displaystyle \mathbf {e} _{\varphi }}$ zur Koordinate ${\displaystyle \varphi }$ gibt an, in welche Richtung sich ein Punkt ${\displaystyle P(r,\theta ,\varphi )}$ bewegt, wenn die Koordinate ${\displaystyle \varphi }$ um einen infinitesimalen Betrag ${\displaystyle d\varphi }$ verändert wird:

${\displaystyle \mathbf {e} _{\varphi }\sim {\frac {\partial \mathrm {P} }{\partial \varphi }}={\frac {\partial x}{\partial \varphi }}\mathbf {e} _{x}+{\frac {\partial y}{\partial \varphi }}\mathbf {e} _{y}+{\frac {\partial z}{\partial \varphi }}\mathbf {e} _{z}.}$

Daraus erhält man

${\displaystyle \mathbf {e} _{\varphi }\sim {\frac {\partial \mathrm {P} }{\partial \varphi }}=-r\sin \theta \sin \varphi \mathbf {e} _{x}+r\sin \theta \cos \varphi \mathbf {e} _{y}.}$

Um eine orthonormale Basis zu erhalten, muss ${\displaystyle e_{\varphi }}$ noch auf die Länge ${\displaystyle 1}$ normiert werden:

${\displaystyle \mathbf {e} _{\varphi }=-\sin \varphi \,\mathbf {e} _{x}+\cos \varphi \,\mathbf {e} _{y}.}$

Auf gleiche Weise erhält man die Basisvektoren ${\displaystyle e_{r}}$ und ${\displaystyle e_{\theta }}$:

${\displaystyle \mathbf {e} _{r}=\sin \theta \cos \varphi \,\mathbf {e} _{x}+\sin \theta \sin \varphi \,\mathbf {e} _{y}+\cos \theta \,\mathbf {e} _{z}}$

${\displaystyle \mathbf {e} _{\theta }=\cos \theta \cos \varphi \,\mathbf {e} _{x}+\cos \theta \sin \varphi \,\mathbf {e} _{y}-\sin \theta \,\mathbf {e} _{z}}$

Als Spaltenvektoren geschrieben:

${\displaystyle \mathbf {e} _{r}={\begin{pmatrix}\sin \theta \cos \varphi \\\sin \theta \sin \varphi \\\cos \theta \end{pmatrix}},\qquad \mathbf {e} _{\theta }={\begin{pmatrix}\cos \theta \cos \varphi \\\cos \theta \sin \varphi \\-\sin \theta \end{pmatrix}},\qquad \mathbf {e} _{\varphi }={\begin{pmatrix}-\sin \varphi \\\cos \varphi \\0\end{pmatrix}}}$

Diese Basisvektoren bilden in der Reihenfolge ${\displaystyle \mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }}$ ein Rechtssystem.

Die zugehörigen Richtungen werden auch radial, meridional und azimutal genannt. Diese Begriffe spielen nicht nur in der Astronomie und den Geowissenschaften (z. B. Geographie, Geologie oder Geophysik) eine zentrale Rolle, sondern auch in Mathematik, Physik und verschiedenen Ingenieurwissenschaften, etwa bei der Ausstrahlung von elektromagnetischen Wellen („Hertzscher Dipol“) durch eine in z-Richtung aufgespannte Antenne, wo die Ausstrahlung in radialer Richtung erfolgt, während elektrisches bzw. magnetisches Feld in meridionaler bzw. azimutaler Richtung schwingen.

Mithilfe der oben eingeführten Rotationsmatrix ${\displaystyle S}$ lassen sich die Transformationen auch kompakt darstellen:

${\displaystyle (\mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi })=(\mathbf {e} _{x},\mathbf {e} _{y},\mathbf {e} _{z})\cdot S}$ .

In die Gegenrichtung lauten die Gleichungen dann:

${\displaystyle (\mathbf {e} _{x},\mathbf {e} _{y},\mathbf {e} _{z})=(\mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi })\cdot S^{T}.}$

Dabei wird verwendet, dass ${\displaystyle S}$ orthogonal ist und deshalb ${\displaystyle S^{-1}=S^{T}}$.

Transformation eines Vektorfeldes

Ein Vektor, als ein geometrisches Objekt, muss vom Koordinatensystem unabhängig sein:

${\displaystyle A_{x}\mathbf {e} _{x}+A_{y}\mathbf {e} _{y}+A_{z}\mathbf {e} _{z}=\mathbf {A} =A_{r}\mathbf {e} _{r}+A_{\theta }\mathbf {e} _{\theta }+A_{\varphi }\mathbf {e} _{\varphi }.}$

Diese Bedingung wird erfüllt durch

${\displaystyle {\begin{pmatrix}A_{x}\\A_{y}\\A_{z}\end{pmatrix}}=S\cdot {\begin{pmatrix}A_{r}\\A_{\theta }\\A_{\varphi }\end{pmatrix}}}$   beziehungsweise   ${\displaystyle {\begin{pmatrix}A_{r}\\A_{\theta }\\A_{\varphi }\end{pmatrix}}=S^{T}\cdot {\begin{pmatrix}A_{x}\\A_{y}\\A_{z}\end{pmatrix}}.}$

Transformation der partiellen Ableitungen

Die partiellen Ableitungen transformieren sich wie die Basisvektoren, aber ohne Normierung. Man kann genau wie oben rechnen, nur lässt man den Punkt ${\displaystyle P}$ im Zähler weg (tatsächlich werden in der modernen Formulierung der Differentialgeometrie die Koordinatenbasisvektoren des Tangentialraums und die partiellen Ableitungen gleichgesetzt) und verwendet die Jacobi-Matrix ${\displaystyle J=Sh}$ anstelle der Rotationsmatrix ${\displaystyle S}$. Die Transformation lautet also:

${\displaystyle \left({\frac {\partial }{\partial r}},{\frac {\partial }{\partial \theta }},{\frac {\partial }{\partial \varphi }}\right)=\left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right)\cdot J,}$

und in die Gegenrichtung

${\displaystyle \left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right)=\left({\frac {\partial }{\partial r}},{\frac {\partial }{\partial \theta }},{\frac {\partial }{\partial \varphi }}\right)\cdot J^{-1}.}$

Transformation des Nabla-Operators

Der Nabla-Operator ${\displaystyle \nabla }$ hat nur in kartesischen Koordinaten die einfache Form

${\displaystyle \mathbf {\nabla } =\mathbf {e} _{x}{\frac {\partial }{\partial x}}+\mathbf {e} _{y}{\frac {\partial }{\partial y}}+\mathbf {e} _{z}{\frac {\partial }{\partial z}}.}$

Sowohl die partiellen Ableitungen als auch die Einheitsvektoren muss man in der oben hergeleiteten Weise transformieren. Man findet:

${\displaystyle \mathbf {\nabla } =\mathbf {e} _{r}{\frac {\partial }{\partial r}}+\mathbf {e} _{\theta }{\frac {1}{r}}{\frac {\partial }{\partial \theta }}+\mathbf {e} _{\varphi }{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \varphi }}.}$

In dieser Form kann der transformierte Nabla-Operator unmittelbar angewandt werden, um den Gradienten eines in Kugelkoordinaten gegebenen Skalarfeldes zu berechnen.

Um die Divergenz eines in Kugelkoordinaten gegebenen Vektorfeldes A zu berechnen, ist hingegen zu berücksichtigen, dass ${\displaystyle \nabla }$ nicht nur auf die Koeffizienten ${\displaystyle A_{r},A_{\theta },A_{\varphi }}$ wirkt, sondern auch auf die in A implizit enthaltenen Basisvektoren ${\displaystyle \mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }}$

${\displaystyle \mathbf {\nabla } \cdot \mathbf {A} ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}(r^{2}A_{r})+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta A_{\theta })+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \varphi }}A_{\varphi }.}$

Um die Rotation eines in Kugelkoordinaten gegebenen Vektorfeldes A zu berechnen, ist dasselbe zu berücksichtigen:

${\displaystyle \mathbf {\nabla } \times \mathbf {A} ={1 \over r\sin \theta }\left({\partial \over \partial \theta }(A_{\varphi }\sin \theta )-{\partial A_{\theta } \over \partial \varphi }\right)\mathbf {e} _{r}+{1 \over r}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \varphi }-{\partial \over \partial r}(rA_{\varphi })\right)\mathbf {e} _{\theta }+{1 \over r}\left({\partial \over \partial r}(rA_{\theta })-{\partial A_{r} \over \partial \theta }\right)\mathbf {e} _{\varphi }.}$

Transformation des Laplace-Operators

Wenn man in der Divergenzformel als Vektorfeld A den Gradientenoperator ${\displaystyle \nabla }$ einsetzt, findet man den Laplace-Operator

${\displaystyle \mathbf {\Delta } =\mathbf {\nabla } ^{2}={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}}$

bzw.

${\displaystyle \mathbf {\Delta } ={\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}}{\partial \theta ^{2}}}+{\frac {1}{r^{2}}}{\frac {\cos \theta }{\sin \theta }}{\frac {\partial }{\partial \theta }}+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}.}$

Verallgemeinerung auf n-dimensionale Kugelkoordinaten

Eine Verallgemeinerung der Kugelkoordinaten auf ${\displaystyle n}$ Dimensionen:

${\displaystyle {\begin{aligned}x_{1}&=r\cos(\phi _{1})\\x_{2}&=r\sin(\phi _{1})\cos(\phi _{2})\\x_{3}&=r\sin(\phi _{1})\sin(\phi _{2})\cos(\phi _{3})\\&{}\,\,\,\vdots \\x_{n-1}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\\x_{n}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})\end{aligned}}}$

Die Winkel entwickeln sich nach:

${\displaystyle {\begin{aligned}\tan(\phi _{n-1})&={\frac {x_{n}}{x_{n-1}}}\\\tan(\phi _{n-2})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}}}{x_{n-2}}}\\&{}\,\,\,\vdots \\\tan(\phi _{1})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{2}}^{2}}}{x_{1}}}\end{aligned}}}$

Durch Umnummerierung erhält man eine Rekursionsformel für die Winkel:

${\displaystyle {\begin{aligned}x_{n}&=r\cos(\phi _{n-1})\\x_{n-1}&=r\sin(\phi _{n-1})\cos(\phi _{n-2})\\x_{n-2}&=r\sin(\phi _{n-1})\sin(\phi _{n-2})\cos(\phi _{n-3})\\&{}\,\,\,\vdots \\x_{2}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\sin(\phi _{1})\end{aligned}}}$

Woraus sich die folgenden Winkel ergeben:

${\displaystyle \left\Vert {\vec {L}}_{k}\right\Vert =\operatorname {sgn}(x_{k}){\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}={\frac {x_{k}}{\left\Vert x_{k}\right\Vert }}{\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}}$

mit ${\displaystyle \left\Vert {\vec {L}}_{0}\right\Vert =0}$ und

${\displaystyle \tan(\phi _{k})={\frac {\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}{x_{k+1}}}={\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}}$

Der Radius ist:

${\displaystyle r=\left\Vert {\vec {L}}_{n}\right\Vert }$

Eine Fallunterscheidung liefert mittels Arkustangens den passenden Winkel zur gegebenen kartesischen Koordinate, wobei ${\displaystyle \arctan(\pm \,\infty )=\pm \,{\tfrac {\pi }{2}}}$:

${\displaystyle {\begin{aligned}\phi _{k}={\begin{cases}\arctan \left({\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}\right)+\pi ,&{\text{(1) wenn: }}x_{k+1}<0\;\land \;k=n-1\\\arctan \left({\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}\right),&{\text{(2) wenn: }}{\text{nicht (1)}}\land \;{\text{nicht (3)}}\\0,&{\text{(3) wenn: }}x_{k+1}=\left\Vert {\vec {L}}_{k}\right\Vert =0\\\end{cases}}\end{aligned}}}$

Dabei fällt auf, dass ${\displaystyle {\begin{aligned}{\vec {L}}_{k}\end{aligned}}}$ immer ein zweidimensionaler Vektor ist für ${\displaystyle {\begin{aligned}k>0\end{aligned}}}$.

Jacobi-Matrix

Die Jacobi-Matrix der Kugelkoordinaten lautet bezüglich der als oberes gegebenen Nummerierung:

${\displaystyle J=\left({\begin{matrix}\cos(\phi _{1})&-r\sin(\phi _{1})&0&0&\cdots &0\\\sin(\phi _{1})\cos(\phi _{2})&r\cos(\phi _{1})\cos(\phi _{2})&-r\sin(\phi _{1})\sin(\phi _{2})&0&\cdots &0\\\vdots &\vdots &\ddots &\ddots &\ddots &\vdots \\\vdots &\vdots &\ddots &\ddots &\ddots &0\\\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})&r\cos(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})&\cdots &\cdots &\cdots &-r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})\\\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})&r\cos(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})&\cdots &\cdots &\cdots &r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\end{matrix}}\right)}$

Ihre Determinante beträgt:

${\displaystyle \det J_{(n)}=r^{n-1}\sin(\phi _{1})^{n-2}\sin(\phi _{2})^{n-3}\cdots \sin(\phi _{n-2})=\displaystyle r^{n-1}\cdot \prod _{k=2}^{n-1}\left(\sin(\phi _{n-k})\right)^{k-1}\quad n\geq 2}$

Das Integral über den Betrag dieser Determinante lässt sich mit der Gammafunktion ${\displaystyle \Gamma }$ angeben.

${\displaystyle \int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }\dots \int _{0}^{\pi }|\det J_{(n)}|\,{\text{d}}\phi _{1}\dots {\text{d}}\phi _{n-2}{\text{d}}\phi _{n-1}{\text{d}}r={\frac {2\pi R^{n}}{n}}\cdot \prod _{k=2}^{n-1}\int _{0}^{\pi }(\sin(\phi _{n-k}))^{k-1}{\text{d}}\phi _{n-k}={\frac {2\pi R^{n}}{n}}\cdot \prod _{k=2}^{n-1}{\frac {{\sqrt {\pi }}\;\Gamma \left({\frac {k}{2}}\right)}{\Gamma \left({\frac {k+1}{2}}\right)}}={\frac {{\sqrt {\pi }}^{n}R^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}}\quad n\geq 2}$

Dies entspricht dem Kugelvolumen einer ${\displaystyle n}$-dimensionalen Hyperkugel:

${\displaystyle V_{n}(R)={\frac {{\sqrt {\pi }}^{n}R^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}}}$

Beispiele

2D:

${\displaystyle \int _{0}^{R}\int _{0}^{2\pi }r\mathrm {d} \phi _{1}\mathrm {d} r=\pi R^{2}}$

3D:

${\displaystyle \int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }r^{2}\sin(\phi _{2}){\text{d}}\phi _{2}{\text{d}}\phi _{1}{\text{d}}r={\frac {4\pi R^{3}}{3}}}$

4D:

${\displaystyle \int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }\int _{0}^{\pi }r^{3}\sin ^{2}(\phi _{1})\sin(\phi _{2}){\text{d}}\phi _{1}{\text{d}}\phi _{2}{\text{d}}\phi _{3}{\text{d}}r={\frac {\pi ^{2}R^{4}}{2}}}$

Beispiel

Zuordnung am Beispiel ${\displaystyle n=3}$ mit den geläufigen Koordinatenachsen ${\displaystyle x,y,z}$:

${\displaystyle {\begin{aligned}x_{3}&=z=r\cos(\phi _{2})\\x_{2}&=x=r\sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=y=r\sin(\phi _{2})\sin(\phi _{1})\\\end{aligned}}}$

Die Winkel sind dann:

${\displaystyle {\begin{aligned}\tan(\phi _{2})={\frac {\left\Vert {\vec {L}}_{2}\right\Vert }{x_{3}}}&={\frac {\sqrt {x_{2}^{2}+x_{1}^{2}}}{x_{3}}}={\frac {\sqrt {x^{2}+y^{2}}}{z}}\\\tan(\phi _{1})={\frac {\left\Vert {\vec {L}}_{1}\right\Vert }{x_{2}}}&={\frac {\sqrt {x_{1}^{2}}}{x_{2}}}={\frac {y}{x}}\end{aligned}}}$

Literatur

• W. Werner: Vektoren und Tensoren als universelle Sprache in Physik und Technik. Band 1. Springer Vieweg, ISBN 978-3-658-25271-7.

Weblinks

• Matroids Matheplanet: Einführung in die Vektoranalysis (als PDF) von Eckard Specht

Einzelnachweise

1. Richard Doerfling: Mathematik für Ingenieure und Techniker. Oldenbourg Verlag, Seite 169.
2. F. W. Schäfke: Einführung in die Theorie der speziellen Funktionen der mathematischen Physik. Springer, 1963, ISBN 978-3-642-94867-1, Seite 129.
3. Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Band 3: Vektoranalysis, Wahrscheinlichkeitsrechnung, mathematische Statistik, Fehler- und Ausgleichsrechnung. 4. verbesserte Auflage. Vieweg + Teubner, Wiesbaden 2001, ISBN 3-528-34937-9.
4. Zylinder- und Kugelkoordinaten. (Memento vom 17. Dezember 2012 im Internet Archive). (PDF; 59 kB). Skript an der TU München.
5. Kugelkoordinaten. Mathematik-Online-Lexikon der Universität Stuttgart.