Diskussion:HSV-Farbraum/Archiv

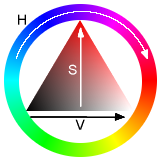
Thumb — Im Uhrzeigersinn. Dreieck ist falsch koloriert

Die Grafik oben rechts ist etwas merkwürdig. Die Farbe im Dreieck sollte doch die sein, auf die die eine Spitze des Dreiecks zeigt, oder? Also entweder, das Dreieck gehört gedreht, so dass es auf Rot unten rechts zeigt, oder die Farbe im Dreieck sollte geändert werden. --RokerHRO 15:54, 19. Sep 2004 (CEST)

Obige Aussage ist imho völlig richtig, kann das einmal jemand ändern? --(ohne unterschrift)

Am besten der, der die Grafik gemalt hat? ;-) --RokerHRO 16:33, 3. Feb 2005 (CET)

Stimme ebenfalls zu, dass die Grafik falsch ist... außerdem: gibt es eine "gesetzlich vorgeschriebene" Definition vom HSV-Farbraum? Z.B, ob der Farbton-Winkel mathematisch positiv (= gegen Uhrzeigersinn) oder negativ (= mit Uhrzeigersinn) verläuft? Diesem Artikel folgend, sowie GIMP würde ich schließen, dass der Winkel im Uhrzeigersinn verläuft. Wurde das in einer Norm gefestigt, z.B. von CIE oder ISO? Bildformate müssen ja auch miteinander kompatibel sein.

Außerdem: Schaut euch noch mal die Bilder an: bei dem einen dreht sich alles im Uhrzeigersinn, beim anderen gegen den uhrzeigersinn (auch die Farben sind "gespiegelt")... das wirkt sehr verwirrend für die meisten Leser m.E. Ich finde persönlich das Gegen-Uhrzeigersinn besser, da dies in der Mathematik auch so typisch ist. Aber ich überlasse das den DTP-Experten. Bitte meldet euch, und sagt, was der allgemeine Standard ist in Photoshop & Co.

--Abdull 00:31, 21. Mär 2005 (CET)

Ich habe unter http://roker.dingens.org/wikipedia/ ein Bildschirmfoto von dem Farbkreis von Gimp abgespeichert. vielleicht kann daraus ja jemand der maltechnisch mehr drauf hat als ich, daraus was machen. :-) --RokerHRO 16:27, 21. Mär 2005 (CET)

Hallo alle miteinander. Also meines Wissens hat Smith (1978) den HSV Raum als Pyramide mit sechseckiger Grundfläche dargestellt. Die Darstellung als Kegel ist falsch und mathematisch nicht korrekt. Es wird hier irreführend, meines erachtens, der Parameter S als Horizontale Achse gezeigt. Dies ist ebenfalls nicht korrekt.

Kann mal einer dazu Stellung nehmen, ich würd den Artikel dann auch komplett überarbeiten!--Moquai 17:29, 14. Apr 2005 (CEST)

Die Darstellung der Farben im HSV-Modell als auf der Spitze stehender Kegel ist m.E. unbefriedigend, trägt dies doch in keiner Weise der Tatsache Rechnung, dass natürlich die sekundärfarben (cyan, magenta und gelb) logischerweise eine größere maximale Helligkeit erreichen als die drei Primärfarben (rot, grün und blau), da sie ja selbst additive Mischungen von je 2 Primärfarben sind; ganz zu schweigen von weiß als additiver Mischung aller 3 Primärfarben. --Slow Phil 11:39, 28. Apr 2005 (CEST)

Hallo Slow Phil! Tut mir leid, aber ich verstehe hier Dein Problem nicht. Das geht schon damit los, daß Du hier irgendwas mit den Primär- und Sekundärfarben durcheinanderwirfst: Welche genau als solche bezeichnet werden, ist nämlich vom verwendeten Farbmodell abhängig (beim HSV-System gibt es GARKEINE) – dafür gibt es keine einheitliche Definition (da ja, wie man beim CIE-Normvalenzsystem sieht, eben NICHT jede Farbe durch drei andere ermischt werden kann). Weiterhin verstehe ich nicht, warum denn die Mischfarben zwingend heller sein müßten, als die reinen Farben – hier geht es doch nicht darum, wieviel Strahlungsintensität man mit einzelnen Lichtquellen aufsummieren kann, sonderen doch eher, wie hell eine momochromatische (Spektral-)Farbe einer bestimmten Intensität (oder auch Energie) letztlich wirkt. Und drittens bezieht sich Deine Kritik wohl eher auf das HSV-System, als auf die Beschreibung dessen in diesem Artikel – und selbstverständlich HAT dieses Sysytem einige Schwächen, aber dafür kann doch der Autor nichts?! Gruß, Torge, alias --DiplomBastler 07:56, 5. Mai 2005 (CEST)

hat er die achsen verwechselt? sollte waagerechte achse nicht die sättigung sein, steht doch nen dickes S dran, oder beschriftung der grafik ist falsch

Hallo zusammen,

wenn HSV und HLS schon in einem Artikel abgehandelt werden, sollte wenigstens auf die geometrischen Unterschiede der Systeme eingegangen werden. HLS hat je nach Darstellungsart die Form eines Doppelkegels bzw. eines Zylinders. "Schwarz" und "Weiß" sitzen dann je nach Darstellungsart an den Kegelspitzen bzw. auf Grund- und Deckfläche. Bei HSV sitzt "Weiß" im Mittelpunkt der Kegelgrundfläche.

Siehe dazu auch: http://edoc.hu-berlin.de/e_rzm/17/schnabel-gisela-1999-02-01-a/HTML/8.html

Meine Motivation: Für einige Algorithmen ist HLS einfach vorteilhafter. Gibt es eigentlich eine genormte HLS-RGB-Transformation? Neben der im Artikel erwähnten (Tektronix) ist mir bei meinen Recherchen noch eine weitere Definition über den Weg gelaufen: http://isgnw2.cs.uni-magdeburg.de/~regina/CG1_VL11.pdf

Grüße ...

-- Breitbandkatze 00:42, 21. Mai 2005 (CEST)

siehe auch englische wikipedia http://en.wikipedia.org/wiki/HLS_color_space#Comparison_of_HSL_and_HSV -- 17.01.2006

Was noch bedeutend ist, ist die verschiedene Umrechnung von RGB zu HSL bzw. zu HSV. Siehe engl. Wikipedia Seite. Die erklärt es richtig. H ist bei beiden gleich, die beiden anderen Parameter verschieden.

HSV : V = MAX; S = (MAX-MIN) / MAX;

HSL : L = (MAX+MIN) / 2; S = (MAX-MIN)/ 2L wenn L <= 1/2; S = (MAX - MIN)(2-2L) wenn L > 1/2

Wobei HSL auch HSI heißt. Windows in seinen Farbdialogen benutzt den HSL Algorithnus. Norbert

Fehler in der Formel?

Hallo,

Die Formeln auf der englischen Seite sind anders als die auf der Deutschen. Ich habe den angegebenen Algorithmus implementiert und der Algorithmus auf der Englischen Seite gibt die gleichen Werte wie der Farbauswahldialog im Photoshop zurück (ja, kein Beweis für Richtigkeit, aber ein Indiz). Das ist bei dem Algorithmus der deutschen Seite nicht so.

Grüße

Die Formel zur Umrechnung von HSV zu RGB ist zumindest für den Wert V falsch. Bei vielen anderen Quellen wird angegeben, dass V einfach nur dem maximalen Farbwert entspricht. Daher gehe ich davon aus, dass der Fehler hier zu finden ist. --Stultissimum 20:50, 13. Mai 2006 (CEST)

fragt sich aber, was der unterschied zu der in Grauwert angegeben formel ist

Grauwert = 0,299·Rot + 0,587·Grün + 0,114·Blau

das eine ist wohl ein farbmetrischer Value, das andre ein photometrischer wert Brightness, mir fehlt aber gerade der Fachausdruck

auch hab ich die formeln ergänzt und auf die in der einleitung angegeben %-einteilung umgestellt --W!B: 10:48, 17. Mai 2006 (CEST)

PS kann noch wer nachrechnen, ob H > 360° sein kann, dann fehlt noch eine normierung bei if H<0

Die obige Formel für den Grauwert gibt die Helligkeit einer Farbe so an, wie sie der Mensch wahrnimmt (grün als hellste Farbe, blau als dunkelste). Die "Helligkeits-Angabe" beim HSV-Modell hat meines Wissens nichts mit der Helligkeit Y (des YUV-Modells) zu tun. Zumindest habe ich in Erinnerung, dass dies oft am HSV-Modell kritisiert wurde. Aber hier mag ich mich natürlich auch irren können. --Stultissimum 01:27, 1. Jun 2006 (CEST)

Beispiel für den Fehler

Ich habe auch den Algorithmus zuerst von der deutschen Seite implementiert, und mich gewundert warum er nicht funktioniert. Ein Beispiel für H=40°, V=100, S=50:

t= V*(100-(S*(1-f))) = V*(100-(S*(1-(H/60-Hk)))) = V*(100-(S*(1-(0.66)))) = V*(100-(S*(0.33))) = V * (100-16.66) = 100 * 83.33 = 8333

was ein viel zu hoher Wert ist, wenn man Zielbereiche für RGB von 0-100 annimmt. Ersetzt man die 100 durch 1 (wie auf der englischen Seite), und nimmt man 0 bis 1 als Bereich für S und V an, stimmts (Zielwerte für RGB von 0-1, welche sich leicht in was anderes umrechnen lassen). Gruß Martin

HSL NOT! = HSV

das ist der HSI raum nach Gonzalez and Woods (Quelle: HSI: Hue Saturation Intensity)

H' = arccos ( 2*R-G-B / (2*sqrt( (R-G)^2 + (R-B)*(G-B)) ) ) - in Bogenmaß, kann undefiniert sein, siehe unten

H = H' *180/π falls B < G, sonst H = 360° - H' *180/π

S = 100*( 1 - 3 * MIN(R,G,B)/(R+G+B) ) - kann undefiniert sein, siehe unten

V = 100*(R+G+B)/3

--W!B: 15:29, 30. Aug 2006 (CEST)

Die Definition ist FALSCH! (siehe oben #HLS != HSV)

HSV (Hue, Saturation, Value): Farbton (Farbwinkel), Farbsättigung, Dunkelstufe
- HSB (Hue, Saturation, Brightness): Farbton, Farbsättigung, Helligkeit
- HSL (Hue, Saturation, Luminance): Farbton, Farbsättigung, Leuchtdichte
- HSI (Hue, Saturation, Illuminance/Intensity): Farbton, Farbsättigung, Beleuchtungsstärke/Lichtintensität
  (alle redir hierher)
LCh-Farbraum (Lightness, Croma, Hue angle): Helligkeit (Farbe)/Farbhelligkeit, Buntheit, Bunttonwinkel

--W!B: 21:07, 9. Mai 2006 (CEST)

jetzt passts aber schon fast.. --W!B: 06:49, 15. Mai 2006 (CEST)

Grauwert für Value stimmt nicht: der Grauwert ist ein zum Buntton gleich helles Grau (wird verwendet bei der umwandlung eines Farbbildes in s/w), hier im HSV aber sind Weiß und Buntfarben "gleich hell", dürfte also dem NCS-Schwarzanteil und der DIN-Dunkelstufe entsprechen - wo wir diese begriffe klären, überlegen wir im Wikipedia:WikiProjekt Farbe -- W!B: 14:42, 14. Sep. 2007 (CEST)

Ich beschäftige mich gerade programmtechnisch mit Farben und Umrechnungen, wobei ich die hier genannten Formeln verwendet habe. Zur Kontrolle meines Programms benutze ich das Farbmisch-Tool von PaintShop Pro 6.02. Was mich jetzt verwirrt, ist die Tatsache, dass PSP die Helligkeit ganz anders berechnet, und zwar weder als Maximalwert von RGB noch als Mittelwert (R+G+B)/3, sondern folgendermaßen:

Ich beginne mit R=0, B=0, G=0, da ist H natürlich auch 0. Jetzt drehe ich Rot auf 255, dabei macht H jeden zweiten Schritt mit und landet bei 128. Nun drehe ich zusätzlich Grün auf bis 255, dabei bleibt H unverändert bei 128. Erst wenn ich auch noch Blau aufdrehe, klettert H von 128 auf 255.

An sich eine logische Sache: nur so kann H einen Unterschied zwischen Rot und Weiß darstellen, ohne aber einen Unterschied zwischen Rot und Gelb zu machen. Bloß: wie passt das zu dem Artikel? --Plenz 19:07, 11. Sep. 2007 (CEST)

ganz einfach: 1.4 Transformation von RGB und HSV - da kocht jeder sein süppchen, solang Du nicht an die tatsächlichen algorithmen des programms herankommst, keine chance: hierbei scheint sichs um einen satz auf das Doppelkegelmodell zu handeln -- W!B: 14:59, 13. Sep. 2007 (CEST)

Ehrlich gesagt, kapiere ich überhaupt nichts. OK, beim HSV-Modell scheint es mehrere "Dialekte" zu geben, aber was hat das mit den räumlichen Modellen zu tun? Das einzig sinnvolle Modell scheint mir sowieso der Kegel zu sein, weil da jede Farbe ihren festen Platz hat. Schon der Zylinder fällt dadurch auf, dass Schwarz überall auf der unteren Fläche sein kann, und wozu ein Doppelkegel gut sein soll, ist in der gesamten Wikipedia nicht zu ersehen (oder gut versteckt). --Plenz 17:45, 14. Sep. 2007 (CEST)

ach, wozu glaubst Du, gibt es etliche duzend farbräume? "Das einzig sinnvolle"..? jedes hat halt seinen zweck.. nachteil ist, dass weiß und bunt im HSV-system gleich "hell" (gleich weit vom schwarz entfernt) sind, das ist (für manche zwecke) patschert - beim doppelkegel (HSL) aber ist der farbkreis auf höhe eines graus - dass ein rot einem grau entspricht, nicht einem weiß, ist etwa bei der umwandlung in ein s/w-bild wesentlich angenehmer - sowas geht im HSV nicht gut, wenn Du S runterdrehst, landest Du bei weiß.. daher ist auch die umrechnung in RGB nicht so einfach (ich hab das auber noch explizit dazugeschrieben) in der Bildbearbeitung etwa zieht man das HSL oder LCh(Lab)-Modell vor, weils besser zu handhaben ist

den zylinder findest Du etwa (abgewickelt) in den standard-farbwählern im betriebsystem oder textverarbeitung, einfach, weil Du ein viereckiges kastel bekommst: bunt oben, unten alles schwarz, da wär HSB dem laien weniger zugänglich, der zylinder abgewickelt hätteoben alles weiß, unten alles schwarz und die buntfarben in der mitte (mir persönlich lieber..) - ein kegel lässt sich nicht abwickeln - es hat halt jedes system seine vor und nachteile.. -- W!B: 22:40, 14. Sep. 2007 (CEST)

PS und noch unter halboffenes Intervall nachschauen, bevor Du rumbastelst ;) .. ist das nicht irgendwann in der schule, so 2. klasse mittelschule? -- W!B: 22:46, 14. Sep. 2007 (CEST)

Nun gut - Streit beiseite. Ich möchte nur ergänzend anmerken, dass der Satz "Außerdem ist zu beachten, ob das zugrunde liegende Modell ein Würfel, eine Kugel, ein Kegel, Doppelkegel oder anderer Körper ist." dem Leser eher Verwirrung als Erkenntnis bringt, weil völlig unklar ist, was wie warum beachtet werden muss, und wenn man es beachtet, welche konkreten Konsequenzen zu ziehen sind. Außerdem ist so ein Begriff wie Doppelkegel schnell verlinkt - dumm nur, wenn der verlinkte Artikel nicht weiter aussagt. Sind die Doppelkegel jetzt über die Grundflächen oder über die Spitzen miteinander verbunden? --Plenz 21:11, 23. Sep. 2007 (CEST)

Sorry, aber unsere Lehrer haben sich glücklicherweise um das sinnentleerte Thema "Mengenlehre" herumgedrückt (und das sage ich als Bauingenieur). Meiner Meinung nach sollte man diesen Mathefuzzikram durch das jedermann verständliche "wobei R, G, und B Werte zwischen 0 und 1 (einschließlich) annehmen können" ersetzen. --Plenz 21:11, 23. Sep. 2007 (CEST)

versteh ich jetzt nicht, ist in #Varianten des Farbraumes eh erläutert und verlinkt.. und die erfahrung hat gezeigt, dass genau der satz mit [0,1] offenkudnig vielen leuten probleme bereitet, weil regelmässig auf irgendwelche andere intervalle umgestellt wird - obwohl die einleitung dahingehend eindeutig ist - ich denk, sie lesen einfach nicht, was da steht, wenns so kompliziert ist, dass sie nachdenken anfangen müssen, und den ganzen artikel lesen, statt gleich auf den formelsatz zu hupfen, wirds einfacher ;) -- W!B: 09:09, 24. Sep. 2007 (CEST)

{\begin{aligned}H&\in [0,360)\\S,I,R,G,B&\in [0,1]\end{aligned}}

H'=\arccos \left[{\frac {2R-G-B}{2{\sqrt {(R-G)^{2}+(R-B)(G-B)}}}}\right]

H={\begin{cases}H',&{\text{falls }}B<G\\360^{\circ }-H',&{\text{sonst}}\end{cases}}

S=1-3\cdot {\frac {\min(R,G,B)}{R+G+B}}

$I={\frac {1}{3}}(R+G+B)$
Beispiel für Transformation von RGB nach HSI

Gegeben sei R = 255, G = 255 und B = 0. Normiert auf 1 erhält man R = 1, G = 1 und B = 0

H=\arccos \left[{2\cdot 1-1-0 \over 2\cdot {\sqrt {(1-1)^{2}+(1-0)\cdot (1-0)}}}\right]=\arccos \left[{1 \over 2}\right]=60^{\circ }

S=1-3\cdot {\frac {\min(1,1,0)}{1+1+0}}=1-3\cdot {\frac {0}{2}}=1

I={\frac {1}{3}}(1+1+0)={\frac {2}{3}}

Der Farbton mit 100% Sättigung liegt bei 60°, was der Farbe gelb entspricht. Die Intensität beträgt 2/3.

von Akribix 2007-06-17 - nett, aber wir brauchen hier nicht etliche umrechnungsformel - also konkret angeben auf welches modell es sich bezieht, und imho ist das sowieso nur eine näherungsformel für I (pseudo-I) - und wie sind die 6 grundfarben auf den Kreis verteilt? -- W!B: 15:04, 13. Sep. 2007 (CEST)

ah, sehe schon, auch Gonzalez and Woods.. deren satz ist absichtlich nicht angegeben.. -- W!B: 15:58, 13. Sep. 2007 (CEST)

aus dem Artikel von hier übertragen.

Ich möchte euch einmal darauf hinweisen, dass man in diesem Artikel die kegelförmige Darstellung entfernen sollte und grundsätzlich die Zylindrische nehmen sollte, weil S (Sättigung) in der Regel eine gleichbleibende Bitbreite hat, sofern man nicht in JPEG komprimiert hat o.Ä..

durch --LKD 09:23, 15. Nov. 2007 (CET)

danke, wär nicht nötig gewesen, das hier zu deponieren.. -- W!B: 11:27, 15. Nov. 2007 (CET)

Also so wie das da steht, ist das V nicht in [0, 100] sondern in [0, 1] bzw r,g,b auch in [1, 100]

stimmt.. -- W!B: 00:57, 19. Nov. 2007 (CET)

Hi, wozu braucht man bei der Umrechnung HSV→RGB den Spezielfall S=0 (bzw. s=0)? Der ist offenbar im allgemeinen Fall enthalten, weil dann p=q=t=v wird. Das bläht die Formel lediglich auf. Rundungsfehler können der Grund auch nicht sein bei dem linearen Zeug... --Georg-Johann 11:05, 25. Mär. 2008 (CET)

Nun der (qualifizierte) Mensch mag ja diesen Trivialfall sofort erkennen und definieren das ein Punkt im dreidemensionalen Raum doch nur ein Punkt bleibt! Für ein automatisiertes Rechenprogramm ist es aber immer noch nötig auf einige Spezialfälle zuverweisen: trivial benannt sei die Anweisung wenn Du durch Null teilen sollst, dann führe die Aktion nicht aus, sondern setze dafür den Wert xyx ein. Deshalb werden hier so einige spezielle Fälle aus der Berechnung ausgenommen und für den Einzelfall definiert. Hinweis: diese Ausführungen sind nur ein Modell und gelten nur in diesen Grenzen. --Paule Boonekamp - eine Silbersonne 14:24, 25. Mär. 2008 (CET)

Ähhh... verzieh, wenn ich Dir grad net folgen kann. Ich sehe hier nur Divisionen durch 100 bzw. 60, und in besagtem Fall (S=0) eine Multiplikation mit Null. Ich find den Sonderfall immer noch überflüssig. Es ist ja keine stetige Fortsetzung oder sowas, sondern entspricht etwa der Definiton

f(x) = 0 für x=0 und f(x) = x für x ≠ 0

Der Grund für den Sonderfall liegt m.E. lediglich im englischen Original begründet, ist dort aber ebensowenig erhellend wie notwendig. --Georg-Johann 19:23, 25. Mär. 2008 (CET)

stimmt, scheint sich um eine computer-algorithmische abkürzung zu handeln - mathematisch ists unnötig - und ich frag mich schön langsam, ob wir die umrechnung nicht komplett raushauen, sie stiftet mehr verwirrung, als sie hilft, kommt sowieso immer was anderes raus als beim programm am heimischen computer - und ist daher quelle permanenter umbauten - vielleicht geben wir einfach nur die literatur an, kein mensch implementiert sowas heute noch selbst, und schon gar nicht nach vorgabe der WP.. -- W!B: 22:47, 26. Mär. 2008 (CET)

Falsch. Mir ist's gerade deshalb aufgefallen weil ich's implementiert hab *g*, genauso wie der Fehler mit dem "V anstatt v" in der Formel. Ich find's gut die Formeln anzugeben und habe sie auch dort gefunden, wo ich sie gesucht habe -- in der WP --Georg-Johann 23:14, 27. Mär. 2008 (CET)

oh ;) - na dann sag Du, lassen wir die exception drin, oder hauen wir sie raus? es ist ja zu betonen, das nur der HSV-Raum die undefinierten stellen hat (als polarkoordinatensystem-derivat), der RGB-raum ist eh stetig (karthesisch), also braucht die rückumwandung keine sonderregelungen.. -- W!B: 23:36, 27. Mär. 2008 (CET)

Umrechnung HSV in RGB

Welchen Zweck hat der Wert f in dieser Formel? Wenn ich für Schokobraun aus dem Artikel rechne, bekomme ich für $h_{\mathrm {i} }$ einen Wert von 0.4. Setzt man diesen in die Formel für f ein, kommt 0 heraus. Oder bedeuten die nicht ganz fertigen Klammern in der Formel $h_{\mathrm {i} }:=\left\lfloor {H \over 60^{\circ }}\right\rfloor$ dass auf die nächste ganze Zahl abgerundet wird? --Hartmetall (Diskussion) 20:42, 4. Nov. 2013 (CET)

Ja, dass ist eine Gauß-Klammer, siehe Abrundungsfunktion und Aufrundungsfunktion --84.170.157.216 02:32, 2. Dez. 2019 (CET)

Jeder Tuschkasten hat Braun mit dabei. Deswegen habe ich das mal mit in die Farbtabelle aufgenommen. Wikipedia ist für's Volk. Also auch "normale Alltagsfarben" einordnen ist sehr nützlich. ---Arno Nym (nicht signierter Beitrag von 80.149.148.212 (Diskussion) 16:00, 25. Mai 2012 (CEST))

An Arno Nymus

Du sprichst mir aus dem Herzen.

Ping willkommen, Steue (Diskussion) 16:47, 26. Aug. 2023 (CEST)

Das HSV-Modell ist wie die anderen Derivate kein Farbraum. Ein Farbraum ist definiert durch Primärvalenzen, die Koordinaten entweder im CIE xyY-Farbraum oder CIE XYZ-Farbraum haben. Weiter ist eine Farbraum definiert durch einen Weißpunkt (vorzugsweise aus der CIE D-Serie) und eine Transferfunktion (Gamma). (nicht signierter Beitrag von Eberhard Hasche (Diskussion | Beiträge) 09:00, 3. Jan. 2015 (CET))

Das stieß mir auch ziemlich auf - erstens ist schon der Seitentitel ("HSV-Farbraum") falsch, zweitens werden andere Farbmodelle ebenfalls als "Farbräume" bezeichnet. Aber auch das nicht konsistent - im Abschnitt "HSV-Raum und Farbwahrnehmung" ist dann plötzlich die Rede vom "HSV-Modell", das in Konkurrenz zu den Alternativen RGB und CMYK stehen soll (Korrekt wäre hier CMY; CMYK ist weder ein Farbraum noch ein -modell). --Mighty rearranger (Diskussion) 14:01, 2. Aug. 2024 (CEST)

Ich teile diese Kritik nicht. Im mathematischen Sinn ist ein Raum durch eine Menge von möglichst unabhängigen Variablen gegeben. Das HSV-Modell bietet ja tatsächlich eine einigermaßen anschauliche räumliche Vorstellung, gewissermaßen in Polarkoordinaten ausgedrückt. Es kann m.E. ruhig "Farbraum" heißen. Es hilft m.E. andererseits auch gar nichts, auf sprachlichen Feinheiten herumzureiten, das trägt nicht zu einem besseren Verständnis der Sache bei. Oder worin seht ihr mögliche Missverständnisse? --TiHa (Diskussion) 17:44, 2. Aug. 2024 (CEST)