Polární soustava souřadnic je taková soustava souřadnic v rovině , u které jedna souřadnice (označovaná
r
{\displaystyle r}
vzdálenost bodu od počátku souřadnic , druhá souřadnice (označovaná
φ
{\displaystyle \varphi }
úhel spojnice tohoto bodu a počátku od zvolené osy ležící v rovině (nejčastěji jí odpovídá osa
x
{\displaystyle x}
kartézských souřadnic ).
Tento článek potřebuje úpravy.
Tento článek není dostatečně
ozdrojován , a může tedy obsahovat informace, které je třeba
ověřit .
Polární soustava souřadnic je vhodná v případech takových pohybů , při nichž se nemění vzdálenost tělesa od jednoho bodu (počátku souřadnic), například u pohybu po kružnici , případně se tato vzdálenost mění s nějakou jednoduchou závislostí.
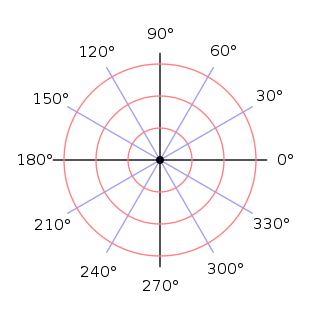
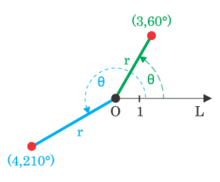
Souřadnicová síť v polárních souřadnicích Bod v polární soustavě souřadnic Ukázka dvou bodů v polárních souřadnicích: [r=3; φ=60°] a [r=4; φ=210°] Ukázka převodu polárních souřadnic [r; φ] na kartézské [x; y]
Transformace polárních souřadnic na kartézské :
x
=
r
cos
φ
{\displaystyle x=r\cos {\varphi }\,}
y
=
r
sin
φ
{\displaystyle y=r\sin {\varphi }\,}
Převod kartézských souřadnic na polární :
r
=
x
2
+
y
2
{\displaystyle r={\sqrt {x^{2}+y^{2}}}}
φ
=
arctg
(
y
x
)
{\displaystyle \varphi =\operatorname {arctg} \left({\frac {y}{x}}\right)}
Tato převodní funkce však funguje jen na intervalu
φ
∈
⟨
0
,
π
2
⟩
{\displaystyle \varphi \in \langle 0,{\frac {\pi }{2}}\rangle }
funkce arctg(x ) . Abychom mohli popsat inverzi pro daný úhel na celém jeho definičním intervalu , bývá často používána funkce arctg2(y ,x ) definovaná jako
arctg2
(
y
,
x
)
=
{
arctg
(
y
x
)
,
je-li
(
x
>
0
)
∧
(
y
>
0
)
,
arctg
(
y
x
)
+
π
,
je-li
(
x
<
0
)
,
arctg
(
y
x
)
+
2
π
,
je-li
(
x
>
0
)
∧
(
y
<
0
)
,
{\displaystyle \operatorname {arctg2} (y,x)=\left\{{\begin{matrix}\operatorname {arctg} \left({\frac {y}{x}}\right),\ \ \ \ \ \ &{\mbox{je-li }}(x>0)\wedge (y>0),\\\operatorname {arctg} \left({\frac {y}{x}}\right)+\pi ,\ &{\mbox{je-li }}(x<0),\ \ \ \ \ \ \ \ \ \ \ \ \ \\\operatorname {arctg} \left({\frac {y}{x}}\right)+2\pi ,&{\mbox{je-li }}(x>0)\wedge (y<0),\\\end{matrix}}\right.}
Převod kartézských souřadnic na polární má potom zápis:
r
=
x
2
+
y
2
{\displaystyle r={\sqrt {x^{2}+y^{2}}}}
φ
=
arctg2
(
y
,
x
)
{\displaystyle \varphi =\operatorname {arctg2} \left(y,x\right)}
Jedná se o ortogonální soustavu souřadnic s Lamého koeficienty
h
r
=
1
h
φ
=
r
{\displaystyle h_{r}=1\quad h_{\varphi }=r}
Délka infinitesimální úsečky se spočte jako
d
s
2
=
d
r
2
+
r
2
d
φ
2
,
{\displaystyle \mathrm {d} s^{2}=\mathrm {d} r^{2}+r^{2}\mathrm {d} \varphi ^{2},}
tedy délka křivky obecně jako
∫
t
1
t
2
(
d
r
(
t
)
d
t
)
2
+
r
2
(
d
φ
(
t
)
d
t
)
2
d
t
,
{\displaystyle \int _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {\mathrm {d} r(t)}{\mathrm {d} t}}\right)^{2}+r^{2}\left({\frac {\mathrm {d} \varphi (t)}{\mathrm {d} t}}\right)^{2}}}\mathrm {d} t,}
kde t je parametr dané křivky a s je její délka od
t
1
{\displaystyle t_{1}}
t
2
{\displaystyle t_{2}}
Obsah infinitesimálního elementu plochy spočteme jako
d
S
=
r
d
r
d
φ
,
{\displaystyle \mathrm {d} S=r\mathrm {d} r\mathrm {d} \varphi ,}
takže celkový obsah spočteme integrací tohoto výrazu přes danou oblast vyjádřenou v polárních souřadnicích.
Christofelovy koeficienty Levi-Civitovy konexe generované Euklidovskou metrikou jsou dány vztahy
Γ
r
r
r
=
Γ
φ
φ
φ
=
Γ
r
r
φ
=
Γ
r
φ
r
=
Γ
φ
r
r
=
0
{\displaystyle {\Gamma ^{r}}_{rr}={\Gamma ^{\varphi }}_{\varphi \varphi }={\Gamma ^{r}}_{r\varphi }={\Gamma ^{r}}_{\varphi r}={\Gamma ^{\varphi }}_{rr}=0}
Γ
φ
φ
r
=
Γ
φ
r
φ
=
1
r
{\displaystyle {\Gamma ^{\varphi }}_{\varphi r}={\Gamma ^{\varphi }}_{r\varphi }={\frac {1}{r}}}
Γ
r
φ
φ
=
−
r
{\displaystyle {\Gamma ^{r}}_{\varphi \varphi }=-r}
∇
f
=
∂
f
∂
r
r
^
+
1
r
∂
f
∂
φ
φ
^
{\displaystyle \nabla f={\partial f \over \partial r}{\boldsymbol {\hat {r}}}+{1 \over r}{\partial f \over \partial \varphi }{\boldsymbol {\hat {\varphi }}}}
∇
⋅
A
=
1
r
∂
(
r
A
r
)
∂
r
+
1
r
∂
A
φ
∂
φ
{\displaystyle \nabla \cdot \mathbf {A} ={1 \over r}{\partial \left(rA_{r}\right) \over \partial r}+{1 \over r}{\partial A_{\varphi } \over \partial \varphi }}
Δ
f
=
∇
2
f
=
1
r
∂
∂
r
(
r
∂
f
∂
r
)
+
1
r
2
∂
2
f
∂
φ
2
{\displaystyle \Delta f=\nabla ^{2}f={1 \over r}{\partial \over \partial r}\left(r{\partial f \over \partial r}\right)+{1 \over r^{2}}{\partial ^{2}f \over \partial \varphi ^{2}}}
Δ
A
=
(
Δ
A
r
−
A
r
r
2
−
2
r
2
∂
A
φ
∂
φ
)
r
^
+
(
Δ
A
φ
−
A
φ
r
2
+
2
r
2
∂
A
r
∂
φ
)
φ
^
{\displaystyle \Delta \mathbf {A} =\left(\Delta A_{r}-{A_{r} \over r^{2}}-{2 \over r^{2}}{\partial A_{\varphi } \over \partial \varphi }\right){\boldsymbol {\hat {r}}}+\left(\Delta A_{\varphi }-{A_{\varphi } \over r^{2}}+{2 \over r^{2}}{\partial A_{r} \over \partial \varphi }\right){\boldsymbol {\hat {\varphi }}}}
Obrázky, zvuky či videa k tématu polární soustava souřadnic na Wikimedia Commons 
