četnost 1. číslice v sadách číselných dat From Wikipedia, the free encyclopedia
Benfordův zákon, někdy též Newcombův-Benfordův zákon, je matematický zákon, který říká, že v mnoha souborech přirozených dat (ale ne ve všech) začínají čísla mnohem častěji číslicí 1 než jinou číslicí. Alternativní formulace: první číslice čísla pravděpodobně bude malá.[1] Zhruba 30 % čísel začíná jedničkou. Čím vyšší počáteční číslice je, tím méně pravděpodobně se vyskytuje na začátku čísel (viz obrázek s histogramem relativní četnosti výskytu jednotlivých číslice).
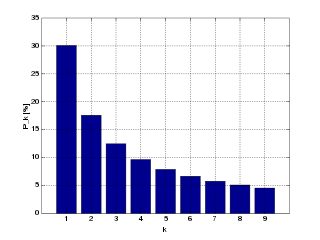
Ve skupině čísel reprezentujících reálné hodnoty čehokoli je asi 30% pravděpodobnost, že první číslovkou bude jednička. Dále pak 17,6 % čísel bude začínat dvojkou, 12,5 % trojkou a jen 4,57 % devítkou. Nejde o žádný matematický trik, ale o skutečný přírodní zákon, jímž se řídí soubory jakýchkoli přirozených dat bez ohledu na jejich podstatu nebo fyzikální jednotky. Jedinou podmínkou je, že data musí být v minimálním rozsahu tří logaritmických intervalů (tj. v minimálním rozsahu tří desítkových řádů).[2]
Tuto skutečnost poprvé objevil a zveřejnil kanadsko-americký matematik a astronom Simon Newcombe v článku „Note on the Frequency of Use of the Different Digits in Natural Numbers“ publikovaném v American Journal of Mathematics (1881, č. 4, s. 39–40).[3] Upozornil na skutečnost, že logaritmické tabulky v technické knihovně mají mnohem více ohmatané první stránky, tzn. stránky s čísly počínajícími jedničkou, než stránky na konci, tzn. stránky s čísly začínajícími číslicí 9. Usoudil, že uživatelé logaritmických tabulek (vědci a studenti přírodovědných a společenských oborů) se při své práci častěji setkávají s čísly začínajícími číslicí 1 nebo 2 než s čísly začínajícími číslicí 8 nebo 9. Na první pohled se zdá přirozené předpokládat, že první platná číslice čísel, s nimiž se lidé setkávají, bude se stejnou pravděpodobností jednička, dvojka i devítka. S touto intuitivní představou je však Newcombovo tvrzení v rozporu.[4]
Newcombe neuvedl žádnou analýzu konkrétních souborů dat, pokusil se však o určité matematické zdůvodnění výsledku. Článek upadl v zapomnění – autorovu tvrzení nebyla věnována pozornost několik desetiletí.[5]
Tento z určitého hlediska přírodní jev znovu objevil v roce 1938 fyzik Frank Benford.[5] Svá zjištění publikoval v článku „The Law of Anomalous Numbers“ v Proceedings Of The American Philosophical Society (1938, vol. 78, no. 4, s. 551–572).[6] Na rozdíl od Newcomba založil svá tvrzení na empirických pozorováních. Několik let shromažďoval číselné údaje z různých zdrojů a oborů (např. plochy povodí 335 řek, měrné skupenské teplo 1389 chemických sloučenin, čísla vyskytující se na titulní stránce novin a další). Dohromady zpracoval více než 20 000 číselných údajů ve 20 různých souborech dat a ukázal, že první číslice se opravdu nevyskytují všechny stejně často. I proto se pro zmíněnou zákonitost užívá pojmenování Benfordův zákon.[7][5]
Simon Newcomb i Frank Benford dospěli každý jinou cestou k vyjádření téhož.[7]
Počáteční číslice n () čísla v soustavě o základu b () se objevuje s pravděpodobností . V desítkové soustavě () dodržují počáteční číslice podle Benfordova zákona následující rozložení:
| 1 | 30,1 % |
| 2 | 17,6 % |
| 3 | 12,5 % |
| 4 | 9,7 % |
| 5 | 7,9 % |
| 6 | 6,7 % |
| 7 | 5,8 % |
| 8 | 5,1 % |
| 9 | 4,6 % |
První příklad: pokud prozkoumáme seznam 58 nejvyšších staveb na světě, potom jednička je zdaleka nejčetnější vedoucí číslice, dokonce bez ohledu na to, zda výšku těchto staveb vyjádříme v metrech nebo ve stopách – i když při vyjádření výšky staveb v metrech je relativní četnost jedničky výrazně vyšší než při vyjádření ve stopách (vit Tabulka 1).
Druhý příklad (zobrazený v grafu vpravo od tabulky 1) ukazuje aplikaci Benfordova zákona na čísla, která vyjadřují velikost populace jednotlivých zemí (použita jsou data pro 237 zemí z června 2010). Červené sloupce zobrazují relativní četnost (v procentech) pro jednotlivé číslice. Černé tečky (nad nebo uvnitř každého sloupce) ukazují, jaká by měla být výška sloupce, pokud by relativní četnosti byly přesně podle Benfordova zákona.

| První číslice |
metry | stopy | Dle Benfordova zákona | ||
|---|---|---|---|---|---|
| Počet | Podíl v % | Počet | Podíl v % | ||
| 1 | 24 | 41,4 % | 16 | 27,6 % | 30,1 % |
| 2 | 9 | 15,5 % | 8 | 13,8 % | 17,6 % |
| 3 | 7 | 12,1 % | 5 | 8,6 % | 12,5 % |
| 4 | 6 | 10,3 % | 7 | 12,1 % | 9,7 % |
| 5 | 1 | 1,7 % | 10 | 17,2 % | 7,9 % |
| 6 | 5 | 8,6 % | 4 | 6,9 % | 6,7 % |
| 7 | 1 | 1,7 % | 2 | 3,4 % | 5,8 % |
| 8 | 4 | 6,9 % | 5 | 8,6 % | 5,1 % |
| 9 | 1 | 1,7 % | 1 | 1,7 % | 4,6 % |
Třetí příklad ukazkuje četnost první číslice pro mocniny čísla dvě (2n). Pokud vezmeme sekvenci prvních číslic pro mocniny prvních 96 čísel (1, 2, 4, 8, 1, 3, 6, 1, 2, 5, 1, 2, 4, 8, 1, 3, 6, 1, ... , což je celočíselná Posloupnost A008952 v databázi On-Line Encyclopedia of Integer Sequences, relativní četnosti první číslice se opět výrazně blíží k hodnotám podle Benfordova zákona. Mnohem více, než bychom očekávali pro náhodnou posloupnost stejné délky, protože tato posloupnost prvních číslice je odvozena od geometrické posloupnosti druhých mocnin čísla dva.[8]
| První číslice |
Četnost | Dle Benfordova zákona | |
|---|---|---|---|
| Počet | v % | ||
| 1 | 29 | 30,2 % | 30,1 % |
| 2 | 17 | 17,7 % | 17,6 % |
| 3 | 12 | 12,5 % | 12,5 % |
| 4 | 10 | 10,4 % | 9,7 % |
| 5 | 7 | 7,3 % | 7,9 % |
| 6 | 6 | 6,3 % | 6,7 % |
| 7 | 5 | 5,2 % | 5,8 % |
| 8 | 5 | 5,2 % | 5,1 % |
| 9 | 5 | 5,2 % | 4,6 % |
Benfordův zákon lze aplikovat při jednoduchém testování regulérnosti voleb, odhalování účetních podvodů (vč. národních účtů), při analýze zaokrouhlovacích chyb při rozsáhlých numerických výpočtech, jako doplňkový test k dalším metodám zkoumání kvality makroekonomických dat aj.
Konkrétně u voleb není Benfordův zákon sám o sobě důkazem podvodu, ale vodítkem nebo indikací k tomu, že k němu mohlo dojít, přičemž někdy mohou být „anomálie“ vysvětleny. U statistických dat je potřeba, aby se vstupní údaje lišily o několik řádů k tomu, aby se chovaly podle Benfordova zákona. Konkrétně k aplikaci tohoto zákona jako pomůcky pro zjišťování volebních podvodů existuje vědecká práce z univerzity v Cambridge z roku 2011,[9] která mimo jiné říká: „Pokud dojde k vyrovnanému soupeření dvou kandidátů ve volebních okrscích s počtem voličů řádově mezi 100 až 1000 na okrsek, pak první číslice počtu hlasů u každého kandidáta nebudou 1 nebo 2, ale spíše 4, 5 nebo 6.“
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.