Projecció ortogonal

Una projecció ortogonal és, en geometria euclidiana, aquella en què les rectes projectants auxiliars són perpendiculars al pla de projecció, establint una relació entre tots els punts de l'element projectant amb els projectats.^[1][2][3][4]

La projecció ortogonal del segment AB sobre la recta L és el segment PQ .

En el pla, la projecció ortogonal és aquella les línies projectants auxiliars són perpendiculars a la recta de projecció L.^[5]

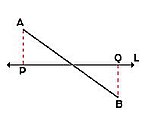
Així, donat un segment AB, n'hi haurà prou projectar els punts "extrems" del segment -mitjançant línies projectants auxiliars perpendiculars a L-, per determinar la projecció sobre la recta L.

Una aplicació de projeccions ortogonals són els teoremes de les relacions mètriques en el triangle mitjançant les quals es pot calcular la dimensió dels costats d'un triangle.

El concepte de projecció ortogonal es generalitza a espais euclidians de dimensió arbitrària, fins i tot de dimensió infinit. Aquesta generalització té un paper important en moltes branques de matemàtica i física.

Casos de projecció ortogonal en el pla

Projecció ortogonal d'un punt:

• La projecció ortogonal d'un punt P és un altre punt A situat a prop de L, que s'obté traçant una línia perpendicular a L des del punt A.

Projecció ortogonal d'un segment:

• Cas general: si el segment donat AB no és paral·lel a la recta L, la projecció ortogonal és segment PQ que s'obté traçant línies perpendiculars a L des dels punts extrems. La magnitud de la projecció sempre és menor que la del segment donat.

• Si el segment PQ i la recta L són paral·lels, la projecció serà: AB = PQ, que s'obté de forma anàloga.

• Si el segment AB té un punt comú amb la recta L, la projecció s'obté de manera similar.

• Si el segment AB talla a la recta L, la projecció s'obté de forma anàloga.

Vegeu també

Projecció gràfica	Projecció cònica Projecció paral·lela Projecció ortogonal Projecció obliqua

• Ortofotografia
• Ortofotomapa
• Perspectiva axonomètrica