Loading AI tools
من ويكيبيديا، الموسوعة الحرة
المتباينة[1]أو المتراجحة[1] (بالإنجليزية: Inequality) في الرياضيات، هي علاقة رياضية تعبّر عن اختلاف قيمة عنصرين رياضيين، وغالباً ما تحوي إحدى الرموز (> ، < ، ≥ ، ≤).
| صنف فرعي من | |
|---|---|
| التدوين الرياضي | |
| لديه جزء أو أجزاء | |
| النقيض |
في جميع الأمثلة السابقة المتغيران a وb غير متساويين. وتعرف هذه العلاقات بعلاقات اللامساواة الصارمة، وذلك بالمقارنة مع العلاقات التالية:
كما تستخدم المتباينات في تعريف الفترة -وهي نوع خاص من المجموعات الجزئية من الأعداد الحقيقية- ، وهناك ثلاث أنواع من الفترات تعرف كما يلي :
{a,b] = {x ∈ ℝ , a ≤ x ≤ b]
{a,b) = {x ∈ ℝ , a < x < b)
{a,b) = {x ∈ ℝ , a ≤ x < b]
حالات التعدي في المتراجحات:
لا تتغير جهة المتراجحة إذا تم جمع أو طرح من طرفيها نفس العدد,
فإذا كانت ثلاث أعداد حقيقية فإنه: إذا كان > فإنً >
لا تتغير جهة المتراجحة إذا ضربنا أو قسمنا طرفيها على نفس العدد الموجب المغاير للصفر.
تتغير جهة المتراجحة إذا ضربنا أو قسمنا طرفيها على نفس العدد السالب المغاير للصفر.
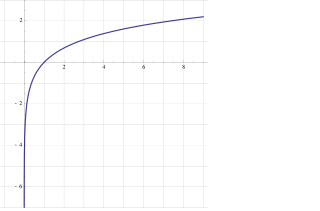
على سبيل المثال، تطبيق دالة اللوغارتم الطبيعي على طرفي المتباينة يعطي ما يلي:
بنفس طريقة حل المعادلات من الدرجة الأولى في مجهول واحد مع الأخذ في الاعتبار خصائص علاقة التباين وهي لا تختلف عن خصائص علاقة التساوي إلا في حالة الضرب والقسمة في عدد سالب حيث إن إشارة التباين في هذه الحالة تنعكس من أصغر إلى أكبر أو من أكبر إلى أصغر
12- > 4(2x+7)
12- > 28 + (x(8
12- 28- > (x(8
40- > (x(8
x < (-40)/8
x < -5
(8-) > (y(-2
y > 4
أنظر أيضا لائحة المتراجحات.
إذا كان x عددا حقيقيا، فإن القيمة المطلقة للعدد X ويرمز لها بالرمز |x| تعرف كالآتي:
على سبيل المثال فإن:
من التعريف السابق نجد أن القيمة المطلقة لأي عدد حقيقي x هو مقياس هذا العدد بصرف النظر عن إشارته. أي أن |x| > صفر دائماً.
إذا كان x|=y ,y>0|
فإن x=y أو x=-y
إذا كان x عددا حقيقيا أكبر من الصفر (x > 0) فإن:
x|<y ⇔ -y<x<y|
حيث ⇔ (إذا وفقط إذا) تعني أنه إذا تحقق الشرط يتحقق الجواب وإذا تحقق الجواب يتحقق الشرط أيضاً (علاقة من طرفين).
إذا كان x عددا حقيقيا أكبر من الصفر (x > 0) فإن:
x>y ⇔ |x|>y أو x<-y.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.