Rectangle

Un rectangle és un polígon quadrilàter del grup dels paral·lelograms^[1] tal que tots els seus angles són angles rectes. Es caracteritza del quadrat per no ser un polígon regular, o sigui, que no tots els seus costats són iguals (tenen la mateixa mida). Es pot considerar el quadrat com un cas concret de rectangle en què tots els seus costats tenen la mateixa longitud.

Rectangle de base 5 i altura 4. El seu perímetre és 18 i la superficie 20

El perímetre, L, d'un rectangle de base b i altura h és:

${\displaystyle L=2\cdot b+2\cdot h\,}$

L'àrea, també denominada com a superfície (S) d'un rectangle de base b i altura h és:

${\displaystyle S=b\cdot h\,}$

La revolució d'un rectangle a l'espai sobre qualsevol dels seus costats genera un cilindre.

El terme oblong es fa servir sovint per fer referència a rectangles que no són quadrats.^[2][3][4]

Caracteritzacions

Un quadrilàter convex és un rectangle si i només si compleix qualsevol de les següents característiques:^[5][6]

• un paral·lelogram amb almenys un angle recte
• un paral·lelogram amb diagonals d'igual longitud
• un paral·lelogram ABCD on els triangles ABD i DCA són congruents
• un quadrilàter equiangular
• un quadrilàter amb quatre angles rectes
• un quadrilàter les dues diagonals del qual són iguals en longitud i es biseccionen entre ells^[7]
• un quadrilàter convex amb costats successius a, b, c, d l'àrea del qual és ${\displaystyle {\tfrac {1}{4}}(a+c)(b+d)}$.^[8]:fn.1
• un quadrilàter convex amb costat successius a, b, c, d amb àrea ${\displaystyle {\tfrac {1}{2}}{\sqrt {(a^{2}+c^{2})(b^{2}+d^{2})}}.}$^[8]

Classificació

Un rectangle és un cas particular tant d'un paral·lelogram i d'un trapezi. Un quadrat és un cas particular d'un rectangle.

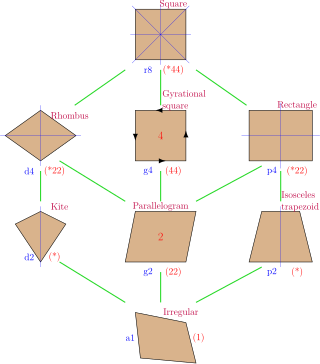
Jerarquia tradicional

Un rectangle és un cas particular d'un paral·lelogram en què cada parella d'arestes adjacents és perpendicular.

Un paral·lelogram és un cas particular d'un trapezi en què totes dues parelles de costats oposats són paral·lels i iguals en longitud.

Un trapezi és un quadrilàter convex que té com a mínim una parella de costats oposats paral·lels.

Un quadrilàter convex és

• Simple: la frontera no es creua amb si mateixa.
• Amb forma d'estrella: tot l'interior és visible des d'un sol punt, sense creuar cap aresta.

Jerarquia alternativa

De Villiers va definir el rectangle d'una manera més general com tot quadrilàter amb eixos de simetria a través de cada parella de costat oposats.^[9] Aquesta definició inclou tant els rectangles rectes com els creuats. Cadascun d'aquestes té un eix de simetria paral·lel a i equidistant a una parella de costats oposats, i un altre que és la bisectriu perpendicular d'aquests costats, però, en el cas del rectangle creuat, el primer eix no és un eix de simetria de cap dels costats que bisecciona.

Els quadrilàters amb dos eixos de simetria, cadascun d'ells a través d'una parella de costat oposats, pertanyen a la classe més gran de quadrilàters amb almenys un eix de simetria a través d'una parella de costats oposats. Aquests quadrilàters inclouen els trapezis isòsceles i els trapezis isòsceles creuats (quadrilàters creuats amb la mateixa disposició de vèrtexs que un trapezi).

Propietats

Rectangle ABCD. d és una de les dues diagonals.

1. Els seus costats paral·lels són iguals.
2. Les dues diagonals d'un rectangle de base ${\displaystyle b}$ i altura ${\displaystyle h}$ mesuren ${\displaystyle {\sqrt {a^{2}+h^{2}}}}$.^[10]
3. Les seves dues diagonals es bisequen mútuament en el punt mig comú; (aquesta característica també el defineix). Aquest punt és el centre de la figura, en el sentit que tota recta que passa per ell, tala al rectangle en dos punts equidistants del centre, per la qual cosa defineix una simetria respecte a un punt per als punts del rectangle.^[11]
4. El rectangle té dues simetries axials, respecte a eixos paral·lels als seus costats i que passen pel centre.^[12][13]
5. Qualsevol rectangle es pot inscriure en una circumferència, dos dels diàmetres del qual coincideixen amb les diagonals del rectangle.
6. Usant com a base d'un triangle una base del rectangle i el punt mig del costat oposat, com a vèrtex oposat, resulta un triangle isòsceles d'àrea igual a la meitat de la del rectangle.
7. Emprant com a base de qualsevol triangle la base del rectangle i com a vèrtex oposat un punt que dista com l'altura del rectangle, s'obté una família de triangles equivalents i els vèrtexs dels quals formen un lloc geomètric: la recta paral·lela a la base del rectangle.^[14]
8. Si s'uneixen els punts mitjans M, N; P, Q de sengles costats d'un rectangle, mitjançant segments es genera el rombe MNPQ.^[15]

Fórmules

Fórmula pel perímetre d'un rectangle

L'àrea d'un rectangle és el producte de la longitud i l'amplada.

Si un rectangle té longitud ${\displaystyle \ell }$ i amplada ${\displaystyle w}$, llavors:^[16]

• té àrea ${\displaystyle A=\ell w\,}$;
• té perímetre ${\displaystyle P=2\ell +2w=2(\ell +w)\,}$;
• cada diagonal té longitud ${\displaystyle d={\sqrt {\ell ^{2}+w^{2}}}}$; i
• quan ${\displaystyle \ell =w\,}$, el rectangle és un quadrat.^[17]

Dualitat rectangle-rombe

El polígon dual del rectangle és un rombe, com es mostra en la següent taula.^[18]

Rectangle	Rombe
Tots els angles són iguals.	Tots els costats són iguals.
Els costats oposats són iguals.	Els angles oposats són iguals.
El seu centre és equidistant als seus vèrtexs, per tant, té un circumcercle.	El seu centre és equidistant als seus costats, per tant té un incercle.
Els dos eixos de simetria biseccionen costats oposats.	Els dos eixos de simetria biseccionen angles oposats.
Les diagonals són iguals en longitud.	Les diagonals s'intersecten en angles iguals.

• La figura formada unint, en ordre, els punts mitjos dels costats d'un rectangle és un rombe i vice versa.

Teoremes

El teorema d'isoperimetría per a rectangles estableix que d'entre tots els rectangles amb un perímetre donat, el quadrat és el que té major àrea.

Un paral·lelogram amb diagonals iguals és un rectangle.

El punt mig dels costats de dos quadrilàters qualssevol amb diagonals perpendiculars formen un rectangle.

El teorema japonès per a quadrilàters cíclics^[19] afirma que els incentres dels quatre triangles determinats pels vèrtexs d'un quadrilàter cíclic agafats tres alhora formen un rectangle.

The teorema de la bandera britànica afirma que siguin els vèrtexs d'un rectangle anomenats A, B, C, i D, per tot punt P en el mateix pla que el rectangle:^[20]

${\displaystyle \displaystyle (AP)^{2}+(CP)^{2}=(BP)^{2}+(DP)^{2}.}$

A tot cos convex C en el pla, se li pot inscriure un rectangle r en C tal que una còpia homotètica R de r és circumscrita a C i la raó homotètica positiva és com a màcxim de 2 i ${\displaystyle 0.5{\text{ × Area}}(R)\leq {\text{Area}}(C)\leq 2{\text{ × Area}}(r)}$.^[21]

Existeix un únic rectangle amb costats ${\displaystyle a}$ i ${\displaystyle b}$, on ${\displaystyle a}$ és inferior a ${\displaystyle b}$, amb dues maneres de ser doblegat respecte d'una línia a partir del seu centre de tal manera que l'àrea de solapament sigui minimitzada i cada àrea dona una forma diferent – un triangle i un pentàgon. El ratio únic dels costats és ${\displaystyle \displaystyle {\frac {a}{b}}=0.815023701...}$.^[22]

Magnituds geomètriques per a un rectangle

Donada una figura bidimensional poden definir-se els n-moments d'àrea centrats com:

${\displaystyle M_{x_{1}\dots x_{n}}^{(n)}=\int _{A}x_{1}\dots x_{n}\ dA}$

El 0-moment coincideix amb l'àrea, els dos 1-moments s'anomenen primers moments d'àrea (o moments estàtics) ${\displaystyle \scriptstyle S_{x}=M_{x}^{(1)},\ S_{y}=M_{y}^{(1)}}$ són nuls per a qualsevol figura plana. Els 2-moments s'anomenen segons moments d'àrea (o moments d'inèrcia plans) i per a un rectàngle són:

${\displaystyle I_{xx}=M_{xx}^{(2)}={\frac {bh^{3}}{12}},\quad I_{yy}=M_{yy}^{(2)}={\frac {hb^{3}}{12}},\quad I_{xy}=I_{yx}=M_{xy}^{(2)}=0}$

On b és la base del rectangle i h la seva altura.

Tessel·lacions quadrades, perfectes i altres

Un rectangle perfecte d'ordre 9

Quadrat quadrat perfecte de menor ordre (1) i els tres quadrats quadrats perfectes més petites (2–4) – all are simple squared squares

Un rectangle tessel·lat per quadrats, rectangles o triangles rep el nom de rectangle "quadrat", "rectangulat", o "triangulat" (o "trianglat") respectivament. El rectangle tessel·lat és a més perfecte^[23][24] si les seves parts són semblants i finits en nombre i no hi ha dues parts d'igual mida. Si hi ha dos o més tessel·les són d'igual mida, la tessel·lació és imperfecta. En un rectangle triangulat perfecte (o imperfecte) els triangles han de ser triangles rectangles. Es pot trobar una base de dades de tots els rectangles, quadrats i altres formes perfectes coneguts a squaring.net.

El menor nombre de quadrats que calen per a tessel·lar perfectament un rectangle és 9^[25] i el menor nombre de quadrats que calen per "quadrar" perfectament un quadrat és 21, descobert computacionalment l'any 1978.^[26]

Un rectangle té costats commensurables si i només si és tessel·lable per un nombre finit de quadrats no iguals.^[23][27] Això mateix és veritat si les peces són triangles rectangles isòsceles diferents.

Les tessel·lacions de recangles amb altres formes que han rebut més interès són aquells fets amb poloòminos congruents no rectangulars, que permeten totes les rotacions i reflexions. També hi ha tessel·lacions amb poliàbolos congruents.

Vegeu també

• Paral·lelogram
• Quadrat
• Quadrilàter
• Polígon

Referències

1. Michel Helfgott. Geometría plana, Editorial Escuela Activa S. A.
2. «Archived copy». Arxivat de l'original el 2014-05-14. [Consulta: 20 juny 2013].
3. Definition of Oblong Arxivat 2017-07-07 a Wayback Machine.. Mathsisfun.com. Retrieved 2011-11-13.
4. Oblong – Geometry – Math Dictionary Arxivat 2009-04-08 a Wayback Machine.. Icoachmath.com. Retrieved 2011-11-13.
5. Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition", Information Age Publishing, 2008, pp. 34–36 ISBN 1-59311-695-0.
6. Owen Byer. Methods for Euclidean Geometry. MAA, 19 August 2010, p. 53–. ISBN 978-0-88385-763-2. Arxivat 2024-05-31 a Wayback Machine.
7. Gerard Venema, "Exploring Advanced Euclidean Geometry with GeoGebra", MAA, 2013, p. 56.
8. Josefsson Martin «Five Proofs of an Area Characterization of Rectangles». Forum Geometricorum, vol. 13, 2013, pàg. 17–21. Arxivat 2016-03-04 a Wayback Machine.
9. An Extended Classification of Quadrilaterals Arxivat 2019-12-30 a Wayback Machine. (En un extracte de De Villiers, M. 1996. Some Adventures in Euclidean Geometry. University of Durban-Westville.)
10. Sapiña, R. «Calculadora i demostració de l'àrea i perímetre d'un rectangle» (en castellà). Problemas y ecuaciones. Arxivat de l'original el 2020-06-26. ISSN: 2659-9899 [Consulta: 23 juny 2020].
11. Julio Rey Pastor et al. Geometría Analítica
12. Clemens: "Geometría. Con aplicaciones y solución de problemas"
13. Adaptació de la Introducción a la teoría de grupos de Alexándrov, Editorial URSS ISBN 9785354011292
14. Michel Helfgott. Op. cit.
15. G.M: Bruño. Elementos de Geometría
16. «Rectangle». Math Is Fun. Arxivat de l'original el 2023-12-07. [Consulta: 22 març 2024].
17. Tapson, Frank. «A Miscellany of Extracts from a Dictionary of Mathematics». Oxford University Press, July 1999. Arxivat de l'original el 2014-05-14. [Consulta: 20 juny 2013].
18. de Villiers, Michael, "Generalizing Van Aubel Using Duality", Mathematics Magazine 73 (4), Oct. 2000, pp. 303–307.
19. Cyclic Quadrilateral Incentre-Rectangle Arxivat 2011-09-28 a Wayback Machine. amb animació interactiva que mostra un com un rectangle es converteix en un 'rectangle creuat', suggerint que un 'rectangle creuat' es pot considerar un tipus de rectangle.
20. «An Unexpected Maximum in a Family of Rectangles». Mathematics Magazine, vol. 71, 4, 1998, pàg. 285–291. DOI: 10.1080/0025570X.1998.11996653. JSTOR: 2690700. Arxivat 2010-07-23 a Wayback Machine.
21. Lassak, M. «Approximation of convex bodies by rectangles». Geometriae Dedicata, vol. 47, 1993, pàg. 111–117. DOI: 10.1007/BF01263495.
22. Plantilla:Cite OEIS
23. R.L. Brooks «The dissection of rectangles into squares». Duke Math. J., vol. 7, 1, 1940, pàg. 312–340. DOI: 10.1215/S0012-7094-40-00718-9. Arxivat 2021-02-26 a Wayback Machine.
24. J.D. Skinner II «On the Dissection of Rectangles into Right-Angled Isosceles Triangles». Journal of Combinatorial Theory, Series B, vol. 80, 2, November 2000, pàg. 277–319. DOI: 10.1006/jctb.2000.1987.
25. Plantilla:Cite OEIS
26. «Squared Squares; Perfect Simples, Perfect Compounds and Imperfect Simples». www.squaring.net. Arxivat de l'original el 2021-10-23. [Consulta: 26 setembre 2021].
27. R. Sprague «Ũber die Zerlegung von Rechtecken in lauter verschiedene Quadrate» (en alemany). Journal für die reine und angewandte Mathematik, vol. 1940, 182, 1940, pàg. 60–64. DOI: 10.1515/crll.1940.182.60.