平面曲线上的亮点的切向量和法向量,以及标架在运动过程中的旋转。
平面曲线上的亮点的切向量和法向量,以及标架在运动过程中的旋转。
记r(t) 为欧式空间R3中的曲线,表示粒子在时间 t 时刻的位置向量。 弗勒内公式只适用于正则曲线,即速度向量r′(t)和加速度向量r′′(t)不为零的曲线。
记 s(t) 为 t时刻粒子所在位置到曲线上某定点的弧长:

由于假设r′ ≠ 0,因此可以将 t 表示为 s 的函数,因此可将曲线表示为弧长 s 的函数 r(s) = r(t(s))。 s 通常也被称为曲线的弧长参数。
对于由弧长参数定义的正则曲线 r(s),弗勒内标架 (或弗勒内基底)定义如下:



 螺旋线上弗勒内标架的运动。蓝色的箭头表示切向量,红色的箭头表示法向量,黑色的箭头表示副法向量。
螺旋线上弗勒内标架的运动。蓝色的箭头表示切向量,红色的箭头表示法向量,黑色的箭头表示副法向量。
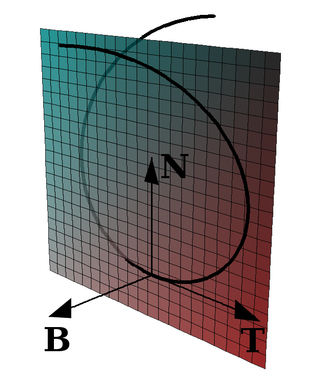
由于  所以 N 与 T 垂直。 方程 (3) 说明 B 垂直于 T 和 N,因此向量 T,N,B 互相垂直。
所以 N 与 T 垂直。 方程 (3) 说明 B 垂直于 T 和 N,因此向量 T,N,B 互相垂直。
弗勒内公式如下:

其中 κ 为曲线的曲率,τ 为曲线的挠率。
弗勒内公式有时也被称作弗勒内定理,并且可以写做矩阵的形式:[1]

其中的矩阵是反对称矩阵。
对弧长s求导,可以看成是对切方向的协变导数。