单位阶跃函数

單位階躍函數，又称赫维赛德阶跃函数，通常用 H 或 θ 表记，有时也会用 u、1 或 𝟙 表记，是一个由奥利弗·亥维赛提出的阶跃函数，参数为负时值为0，参数为正时值为1。

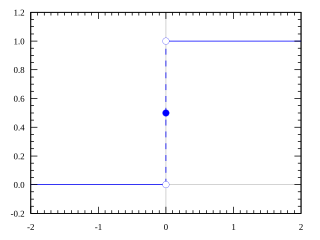
分段函数形式的定義如下：

${\displaystyle H[n]={\begin{cases}0,&n<0,\\1,&n\geq 0,\end{cases}}}$

另一种定义为：

${\displaystyle H(x)={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0\end{cases}}}$

或

${\displaystyle H(x)={\frac {1}{2}}\left(1+\operatorname {sgn}(x)\right)}$

它是個不連續函數，其微分是狄拉克δ函數。它是一個幾乎必然是零的隨機變數的累積分布函數。

事實上，${\displaystyle x=0}$的值在函數應用上並不重要，可以任意取。

連續函數逼近

• ${\displaystyle H(x)=\lim _{k\rightarrow \infty }{\frac {1}{2}}(1+\tanh kx)=\lim _{k\rightarrow \infty }{\frac {1}{1+\mathrm {e} ^{-2kx}}}}$

有許多可以以解析方式近似的函數^[1]，以下是二個例子：

• ${\displaystyle H(x)=\lim _{k\rightarrow \infty }{\frac {1}{2}}+{\frac {1}{\pi }}\arctan(kx)\ }$
• ${\displaystyle H(x)=\lim _{k\rightarrow \infty }{\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} (kx)\ }$

積分表示

${\displaystyle {\begin{aligned}H(x)&=\lim _{\varepsilon \to 0^{+}}-{\frac {1}{2\pi i}}\int _{-\infty }^{\infty }{\frac {1}{\tau +i\varepsilon }}e^{-ix\tau }d\tau \\&=\lim _{\varepsilon \to 0^{+}}{\frac {1}{2\pi i}}\int _{-\infty }^{\infty }{\frac {1}{\tau -i\varepsilon }}e^{ix\tau }d\tau .\end{aligned}}}$

参见

• 狄拉克δ函数
• 数学函数列表
• 拉普拉斯变换
• 负数
• 矩形函数
• 符号函数
• 阶梯响应