此條目介紹的是机器学习中的决策树。关于决策分析中的术语，请见「
决策树 」。
决策树学习 是统计学 、数据挖掘 和机器学习 中使用的一种预测建模方法。它使用决策树 作为预测模型
按预测结果的差异，决策树学习可细分两类。（1）分类树 ，其预测结果仅限于一组离散数值。树的每个分支对应一组由逻辑与 连接的分类特征，而该分支上的叶节点对应由上述特征可以预测出的分类标签。（2）回归树 ，其预测结果为连续值（例如实数 ）。
在决策分析中，一棵可视的决策树可以向使用者形象地展示决策 的结果和过程。在数据挖掘 和机器学习 中，一棵决策树主要用于描述数据（此后亦可基于习得的预测模型去支持决策 )。本页侧重描述数据挖掘 中的决策树。
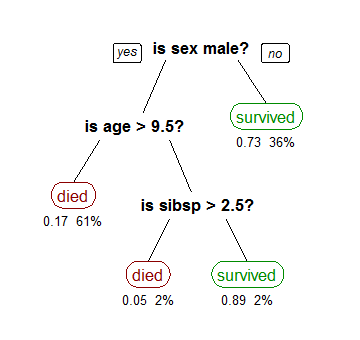
一个描述泰坦尼克号 上乘客生存的决策树 ("sibsp"指甲板上的兄妹和配偶)。每个决策叶下标识该类乘客的生存几率和观察到的比率 在数据挖掘中决策树训练是一个常用的方法。目标是创建一个模型来预测样本的目标值。例如右图。每个内部节点对应于一个输入属性，子节点代表父节点的属性的可能取值。每个叶子节点代表输入属性得到的可能输出值。
一棵树的训练过程为：根据一个指标，分裂训练集为几个子集。这个过程不断的在产生的子集里重复递归进行，即递归分割。当一个训练子集的类标都相同时递归 停止。这种决策树的自顶向下归纳 (TDITD) [ 1] 贪心算法 的一种, 也是目前为止最为常用的一种训练方法，但不是唯一的方法。
(
x
,
Y
)
=
(
x
1
,
x
2
,
x
3
,
.
.
.
,
x
k
,
Y
)
{\displaystyle ({\textbf {x}},Y)=(x_{1},x_{2},x_{3},...,x_{k},Y)}
其中Y是目标值，向量x 由这些属性构成, x1 , x2 , x3 等等，用来得到目标值。
在数据挖掘中，决策树主要有两种类型:
分类树 的输出是样本的类标（例如花的分類，股票漲跌等）。回归树 的输出是一个实数 (例如房子的价格，病人待在医院的时间等)。术语分类和回归树 (CART) 包含了上述两种决策树, 最先由Breiman 等提出.[ 2] [ 2]
有些集成 的方法产生多棵树：
装袋算法（Bagging） , 是一个早期的集成方法，用有放回抽样法来训练多棵决策树，最终结果用投票法产生。[ 3] 随机森林（Random Forest） 提升树（Boosting Tree） [ 4] [ 5] 旋转森林（Rotation forest） – 每棵树的训练首先使用主元分析法 (PCA)。[ 6] 还有其他很多决策树算法，常见的有:
ID3算法 C4.5算法 CHi-squared Automatic Interaction Detector (CHAID ) . 在生成树的过程中用多层分裂.[ 7] MARS :可以更好的处理数值型数据。
构建决策树时通常采用自上而下的方法，在每一步选择一个最好的属性来分裂。[ 8]
ID3 , C4.5 和 C5.0 决策树的生成使用信息增益 。信息增益 是基于信息论 中信息熵 与資訊本體 理论.
信息熵 定义为：
H
(
T
)
=
I
E
(
p
1
,
p
2
,
.
.
.
,
p
J
)
=
−
∑
i
=
1
J
p
i
log
2
p
i
{\displaystyle \mathrm {H} (T)=\operatorname {I} _{E}\left(p_{1},p_{2},...,p_{J}\right)=-\sum _{i=1}^{J}{p_{i}\log _{2}p_{i}}}
其中
p
1
,
p
2
,
.
.
.
{\displaystyle p_{1},p_{2},...}
[ 9]
I
G
(
T
,
a
)
⏞
Information Gain
=
H
(
T
)
⏞
Entropy (parent)
−
H
(
T
|
a
)
⏞
Weighted Sum of Entropy (Children)
{\displaystyle \overbrace {IG(T,a)} ^{\text{Information Gain}}=\overbrace {\mathrm {H} (T)} ^{\text{Entropy (parent)}}-\overbrace {\mathrm {H} (T|a)} ^{\text{Weighted Sum of Entropy (Children)}}}
=
−
∑
i
=
1
J
p
i
log
2
p
i
−
∑
a
p
(
a
)
∑
i
=
1
J
−
Pr
(
i
|
a
)
log
2
Pr
(
i
|
a
)
{\displaystyle =-\sum _{i=1}^{J}p_{i}\log _{2}{p_{i}}-\sum _{a}{p(a)\sum _{i=1}^{J}-\Pr(i|a)\log _{2}{\Pr(i|a)}}}
例如，数据集有4个属性：outlook (sunny, overcast, rainy), temperature (hot, mild, cool), humidity (high, normal), and windy (true, false), 目标值play （yes, no）, 总共14个数据点。为建造决策树，需要比较4棵决策树的信息增益，每棵决策树用一种属性做划分。信息增益最高的划分作为第一次划分，并在每个子节点继续此过程，直至其信息增益为0。
使用属性windy 做划分时，产生2个子节点：windy 值为真与为假。当前数据集，6个数据点的windy 值为真，其中3个点的play 值为真，3个点的play 值为假；其余8个数据点的windy 为假，其中6个点的play 值为真，2个点的play 值为假。 windy =true的子节点的信息熵计算为：
I
E
(
[
3
,
3
]
)
=
−
3
6
log
2
3
6
−
3
6
log
2
3
6
=
−
1
2
log
2
1
2
−
1
2
log
2
1
2
=
1
{\displaystyle I_{E}([3,3])=-{\frac {3}{6}}\log _{2}^{}{\frac {3}{6}}-{\frac {3}{6}}\log _{2}^{}{\frac {3}{6}}=-{\frac {1}{2}}\log _{2}^{}{\frac {1}{2}}-{\frac {1}{2}}\log _{2}^{}{\frac {1}{2}}=1}
windy =false的子节点的信息熵计算为：
I
E
(
[
6
,
2
]
)
=
−
6
8
log
2
6
8
−
2
8
log
2
2
8
=
−
3
4
log
2
3
4
−
1
4
log
2
1
4
=
0.8112781
{\displaystyle I_{E}([6,2])=-{\frac {6}{8}}\log _{2}^{}{\frac {6}{8}}-{\frac {2}{8}}\log _{2}^{}{\frac {2}{8}}=-{\frac {3}{4}}\log _{2}^{}{\frac {3}{4}}-{\frac {1}{4}}\log _{2}^{}{\frac {1}{4}}=0.8112781}
这个划分（使用属性windy ）的信息熵是两个子节点信息熵的加权和：
I
E
(
[
3
,
3
]
,
[
6
,
2
]
)
=
I
E
(
windy or not
)
=
6
14
⋅
1
+
8
14
⋅
0.8112781
=
0.8921589
{\displaystyle I_{E}([3,3],[6,2])=I_{E}({\text{windy or not}})={\frac {6}{14}}\cdot 1+{\frac {8}{14}}\cdot 0.8112781=0.8921589}
为计算使用属性windy 的信息增益，必须先计算出最初（未划分）的数据集的信息熵，数据集的play 有9个yes与5个no：
I
E
(
[
9
,
5
]
)
=
−
9
14
log
2
9
14
−
5
14
log
2
5
14
=
0.940286
{\displaystyle I_{E}([9,5])=-{\frac {9}{14}}\log _{2}^{}{\frac {9}{14}}-{\frac {5}{14}}\log _{2}{\frac {5}{14}}=0.940286}
使用属性windy 的信息增益是：
I
G
(
windy
)
=
I
E
(
[
9
,
5
]
)
−
I
E
(
[
3
,
3
]
,
[
6
,
2
]
)
=
0.940286
−
0.8921589
=
0.0481271
{\displaystyle IG({\text{windy}})=I_{E}([9,5])-I_{E}([3,3],[6,2])=0.940286-0.8921589=0.0481271}
与其他的数据挖掘算法相比，决策树有许多优点:
易于理解和解释 人们很容易理解决策树的意义。只需很少的数据准备 其他技术往往需要数据归一化。即可以处理数值型数据也可以处理類別變數 数据 。其他技术往往只能处理一种数据类型。例如关联规则只能处理类别型的而神经网络只能处理数值型的数据。使用白箱 输出结果容易通过模型的结构来解释。而神经网络是黑箱模型，很难解释输出的结果。可以通过测试集来验证模型的性能 。可以考虑模型的稳定性。強健控制 可以很好的处理大规模数据 。
训练一棵最优的决策树是一个完全NP问题。[ 10] [ 11] 贪心算法 来达到局部最优。这样的算法没办法得到最优的决策树。
决策树创建的过度复杂会导致无法很好的预测训练集之外的数据。这称作过拟合 .[ 12] 剪枝 机制可以避免这种问题。
有些问题决策树没办法很好的解决,例如 异或 问题。解决这种问题的时候，决策树会变得过大。 要解决这种问题，只能改变问题的领域[ 13] 統計關係學習 歸納邏輯程式設計
在决策树中, 从根节点到叶节点的路径采用汇合。
而在决策图中, 可以采用{{ts1|en|Minimum description length|最小描述長度]] (MML)来汇合两条或多条路径。[ 15]
演化算法可以用来避免局部最优的问题[ 16] [ 17]
Quinlan, J. R., (1986). Induction of Decision Trees. Machine Learning 1: 81-106, Kluwer Academic Publishers
Breiman, Leo; Friedman, J. H., Olshen, R. A., & Stone, C. J. Classification and regression trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software. 1984. ISBN 978-0-412-04841-8 Breiman, L. (1996). Bagging Predictors. "Machine Learning, 24": pp. 123-140.
Friedman, J. H. (1999). Stochastic gradient boosting. Stanford University.
Hastie, T., Tibshirani, R., Friedman, J. H. (2001). The elements of statistical learning : Data mining, inference, and prediction. New York: Springer Verlag.
Rodriguez, J.J. and Kuncheva, L.I. and Alonso, C.J. (2006), Rotation forest: A new classifier ensemble method, IEEE Transactions on Pattern Analysis and Machine Intelligence, 28(10):1619-1630.
Kass, G. V. An exploratory technique for investigating large quantities of categorical data. Applied Statistics. 1980, 29 (2): 119–127. JSTOR 2986296 doi:10.2307/2986296 Rokach, L.; Maimon, O. Top-down induction of decision trees classifiers-a survey. IEEE Transactions on Systems, Man, and Cybernetics, Part C. 2005, 35 (4): 476–487. doi:10.1109/TSMCC.2004.843247 Hyafil, Laurent; Rivest, RL. Constructing Optimal Binary Decision Trees is NP-complete. Information Processing Letters. 1976, 5 (1): 15–17. doi:10.1016/0020-0190(76)90095-8 Murthy S. (1998). Automatic construction of decision trees from data: A multidisciplinary survey. Data Mining and Knowledge Discovery
存档副本 . [2012-05-26 ] . （原始内容存档 于2008-03-21）.Papagelis A., Kalles D.(2001). Breeding Decision Trees Using Evolutionary Techniques, Proceedings of the Eighteenth International Conference on Machine Learning, p.393-400, June 28-July 01, 2001
Barros, Rodrigo C., Basgalupp, M. P., Carvalho, A. C. P. L. F., Freitas, Alex A. (2011). A Survey of Evolutionary Algorithms for Decision-Tree Induction . IEEE Transactions on Systems, Man and Cybernetics, Part C: Applications and Reviews, vol. 42, n. 3, p. 291-312, May 2012. 
![{\displaystyle I_{E}([3,3])=-{\frac {3}{6}}\log _{2}^{}{\frac {3}{6}}-{\frac {3}{6}}\log _{2}^{}{\frac {3}{6}}=-{\frac {1}{2}}\log _{2}^{}{\frac {1}{2}}-{\frac {1}{2}}\log _{2}^{}{\frac {1}{2}}=1}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cf74d50ef790bf5ecdcef0914265086a2a7be9dc)
![{\displaystyle I_{E}([6,2])=-{\frac {6}{8}}\log _{2}^{}{\frac {6}{8}}-{\frac {2}{8}}\log _{2}^{}{\frac {2}{8}}=-{\frac {3}{4}}\log _{2}^{}{\frac {3}{4}}-{\frac {1}{4}}\log _{2}^{}{\frac {1}{4}}=0.8112781}](http://wikimedia.org/api/rest_v1/media/math/render/svg/73ef3f50981ec9b21ef906aa433e815ea74c4abc)
![{\displaystyle I_{E}([3,3],[6,2])=I_{E}({\text{windy or not}})={\frac {6}{14}}\cdot 1+{\frac {8}{14}}\cdot 0.8112781=0.8921589}](http://wikimedia.org/api/rest_v1/media/math/render/svg/139b37ab183e44a82ab8be436d9cf213b461827a)
![{\displaystyle I_{E}([9,5])=-{\frac {9}{14}}\log _{2}^{}{\frac {9}{14}}-{\frac {5}{14}}\log _{2}{\frac {5}{14}}=0.940286}](http://wikimedia.org/api/rest_v1/media/math/render/svg/93ca10deb737dae236e75e9c276dd0f4a449a80f)
![{\displaystyle IG({\text{windy}})=I_{E}([9,5])-I_{E}([3,3],[6,2])=0.940286-0.8921589=0.0481271}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a734109aca06807d1dc0f5e2be2486b36c7140c3)
