中点法

数值分析裡的中点法（midpoint method）是求解常微分方程的一種数值方法，屬於單步法。

${\displaystyle y'(t)=f(t,y(t)),\quad y(t_{0})=y_{0}.}$

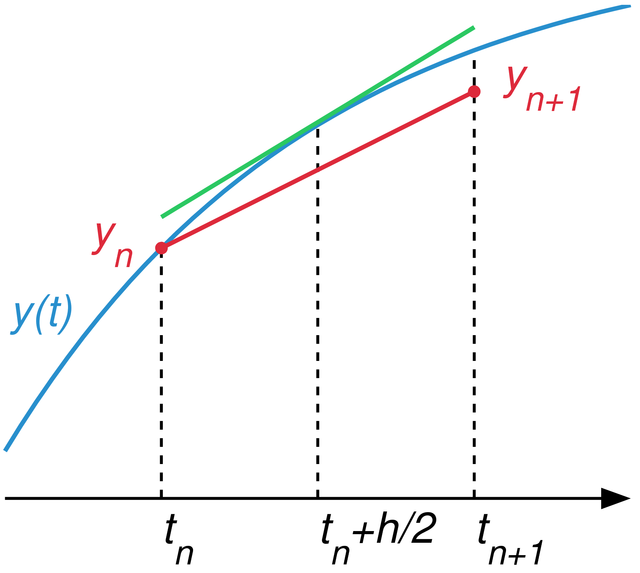中點法的圖示說明，假設${\displaystyle y_{n}}$等於${\displaystyle y(t_{n})}$的實際值。中點法計算${\displaystyle y_{n+1}}$讓紅色的弦近似平行於中點處的切線（綠色）

上式的顯式中點法為

${\displaystyle y_{n+1}=y_{n}+hf\left(t_{n}+{\frac {h}{2}},y_{n}+{\frac {h}{2}}f(t_{n},y_{n})\right),}$

1e

隱式中點法為

${\displaystyle y_{n+1}=y_{n}+hf\left(t_{n}+{\frac {h}{2}},{\frac {1}{2}}(y_{n}+y_{n+1})\right),}$

1i

${\displaystyle n=0,1,2,\dots }$。此處${\displaystyle h}$是步階長度，是一個小的正數，${\displaystyle t_{n}=t_{0}+nh,}$，而${\displaystyle y_{n}}$是計算${\displaystyle y(t_{n})}$的近似值。顯式中點法也稱為是改良的歐拉方法（modified Euler method）^[1]，隱式中點式是最簡單的配置法（英语：collocation method）（Collocation method），可用在哈密頓力學，也就是辛積分器（英语：symplectic integrator）。

此方法的名稱是因為上述公式會用到函數在${\displaystyle t=t_{n}+h/2={\tfrac {t_{n}+t_{n+1}}{2}}}$位置的值，也就是在${\displaystyle t_{n}}$以及${\displaystyle t_{n+1}}$中點時的值，前者的值已知，後者的值未知，在計算中點的值時，也需要有一些假設，才能進行計算。

配合圖示（見右圖）會比較容易理解此一方法。在原始的欧拉方法裡，會用${\displaystyle f(t_{n},y_{n})}$，計算曲線在${\displaystyle (t_{n},y_{n})}$處的切線。此切線和垂直線${\displaystyle t=t_{n+1}}$的交點即為下一個點${\displaystyle y_{n+1}}$的值。不過，若此函數的二階導數在時間${\displaystyle t_{n}}$和${\displaystyle t_{n+1}}$的區間均為正, 或是均為負（如圖中的例子），隨著${\displaystyle h}$加大，曲線和切線的距離會越來越遠，導致大誤差。圖中所畫的中點的切線（上方，綠線）比較可以近似這段曲線。不過因為要求解的就是此一曲線，時間${\displaystyle t_{n}}$的資訊已知，其他資訊不足，可能無法精準的畫出中點處的切線。

因此，會先用原始的歐拉方法估計在中點的${\displaystyle y(t)}$值，再用${\displaystyle f()}$以及估計的中點資訊，計算切線斜率。用改善後的切線從${\displaystyle y_{n}}$計算${\displaystyle y_{n+1}}$的值。最後一步即為圖的紅色弦線。因為紅色弦線是估計值，用的是${\displaystyle y(t)}$在中點處的估計值，不一定真的會和綠線（真正的中點切線）平行，仍會有誤差。

中點法每一步的局部誤差是${\displaystyle O\left(h^{3}\right)}$，全域誤差是${\displaystyle O\left(h^{2}\right)}$。其運算比歐拉方法要大，但在${\displaystyle h\to 0}$的過程中，中點法的誤差會比歐拉方法降低的更快。

此法也是高階方法（如龙格-库塔法）的範例之一。

中點法的推導

微分方程${\displaystyle y'=y,\ y(0)=1}$的数值积分求解图。

  蓝：欧拉法

  绿：中点法

  红：精确解：${\displaystyle y=e^{t}}$

步长${\displaystyle h=1.0}$。

同一個方程的數值方法求解，步长縮減為${\displaystyle h=0.25.}$，可以看出中點法的收斂比歐拉法要快

中點法可以視為是改良版的欧拉方法

${\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}),\,}$

因此用類似的方式推導。 推導欧拉法的關鍵是以下的近似等式

${\displaystyle y(t+h)\approx y(t)+hf(t,y(t))}$

2

是源自以下的斜率公式

${\displaystyle y'(t)\approx {\frac {y(t+h)-y(t)}{h}}}$

3

，其中${\displaystyle y'=f(t,y).}$

在中點法中，將(3)改為更準確的式子

${\displaystyle y'\left(t+{\frac {h}{2}}\right)\approx {\frac {y(t+h)-y(t)}{h}}}$

因此可以得到以下類似(3)式，計算${\displaystyle y(t+h)}$的式子

${\displaystyle y(t+h)\approx y(t)+hf\left(t+{\frac {h}{2}},y\left(t+{\frac {h}{2}}\right)\right).}$

4

在上式中，因為還不知道${\displaystyle y}$在${\displaystyle t+h/2}$的值，無法用上式直接計算${\displaystyle y(t+h)}$。解法是用欧拉方法來求解${\displaystyle y(t+h/2)}$:

${\displaystyle y\left(t+{\frac {h}{2}}\right)\approx y(t)+{\frac {h}{2}}y'(t)=y(t)+{\frac {h}{2}}f(t,y(t)),}$

代入(4)式中，可得

${\displaystyle y(t+h)\approx y(t)+hf\left(t+{\frac {h}{2}},y(t)+{\frac {h}{2}}f(t,y(t))\right)}$

以上則是顯式的中點法(1e)。

隱式中點法(1i)可以將此時間內的波形假設為直線，中間步數${\displaystyle t+h/2}$的值用${\displaystyle y(t)}$和${\displaystyle y(t+h)}$的平均值來表示

${\displaystyle y\left(t+{\frac {h}{2}}\right)\approx {\frac {1}{2}}{\bigl (}y(t)+y(t+h){\bigr )}}$

因此

${\displaystyle {\frac {y(t+h)-y(t)}{h}}\approx y'\left(t+{\frac {h}{2}}\right)\approx k=f\left(t+{\frac {h}{2}},{\frac {1}{2}}{\bigl (}y(t)+y(t+h){\bigr )}\right)}$

因為隱式方法的時間對稱性，局部誤差中${\displaystyle h}$的偶次項都消去了，局部誤差的階數是＼${\displaystyle {\mathcal {O}}(h^{3})}$。

相關條目

• 黎曼和
• Heun方法
• 蛙跳积分法和韦尔莱积分法