彎曲 （bending ）也稱為屈曲 （flexure ），為材料力學 的名詞．是指一形狀狹長的結構件固體，受到和其長軸垂直的外力時，固體變形的情形。
工字梁 的彎曲若結構件在某一方向長度很長，另外二方向的尺寸是該方向尺寸的1/10或更小，即滿足上述形狀狹長的定義[ 1] 梁 。例如衣櫉中的橫桿會因為衣架 上衣服的總重量而變形，就是梁受力彎曲的例子。另外方面，殼層
若沒有具體說明物體的形狀，「彎曲」可以指任何外形物體的彎曲。在工程應用上，有時會說明彎曲物體的形狀，例如「桿的彎曲」（bending of rods）[ 2] [ 1] 平板彎曲 [ 3] [ 2]
水平梁受力彎曲，梁上半部（B）受到壓應力，梁下半部（A）受到拉伸應力 梁在受到側向力時，其內部會變形，而且會產生應力 。準靜（quasi-static）彎曲是假設彎曲產生的形變 以及應力不隨時間而變化。若考慮一水平梁，兩側固定，中間受到往下的力，梁的上半部會受到壓縮力，而梁的下半部會受到拉伸力。由於其側向力，會產生以下兩種內應力：
和側向力平行的剪應力 ，以及和受力方向垂直的互補剪應力
梁上半部受到的直接壓應力 ，以及梁下半部受到的直接拉伸應力。 後二個力會形成力偶 或是矩 彎矩 [ 1]
方程式
σ
=
M
y
I
x
{\displaystyle \sigma ={\tfrac {My}{I_{x}}}}
极限状态 。
上述推導只用在截面對稱的條件。針對非對稱截面的均質梁，梁的最大彎曲應力如下：
σ
x
(
y
,
z
)
=
M
z
I
y
−
M
y
I
y
z
I
y
I
z
−
I
y
z
2
y
+
M
y
I
z
−
M
z
I
y
z
I
y
I
z
−
I
y
z
2
z
{\displaystyle \sigma _{x}(y,z)={\frac {M_{z}~I_{y}-M_{y}~I_{yz}}{I_{y}~I_{z}-I_{yz}^{2}}}y+{\frac {M_{y}~I_{z}-M_{z}~I_{yz}}{I_{y}~I_{z}-I_{yz}^{2}}}z}
[ 6] 其中
y
,
z
{\displaystyle y,z}
M
y
{\displaystyle M_{y}}
M
z
{\displaystyle M_{z}}
幾何中心 y軸和z軸的彎軸。
I
y
{\displaystyle I_{y}}
I
z
{\displaystyle I_{z}}
截面二次軸矩 ，
I
y
z
{\displaystyle I_{yz}}
M
y
,
M
z
,
I
y
,
I
z
,
I
y
z
{\displaystyle M_{y},M_{z},I_{y},I_{z},I_{yz}}
梁的動態彎曲（dynamic bending）[ 8] 丹尼尔·伯努利 在18世紀中所提出的。伯努利的振動梁運動方程容易高估梁的自然頻率 ，約翰·斯特拉特，第三代瑞利男爵 在1877年多加入了中間平面的旋轉項，有些微改善。1921年斯蒂芬·铁摩辛柯 在彎曲梁的動態響應中多考慮了剪力的影響，大幅提昇準確度。因此此定理可以用在有高頻振動，不適用動態丹尼尔·伯努利方程場合。歐拉-伯努力以及铁摩辛柯的彎曲梁動態方程仍廣泛在工程界使用。
若梁沒有側向力時，其振動方程如下
E
I
∂
4
w
∂
x
4
+
m
∂
2
w
∂
t
2
=
0
{\displaystyle EI~{\cfrac {\partial ^{4}w}{\partial x^{4}}}+m~{\cfrac {\partial ^{2}w}{\partial t^{2}}}=0}
梁不受力下的簡諧振動可以表示如下
w
(
x
,
t
)
=
Re
[
w
^
(
x
)
e
−
i
ω
t
]
⟹
∂
2
w
∂
t
2
=
−
ω
2
w
(
x
,
t
)
{\displaystyle w(x,t)={\text{Re}}[{\hat {w}}(x)~e^{-i\omega t}]\quad \implies \quad {\cfrac {\partial ^{2}w}{\partial t^{2}}}=-\omega ^{2}~w(x,t)}
其彎曲方程為
E
I
d
4
w
^
d
x
4
−
m
ω
2
w
^
=
0
{\displaystyle EI~{\cfrac {\mathrm {d} ^{4}{\hat {w}}}{\mathrm {d} x^{4}}}-m\omega ^{2}{\hat {w}}=0}
上式的通解為
w
^
=
A
1
cosh
(
β
x
)
+
A
2
sinh
(
β
x
)
+
A
3
cos
(
β
x
)
+
A
4
sin
(
β
x
)
{\displaystyle {\hat {w}}=A_{1}\cosh(\beta x)+A_{2}\sinh(\beta x)+A_{3}\cos(\beta x)+A_{4}\sin(\beta x)}
其中
A
1
,
A
2
,
A
3
,
A
4
{\displaystyle A_{1},A_{2},A_{3},A_{4}}
β
:=
(
m
E
I
ω
2
)
1
/
4
{\displaystyle \beta :=\left({\cfrac {m}{EI}}~\omega ^{2}\right)^{1/4}}
若梁沒有側向力時，鐵木辛柯﹣瑞利理論的簡諧振動方程如下
E
I
d
4
w
^
d
x
4
+
m
ω
2
(
J
m
+
E
I
k
A
G
)
d
2
w
^
d
x
2
+
m
ω
2
(
ω
2
J
k
A
G
−
1
)
w
^
=
0
{\displaystyle EI~{\cfrac {\mathrm {d} ^{4}{\hat {w}}}{\mathrm {d} x^{4}}}+m\omega ^{2}\left({\cfrac {J}{m}}+{\cfrac {EI}{kAG}}\right){\cfrac {\mathrm {d} ^{2}{\hat {w}}}{\mathrm {d} x^{2}}}+m\omega ^{2}\left({\cfrac {\omega ^{2}J}{kAG}}-1\right)~{\hat {w}}=0}
此式求解時，考慮
w
{\displaystyle w}
e
k
x
{\displaystyle e^{kx}}
特徵方程式
α
k
4
+
β
k
2
+
γ
=
0
;
α
:=
E
I
,
β
:=
m
ω
2
(
J
m
+
E
I
k
A
G
)
,
γ
:=
m
ω
2
(
ω
2
J
k
A
G
−
1
)
{\displaystyle \alpha ~k^{4}+\beta ~k^{2}+\gamma =0~;~~\alpha :=EI~,~~\beta :=m\omega ^{2}\left({\cfrac {J}{m}}+{\cfrac {EI}{kAG}}\right)~,~~\gamma :=m\omega ^{2}\left({\cfrac {\omega ^{2}J}{kAG}}-1\right)}
此四次方程 的解為
k
1
=
+
z
+
,
k
2
=
−
z
+
,
k
3
=
+
z
−
,
k
4
=
−
z
−
{\displaystyle k_{1}=+{\sqrt {z_{+}}}~,~~k_{2}=-{\sqrt {z_{+}}}~,~~k_{3}=+{\sqrt {z_{-}}}~,~~k_{4}=-{\sqrt {z_{-}}}}
其中
z
+
:=
−
β
+
β
2
−
4
α
γ
2
α
,
z
−
:=
−
β
−
β
2
−
4
α
γ
2
α
{\displaystyle z_{+}:={\cfrac {-\beta +{\sqrt {\beta ^{2}-4\alpha \gamma }}}{2\alpha }}~,~~z_{-}:={\cfrac {-\beta -{\sqrt {\beta ^{2}-4\alpha \gamma }}}{2\alpha }}}
無外力振動下，鐵木辛柯﹣瑞利梁方程的通解為
w
^
=
A
1
e
k
1
x
+
A
2
e
−
k
1
x
+
A
3
e
k
3
x
+
A
4
e
−
k
3
x
{\displaystyle {\hat {w}}=A_{1}~e^{k_{1}x}+A_{2}~e^{-k_{1}x}+A_{3}~e^{k_{3}x}+A_{4}~e^{-k_{3}x}}
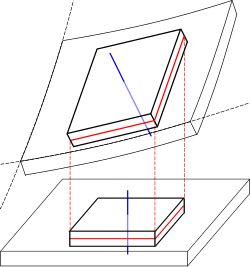
薄板的變形，其中突顯其位移、中表面（紅色）以及中表面的法向（藍色） 梁的特點是其中一個方向的尺寸遠大於另外二個方向的尺寸。一結構若其中一個方向的尺寸遠小於另外二個方向的尺寸，則稱為平板。有許多理論要描述平板在受力下的形變以及應力分佈（板理论 ），其中有二種理論比較常用，分別是
克希荷夫–勒夫平板理論（Kirchhoff–Love theory of plates，也稱為經典平板理論）
明德林–賴斯納平板理論（Mindlin–Reissner plate theory，也稱為一階平板理論）
克希荷夫–勒夫平板理論
和中表面垂直的直線在形變後仍然是直線
和中表面垂直的直線在形變後仍然和中表面直線垂直
在形變前後，平板的厚度不會變化。 上述的假設意味著
u
α
(
x
)
=
−
x
3
∂
w
0
∂
x
α
=
−
x
3
w
,
α
0
;
α
=
1
,
2
u
3
(
x
)
=
w
0
(
x
1
,
x
2
)
{\displaystyle {\begin{aligned}u_{\alpha }(\mathbf {x} )&=-x_{3}~{\frac {\partial w^{0}}{\partial x_{\alpha }}}=-x_{3}~w_{,\alpha }^{0}~;~~\alpha =1,2\\u_{3}(\mathbf {x} )&=w^{0}(x_{1},x_{2})\end{aligned}}}
其中
u
{\displaystyle \mathbf {u} }
w
0
{\displaystyle w^{0}}
應變和位移的關係如下
ε
α
β
=
−
x
3
w
,
α
β
0
ε
α
3
=
0
ε
33
=
0
{\displaystyle {\begin{aligned}\varepsilon _{\alpha \beta }&=-x_{3}~w_{,\alpha \beta }^{0}\\\varepsilon _{\alpha 3}&=0\\\varepsilon _{33}&=0\end{aligned}}}
平衡方程式為
M
α
β
,
α
β
+
q
(
x
)
=
0
;
M
α
β
:=
∫
−
h
h
x
3
σ
α
β
d
x
3
{\displaystyle M_{\alpha \beta ,\alpha \beta }+q(x)=0~;~~M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}}
其中
q
(
x
)
{\displaystyle q(x)}
若以位移來表示，在沒有外力下，各向同性、線彈性平板的平衡方程為
w
,
1111
0
+
2
w
,
1212
0
+
w
,
2222
0
=
0
{\displaystyle w_{,1111}^{0}+2~w_{,1212}^{0}+w_{,2222}^{0}=0}
若以直接張量表示法，可以表示如下
∇
2
∇
2
w
=
0
{\displaystyle \nabla ^{2}\nabla ^{2}w=0}
明德林–賴斯納平板理論
u
α
(
x
)
=
−
x
3
φ
α
;
α
=
1
,
2
u
3
(
x
)
=
w
0
(
x
1
,
x
2
)
{\displaystyle {\begin{aligned}u_{\alpha }(\mathbf {x} )&=-x_{3}~\varphi _{\alpha }~;~~\alpha =1,2\\u_{3}(\mathbf {x} )&=w^{0}(x_{1},x_{2})\end{aligned}}}
其中
φ
α
{\displaystyle \varphi _{\alpha }}
依照以上假設，應變和位移之間的關係是
ε
α
β
=
−
x
3
φ
α
,
β
ε
α
3
=
1
2
κ
(
w
,
α
0
−
φ
α
)
ε
33
=
0
{\displaystyle {\begin{aligned}\varepsilon _{\alpha \beta }&=-x_{3}~\varphi _{\alpha ,\beta }\\\varepsilon _{\alpha 3}&={\cfrac {1}{2}}~\kappa \left(w_{,\alpha }^{0}-\varphi _{\alpha }\right)\\\varepsilon _{33}&=0\end{aligned}}}
其中
κ
{\displaystyle \kappa }
平衡方程為
M
α
β
,
β
−
Q
α
=
0
Q
α
,
α
+
q
=
0
{\displaystyle {\begin{aligned}&M_{\alpha \beta ,\beta }-Q_{\alpha }=0\\&Q_{\alpha ,\alpha }+q=0\end{aligned}}}
其中
Q
α
:=
κ
∫
−
h
h
σ
α
3
d
x
3
{\displaystyle Q_{\alpha }:=\kappa ~\int _{-h}^{h}\sigma _{\alpha 3}~dx_{3}}
平板的動態理論會決定在平板上震波的傳播，以及其駐波以及振動模態。克希荷夫平板動態彎曲的統御方程如下
M
α
β
,
α
β
−
q
(
x
,
t
)
=
J
1
w
¨
0
−
J
3
w
¨
,
α
α
0
{\displaystyle M_{\alpha \beta ,\alpha \beta }-q(x,t)=J_{1}~{\ddot {w}}^{0}-J_{3}~{\ddot {w}}_{,\alpha \alpha }^{0}}
其中（假設板的密度為
ρ
=
ρ
(
x
)
{\displaystyle \rho =\rho (x)}
J
1
:=
∫
−
h
h
ρ
d
x
3
;
J
3
:=
∫
−
h
h
x
3
2
ρ
d
x
3
{\displaystyle J_{1}:=\int _{-h}^{h}\rho ~dx_{3}~;~~J_{3}:=\int _{-h}^{h}x_{3}^{2}~\rho ~dx_{3}}
以及
w
¨
0
=
∂
2
w
0
∂
t
2
;
w
¨
,
α
β
0
=
∂
2
w
¨
0
∂
x
α
∂
x
β
{\displaystyle {\ddot {w}}^{0}={\frac {\partial ^{2}w^{0}}{\partial t^{2}}}~;~~{\ddot {w}}_{,\alpha \beta }^{0}={\frac {\partial ^{2}{\ddot {w}}^{0}}{\partial x_{\alpha }\,\partial x_{\beta }}}}
以下是一些圓形平板的振動模態。
mode k = 0, p = 1
mode k = 0, p = 2
mode k = 1, p = 2
Boresi, A. P. and Schmidt, R. J. and Sidebottom, O. M., 1993, Advanced mechanics of materials , John Wiley and Sons, New York.
Libai, A. and Simmonds, J. G., 1998, The nonlinear theory of elastic shells , Cambridge University Press.
Timoshenko, S. and Woinowsky-Krieger, S., 1959, Theory of plates and shells , McGraw-Hill.
Shigley J, "Mechanical Engineering Design", p44, International Edition, pub McGraw Hill, 1986, ISBN 0-07-100292-8 Gere, J. M. and Timoshenko, S.P., 1997, Mechanics of Materials , PWS Publishing Company.
Cook and Young, 1995, Advanced Mechanics of Materials, Macmillan Publishing Company: New York
Thomson, W. T., 1981, Theory of Vibration with Applications
Han, S. M, Benaroya, H. and Wei, T., 1999, "Dynamics of transversely vibrating beams using four engineering theories," Journal of Sound and Vibration , vol. 226, no. 5, pp. 935–988.
Rosinger, H. E. and Ritchie, I. G., 1977, On Timoshenko's correction for shear in vibrating isotropic beams, J. Phys. D: Appl. Phys., vol. 10, pp. 1461–1466.
![{\displaystyle w(x,t)={\text{Re}}[{\hat {w}}(x)~e^{-i\omega t}]\quad \implies \quad {\cfrac {\partial ^{2}w}{\partial t^{2}}}=-\omega ^{2}~w(x,t)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7b17ad3e37e2553884da6fcb9dffd7487039774e)
![{\displaystyle {\begin{aligned}&EI~{\frac {\partial ^{4}w}{\partial x^{4}}}+m~{\frac {\partial ^{2}w}{\partial t^{2}}}-\left(J+{\frac {EIm}{kAG}}\right){\frac {\partial ^{4}w}{\partial x^{2}~\partial t^{2}}}+{\frac {Jm}{kAG}}~{\frac {\partial ^{4}w}{\partial t^{4}}}\\[6pt]={}&q(x,t)+{\frac {J}{kAG}}~{\frac {\partial ^{2}q}{\partial t^{2}}}-{\frac {EI}{kAG}}~{\frac {\partial ^{2}q}{\partial x^{2}}}\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5b65d649cab51d29f4b0bb8e69a8bbccb9364b44)
![{\displaystyle {\begin{aligned}k&={\frac {5+5\nu }{6+5\nu }}\quad {\text{rectangular cross-section}}\\[6pt]&={\frac {6+12\nu +6\nu ^{2}}{7+12\nu +4\nu ^{2}}}\quad {\text{circular cross-section}}\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a8c11a187caa54d9696a9077b73e9bcd49ea0962)
