五角錐球狀屋頂

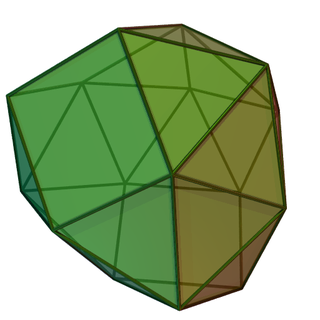
五角錐球狀屋頂（日語：五角錐球形屋根^[1]、英語：Disphenocingulum）是一種由20個三角形和4個正方形組成的二十四面體^[2]，為詹森多面體的其中一個，索引為J₉₀^[3]。其可以藉由合併2個去除2個三角形面的球狀屋頂來構造，但它無法由柏拉圖立體（正多面體）和阿基米得立體（半正多面體）經過切割、增補而得來，是詹森多面體中的基本立體之一。詹森多面體是凸多面體，面皆由正多邊形組成但不屬於均勻多面體，共有92種。這些立體最早在1966年由諾曼·詹森（英语：Norman Johnson (mathematician)）（Norman Johnson）命名並給予描述^[4]。

五角錐球狀屋頂

類別	詹森多面體 J89 - J90 - J91
識別
名稱	五角錐球狀屋頂 Disphenocingulum
別名	五角錐球形屋根（日語）
參考索引	J90
鮑爾斯縮寫 （verse-and-dimensions的wikia：Bowers acronym）	dawci
性質
面	24
邊	38
頂點	16
歐拉特徵數	F=24, E=38, V=16 （χ=2）
組成與佈局
面的種類	4+2×8個三角形 4個正方形
頂點圖	4個(32.42) 4個(35) 8個(34.4)
對稱性
對稱群	D2d群
特性
凸
圖像
（展開圖）

性質

五角錐球狀屋頂共由24個面、38條邊和16個頂點組成^[5][6][7][8]。其可以視為由2個去除2個三角形面的球狀屋頂三角形面重新排列合併而成，每個去除2個三角形面的球狀屋頂有12個面，三角形面重新排列合併完成後為二十四面體。其英文名稱字首「di-」表示兩個球狀屋頂，而字尾「-cingulum」（為belt（腰帶）的拉丁語）指的是12個分布於兩個正方形「屋頂」周圍的三角形的腰帶，兩者彼此旋轉90度互相接合^[7]。雖然這24個面皆為正多邊形，但由於其有多種頂角，不滿足點可遞的特性，因此不屬於均勻多面體，這類立體早在1966年由諾曼·詹森（英语：Norman Johnson (mathematician)）（Norman Johnson）命名並給予描述^[4]。

在組成五角錐球狀屋頂的24個面中，有20個三角形面和4個正方形面^[6][8]。在其16個頂點中，有4個是5個三角形的公共頂點^[8]，在頂點圖中可以用[3⁵]來表示^[9]、還有8個頂點是4個三角形和1個正方形的公共頂點，在頂點圖中可以用[3⁴,4]來表示^[9]、剩下的4個頂點是2個三角形和2個正方形的公共頂點^[8]，在頂點圖中可以用[3²,4²]來表示^[9]。

體積與表面積

若一個五角錐球狀屋頂邊長為${\displaystyle a}$，則其表面積${\displaystyle A}$為：^[10]

${\displaystyle A=4+5{\sqrt {3}}a^{2}\approx 12.6603a^{2}}$^[11]

在92種詹森多面體中，有13種詹森多面體的單位邊長體積（V/a³）無法表達為解析數。而五角錐球狀屋頂就是這13種詹森多面體之一。

由於其體積無法表達為解析數，但可以用近似值表示。邊長為${\displaystyle a}$的五角錐球狀屋頂體積近似為：

${\displaystyle V\approx 3.7776453418585752429a^{3}}$^[6]。

上述體積近似值為以下多項式的最大實根：^[12]

1213025622610333925376 x24 + 54451372392730545094656 x22 − 796837093078664749252608 x20 − 4133410366404688544268288 x18 + 20902529024429842816303104 x16 − 133907540390420673677230080 x14 + 246234688242991598853881856 x12 − 63327534106871321714442240 x10 + 14389309497459555704164608 x8 + 48042947402464500749392128 x6 − 5891096640600351061013664 x4 − 3212114716816853362953264 x2 + 479556973248657693884401

頂點座標

令${\displaystyle a}$ ≈ 0.76713為下列多項式的實根

${\displaystyle {\begin{aligned}&256x^{12}-512x^{11}-1664x^{10}+3712x^{9}+1552x^{8}-6592x^{7}\\&\quad {}+1248x^{6}+4352x^{5}-2024x^{4}-944x^{3}+672x^{2}-24x-23\end{aligned}}}$

和${\displaystyle h={\sqrt {2+8a-8a^{2}}}}$和${\displaystyle c={\sqrt {1-a^{2}}}}$。

則邊長為2的五角錐球狀屋頂可以由下列頂點的軌道的並集在沿xz平面和yz平面鏡射所產生的空間對稱群之群作用下給出：^[13]

${\displaystyle \left(1,2a,{\frac {h}{2}}\right),\ \left(1,0,2c+{\frac {h}{2}}\right),\ \left(1+{\frac {\sqrt {3-4a^{2}}}{c}},0,2c-{\frac {1}{c}}+{\frac {h}{2}}\right)}$

相關多面體

• 
  球狀屋頂
  （原始的球狀屋頂立體）
• 
  球狀屋頂欠側錐
  （移除一個五角錐的球狀屋頂）
• 
  側錐球狀屋頂
  （在正方形面疊上正四角錐的球狀屋頂）
• 
  加長型球狀屋頂
  （正方形附近的4個位置上各加上1個正三角形的球狀屋頂）
• 
  廣底加長型球狀屋頂
  （「屋頂」部分由3個正方形組成的球狀屋頂）
• 
  廣底加長型球狀屋頂欠側錐
  （移除一個五角錐的廣底加長型球狀屋頂）
• 
  五角錐球狀屋頂
  （合併兩個移除了兩個正三角形的球狀屋頂）

參見

• 詹森多面體
• 多面體