杜卜勒效應 （英文 ： Doppler effect ），又叫多普勒效應 ，係一種關於波動 嘅物理現象 ，講緊波源 （一股波動嘅源頭）同觀察者有相對嘅郁動 嗰陣，觀察者探測到嘅波頻率 會同波源發出嘅波頻率唔一樣：如果波源向住觀察者郁，觀察者接收到嘅波頻率會高咗，而如果波源係遠離緊觀察者，觀察者收到嘅波頻率就會低咗。
呢隻天鵝 周圍嘅水面波動 出現咗杜卜勒效應。 杜卜勒效應呢個概念响物理學 上幾重要。有唔少聲學 應用計數嗰陣，都要考慮埋杜卜勒效應嘅影響。除此之外，杜卜勒效應對宇宙學 亦有所啟示：簡化講，天文學家 分析由其他天體 射落地球 嘅光 ——光係電磁波 一種，佢哋發現呢啲天體似乎多數都係遠離緊地球嘅，而呢點係其中一項重要證據 ，表示宇宙依家正喺度膨脹緊 。
杜卜勒效應個諗頭最初係由奧地利 物理學家 杜卜勒 喺 1842 年提出來嘅[1] 荷蘭 化學家 白貝羅 畀一隊喇叭手企喺一架喺荷蘭烏德勒支 附近駛過嚟嘅敞篷火車 上面演奏 ，白貝羅佢喺月臺上面探測到音高 改變，確認咗杜卜勒效應嘅概念[2]
杜卜勒效應係一種有關波動 嘅現象。想像有一件物體（波源），佢响度發出一段段持續嘅聲波 [註 1]
f
{\displaystyle f}
頻率 ，呢股波嘅週期
T
{\displaystyle T}
[3]
T
=
1
f
{\displaystyle T={\frac {1}{f}}}
頻率 ：指一秒重複幾多次。週期 ：指重複一次要幾耐（以秒計）。假想依家有一位人類 觀察者喺度聽嗰股聲波，同時假設由始至終，聲波嘅頻率無論點變都冇離開人類嘅聽力範圍 。設波源同觀察者都係靜止唔郁（速度 同加速度 都係 0）嘅，觀察者接收到嗰一股波動，每兩個相鄰嘅高峰 （maxima [註 2] 粵拼 ：mek1 sim4 maa4 ）之間喺時間上都相差咗
T
{\displaystyle T}
波長
λ
{\displaystyle \lambda }
距離 ）就會係
λ
=
T
c
s
{\displaystyle \lambda =Tc_{s}}
T
=
λ
c
s
{\displaystyle T={\frac {\lambda }{c_{s}}}}
當中
c
{\displaystyle c}
音速 [註 3]
漣漪 （左圖）同
表面波 現象，可以想像成
水 粒子 受擾動上下來回噉郁（右圖嘅
抽象 圖解）。Maxima 係指粒粒子最高可以去到嗰個高度，因為呢股擾動係有週期（重重複複）嘅，每次遇到一個新嘅 maxima 就係重複咗次。因此，兩個相鄰嘅 maxima 之間相差嘅
時間 就係一次週期
T
{\displaystyle T}
。
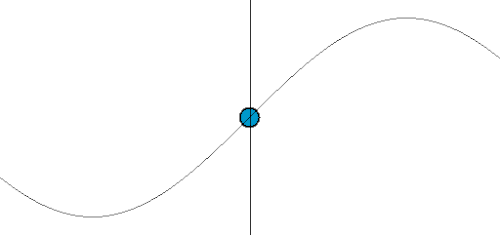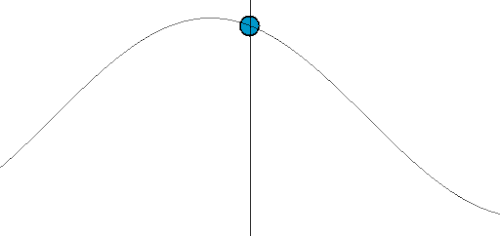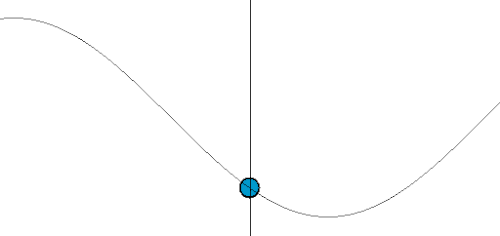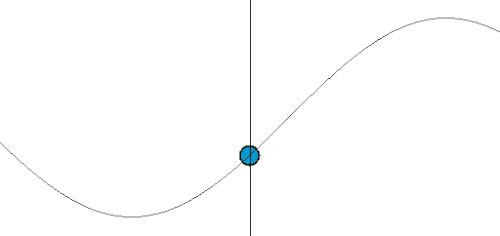
上述嘅過程用圖像 化嘅方式表達嘅話：
想像紅色點 係波源，個波源依家係唔郁嘅。
藍色線 係啲高峰嘅位置。幅圖 X Y 兩條軸分別表示啲嘢嘅 X Y 座標 位置。
設觀察者身處 (10, 0) 嗰個位。
假如觀察者都係靜止唔郁嘅，佢感受到嘅波動頻率（由相鄰藍色線 之間嘅時間差反映），同波源所發出嘅一樣。
杜卜勒效應動畫：
紅色嘅圓圈 代表聲波啲高峰嘅位置，由上圖睇得出，隨住架
車 （聲波嘅源頭）
郁動 ，會令到啲聲波由左邊聽起嚟頻率高咗，又會令啲聲波由右邊聽起嚟頻率低咗。
呢段聲係一架車一路經過觀察者一路
響咹 ；架車經過前經過後發出嘅聲，
音高 （音高反映頻率）聽落唔同咗。
依家想像一個波源一路發出聲波一路開始郁，同時觀察者繼續企定定唔郁。波源嘅速度 係
v
{\displaystyle v}
λ
{\displaystyle \lambda }
T
a
{\displaystyle T_{a}}
λ
a
{\displaystyle \lambda _{a}}
T
a
=
λ
a
c
s
{\displaystyle T_{a}={\frac {\lambda _{a}}{c_{s}}}}
T
a
=
(
c
s
−
v
c
s
)
T
{\displaystyle T_{a}=({\frac {c_{s}-v}{c_{s}}})T}
噉即係話觀察者睇到嗰個頻率（
f
a
{\displaystyle f_{a}}
f
a
=
1
T
a
=
(
c
s
c
s
−
v
)
1
T
=
(
c
s
c
s
−
v
)
f
{\displaystyle f_{a}={\frac {1}{T_{a}}}=({\frac {c_{s}}{c_{s}-v}}){\frac {1}{T}}=({\frac {c_{s}}{c_{s}-v}})f}
即係話嗰股聲波嘅頻率，聽落會高咗[註 4] 聽覺 系統嚟講，一段聲波嘅頻率高咗最明顯嘅體現係「聽落高音咗 」。而如果個聲波源嘅郁動方向係相反，離觀察者愈嚟愈遠嘅話，都可以用噉嘅道理嚟諗，
f
a
{\displaystyle f_{a}}
f
a
=
(
c
s
c
s
+
v
)
f
{\displaystyle f_{a}=({\frac {c_{s}}{c_{s}+v}})f}
即係話嗰股聲波嘅頻率，聽落會低咗，而對人類嘅聽覺系統嚟講，一段聲波嘅頻率低咗最明顯嘅體現係「聽落低音咗 」[3] 古典物理學 當中嗰條基本式如下：
f
a
=
(
c
±
v
r
c
±
v
s
)
f
0
{\displaystyle f_{a}=\left({\frac {c\pm v_{\text{r}}}{c\pm v_{\text{s}}}}\right)f_{0}}
當中
v
s
{\displaystyle v_{\text{s}}}
v
r
{\displaystyle v_{\text{r}}}
f
0
{\displaystyle f_{0}}
f
a
{\displaystyle f_{a}}
[4]
用圖像化嘅方式表達。波源開始郁，但
v
s
<
c
{\displaystyle v_{s}<c}
想像波源開始向右郁，而觀察者企咗喺波源嘅右邊（例如 (10,0) 嗰個位）。
當波源發放出一個新嘅波高峰（藍色線 ）嗰陣，因為佢向右郁緊，所以新高峰同前一個向右邊射出去嘅高峰之間距離（觀察者睇到嘅波長）望落好似短咗噉，短咗
v
s
T
{\displaystyle v_{s}T}
λ
a
{\displaystyle \lambda _{a}}
λ
a
=
λ
−
v
s
T
{\displaystyle \lambda _{a}=\lambda -v_{s}T}
如果觀察者企咗喺波源嘅左邊（例如 (-10,0) 嗰個位；佢離波源愈嚟愈遠），波長望落就會長咗。
v
s
=
c
{\displaystyle v_{s}=c}
假想波源而家以音速咁快嘅速度郁，而佢發出嗰股波依然係聲波。
佢發出嗰啲波高峰會「結合埋一齊」，如果觀察者企喺 (10,0) 嗰個位，佢會咩都聽唔到——直至波源一嘢撞落佢度嗰一刻，佢至感受到嗰股波。
如果觀察者企咗喺波源嘅左邊（例如 (-10,0) 嗰個位；佢離波源愈嚟愈遠），波長望落會長咗。
v
s
>
c
{\displaystyle v_{s}>c}
依家波源嘅速度係
1.4
c
{\displaystyle 1.4c}
如果觀察者企喺 (10,0) 嗰個位，佢會睇到波源經過佢，然後先至聽到波源發出嘅聲。
如果觀察者企咗喺波源嘅左邊（例如 (-10,0) 嗰個位；佢離波源愈嚟愈遠），波長望落會長咗。
可見光 （人眼睇得到嘅光 ）係一種電磁波 （EM wave），噉講意思即係光嘅傳播涉及咗電磁場 嘅振盪 。可見光嘅波長處於 380 納米 至 700 納米之間。實證嘅研究早已顯示，一束光望落咩色 ，取決於佢嘅波長，波長高嘅就偏向紅色 ，而波長低嘅就偏向藍色 同紫色 ，波長太高嘅話嗰股電磁波就會變成紅外線 ，而波長太低嘅話就會變成 UV [5]
以下係可見光譜 ，左邊係低頻（波長高）嘅可見光，偏向紅色，而右邊係高頻（波長低）嘅可見光，偏向藍同紫色：
呢幅相入便嘅係哈勃太空望遠鏡 。 想像家陣天文學家 用望遠鏡 （好似哈勃太空望遠鏡 咁勁嗰啲）觀察地球 周圍嘅太空 ，睇到無數咁多粒恆星 ，呢啲恆星射出嘅光穿過咗閒閒哋幾十幾百光年 （1 光年超過 9.46 × 1012 公里 ）咁遠嘅距離先嚟到太陽系 ，最後射落去天文學家嘅望遠鏡嗰度畀佢哋觀察到。天文學家可以剖析呢啲光嘅波長，然後就會有最少兩個可能性[3] :p 4 ：
紅移 （redshift）：佢哋觀察到嘅光，慢慢偏咗去紅色，而慢慢偏向紅色即係話束光嘅波長長咗，顯示發出嗰束光嘅物體離地球愈嚟愈遠。藍移 （blueshift）：佢哋觀察到嘅光，慢慢偏向藍同紫色，而噉亦即係話嗰束光嘅波長變短咗，顯示發出嗰束光嘅物體離地球愈嚟愈近。天文學家睇勻太空當中咁多唔同嘅天體，發現咗一個重要嘅線索：呢啲天體發出嘅光近乎全部都喺度紅移緊 ，仲要係離地球愈遠嘅就紅移得愈勁。而且紅移嘅幅度
z
{\displaystyle z}
z
=
1
c
H
0
r
{\displaystyle z={\frac {1}{c}}H_{0}r}
當中
c
{\displaystyle c}
光速 ，
H
0
{\displaystyle H_{0}}
哈勃常數 ，而
r
{\displaystyle r}
哈勃定律 ，呢條式對宇宙學 知識產生咗重大嘅影響——响廿世紀初，科學界 仲喺度拗「到底宇宙係膨脹緊，抑或係收縮緊 」噉嘅問題，而哈勃定律嘅發現就係其中一個關鍵證據 ，支持咗「宇宙係喺度膨脹緊」呢一個諗法[6]
就算將「聲波」換做光 、表面波 或者其他波動 ，下面講嘅原理都可以用同樣嘅方法嚟諗。 要廣義化 （適用於其他波動同介質 ）嘅話，
c
{\displaystyle c}
呢條式有明顯漏洞——假如波源正喺度迫近而
c
s
=
v
{\displaystyle c_{s}=v}
音爆 等嘅現象。
Alec Eden The search for Christian Doppler , Springer-Verlag, Wien 1992.
Jonkman, E. J. (1980). "Doppler research in the nineteenth century". Ultrasound in Medicine & Biology . 6 (1): 1-5.
Rosen, Joe; Gothard, Lisa Quinn (2009). Encyclopedia of Physical Science . Infobase Publishing. p. 155.
Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences . 15 (3): 168-173.
