數織
来自维基百科,自由的百科全书
數織是一種邏輯遊戲,以猜謎的方式繪畫黑白點陣圖。在一個網格中,每一行和列都有一組數,玩家需根據它們來填滿或留空格子,最後就可以由此得出一幅圖畫。例如,「4 8 3」的意思就是指該行或列上有三條獨立的線,分別佔了4、8和3格,而每條線最少要由一個空格分開。傳統上,玩家是以黑色填滿格子,和以「×」號標記一定不需要填充的格子。數織是一個NP完全的問題。
此條目沒有列出任何參考或來源。 (2017年4月29日) |
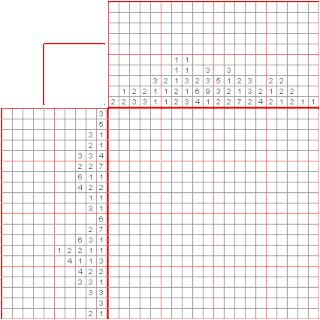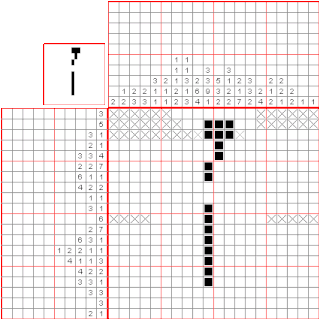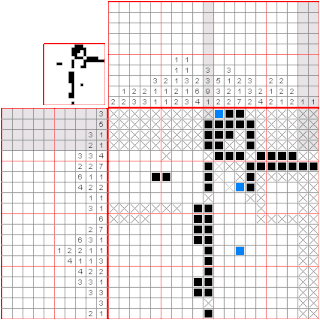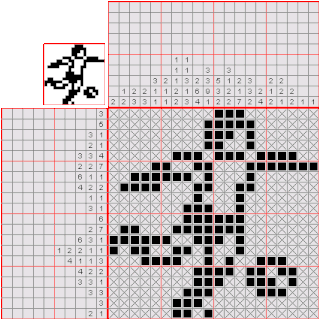


數織是在1987年由日本人西尾徹也發明的。數織的日文名稱是「お絵かきロジック」,意思是「繪畫邏輯」。數織初見於日本的解謎者雜誌,玩家用紙和筆來玩。隨後,任天堂以「Mario's Picross」為名推出了兩款Game Boy和九款超級任天堂遊戲。現時任天堂DS上亦有名為Picross DS的同款遊戲。2015年十二月,任天堂推出了名為「Pokémon Picross」的3DS遊戲。
名字
Nonogram有著許多不同的名字,包括Paint by Numbers、Griddlers、Pic-a-Pix、Picross、Pixel Puzzles、Crucipixel、Edel、FigurePic、Grafilogika、Hanjie、Illust-Logic、Japanese Crosswords、Japanese Puzzles、Kare Karala!、Logic Art、Logic Square、Logicolor、Logik-Puzzles、Logimage、Zakókodované obrázky、Maľované krížovky、Oekaki Logic、Oekaki-Mate、Paint Logic、Shchor Uftor和Tsunami。
Nonogram至今還未有正式或廣泛流傳的中文名稱,已知的中文名有:數織、數牆、填方塊、發現小花、邏輯拼圖、津波拼圖、數塗[1]等。
解謎技巧
玩家可以利用數組盡量的填充格子。
如果數字等於行高或列寛的話,該行所有格子都要填滿。
如果不是的話,玩家則可以假設每條線只有由一個空格分隔,把線組推到可移動的空間的最盡;然後,把線組推到另一個盡頭。兩者重疊的填充部份就是一定要填充的格子。
例如:
| 8 | ||||||||||
| 8 |
可得出這結論:
| 8 |
又例如:
| 4 3 | ||||||||||
| 4 3 |
可得出這結論:
| 4 3 |
除了盡量的填充之外,玩家亦可以把一定不可能要填上的空格用「×」號標記起來,從而減少需要考慮的格子。
如果數字是零的話,該行所有格子都需留空(玩家可用「×」號標上)。
即使不是零,玩家也可以根據已填充的格子,把線推到可移動的空間的最盡,再把線推到另一盡頭。兩者重疊的留空部份就是一定不需要填上的空格。
假設玩家因為之前的推算,現已得出以下結果:
| 3 1 |
如果把線填滿,可以有以下兩個極端的可能性:
| 3 1 | ||||||||||
| 3 1 |
因此可得出這結論:
| 3 1 | × | × | × | × |
又如果該行或列中有些空格已經不足之放上任何一條線,那些空格也是可以標空的。例如:
| 3 | × | × |
玩家可以不用考慮右邊的空格:
| 3 | × | × | × | × | × | × |
如果兩條鄰近的線由一個空格分隔的話,玩家可以用以下的推論嘗試把它填充或標空:
- 如果把它們連接起來,會令線條過長的話,該空格應該標空。
- 如果把它們分隔,會令線條數目過多的話,該空格應該填充。
例子如下:
| 5 2 2 |
經過推論後:
| 5 2 2 | × |
因為需要盡量的填充和標空,聰明的玩家在這例子可能會直接跳到這步:
| 5 2 2 | × | × | × | × | × | × |
在一些難度較高的遊戲中,玩家可能不能利用以上簡單的推論方法來解謎。這時玩家可以先假定一個空格為需要填上的,然後繼續解答。但當遇到矛盾的話,玩家需要把遊戲回退到假定前的狀態,因為矛盾証明了之前的假定是錯誤的。玩家亦可把該空格標空,因為它一定不是需要填充的格了。
多重答案
有些數織可以有多個可行的答案(踩地雷也會有這種情況)。不過並不是所有答案都是有意思的圖像。
一個簡單的例子就是以數織記錄的西洋棋棋盤。為了方便閱讀和編輯,以下的棋盤大小只是平常的四分之一。
答案一:
| 1 1 |
1 1 |
1 1 |
1 1 | |
| 1 1 | × | × | ||
| 1 1 | × | × | ||
| 1 1 | × | × | ||
| 1 1 | × | × |
答案二:
| 1 1 |
1 1 |
1 1 |
1 1 | |
| 1 1 | × | × | ||
| 1 1 | × | × | ||
| 1 1 | × | × | ||
| 1 1 | × | × |
變種
也有一種彩色版的邏輯拼圖遊戲,謎題中有多種顏色的色塊,並從而取消了傳統黑白版(英語:R&B)中的空白格設計。
外部連結
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
