Remove ads
替換式密碼，又名取代加密法[1]，是密碼學中按規律將文字加密的一種方式[2]。替換式密碼中可以用不同字母數為一單元，例如每一個或兩個字母為一單元，然後再作加密。密文接收者解密時需用原加密方式解碼才可取得原文本。由於拼音文字中字的組成為有限的字母，以英語為例只有26個字母，組成可能的單元數較少，因此使用替換式密碼相對較為容易，而且亦可使用簡單機械進行加密；相反，非拼音文字如中文則因單元數非常大難以使用一般加密方式，必需建立密碼本，然後逐字替換。更何況某些非拼音文字中字字皆由不同大小的字根來組字，較難轉換，因此使用替換式密碼的示例比較少。
 | 此條目需要補充更多來源。 (2016年9月25日) |
但對比還是很難。
當以替換式密碼與置換式密碼（或稱轉位式密碼或移轉式密碼[3]:1-15）相比較時，可以發現轉位式密碼只是改變明文中單元的位置，而單元本身沒有轉變；相反，替換式密碼只是轉換單元，但密文中單元的位置沒有改變[4]:13。
替換式密碼亦有許多不同類型。如果每一個字母為一單元（或稱元素[2]）進行加密操作，就可以稱之為「簡易替換密碼」（英語：simple substitution cipher）或「單表加密」（英語：monoalphabetic cipher）[4]:13，另又稱為單字母替換加密；以數個字母為一單元則稱為「多表加密」（英語：polyalphabetic cipher）[4]:13或「表格式加密」（英語：polygraphic）。單表加密只可在一個單元中使用同一種替換加密，而多表加密則可在一個單元使用不同的加密方式，明文單元映射到密文上可以有好幾種可能性，反之亦然[4]:13。
Remove ads
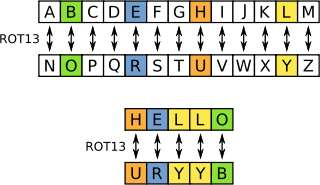
簡易替換加密是一種以特定方式改變字母表上字母順序，並以此順序書寫的加密方式。這樣一張改變了字母次序的字母表即為『替換表』。替換表可以以偏移或逆轉（分別為凱撒密碼和阿特巴希密碼（英語：Atbash））或更複雜方式構造，此時稱之為『混合表』。傳統上會先把一個關鍵詞寫在字母表最前面，再刪去重複字母，這樣就能得到一個混合表。
使用混合表系統，關鍵字為「zebras」：
| 明文為 | ABCDEFGHIJKLMNOPQRSTUVWXYZ |
| 密文為 | ZEBRASCDFGHIJKLMNOPQTUVWXY |
明文為：
flee at once. we are discovered!
加密結果為：
SIAA ZQ LKBA. VA ZOA RFPBLUAOAR!
傳統上，密文會省略標點符號和空格，同時會有一固定長度的單位，以避免傳輸錯誤和變相顯示明文中單詞的邊界。這些單位被稱為「組」（英語：groups）[4]:13，有時叫「組數」（英語：group count）（即組的數量），並使其作為一額外檢查。通常都會使用五個字母為一組[4]:17[5]，然後使用電報傳送消息：
SIAAZ QLKBA VAZOA RFPBL UAOAR
如果該段明文的長度不能被五整除，將需要在最後用「NULL」補齊[3]:1-7。這些空字符可以是任何字符，因為解密後可以看出是明顯的廢話（如ORANG EOOOO），所以接收器可以很容易地發現並將其丟棄。如若接收發現密文的長度不能被五整除，就可以得知傳輸出錯，並要求重新發送。
簡易替換密碼有時不一定要替換至另一字母，例如在豬圈密碼中，密文由格子的符號組成。例子如下：[6]
這些功能增加的安全性與以前其實相差不大，因為基本上所有奇怪的符號最後都會轉換成A-Z字母。
有時銷售人員會在他們的名單和目錄中使用非常簡單的加密法：用字母來代替數字。
| 本文（數字）： | 1234567890 |
| 加密字母： | MAKEPROFIT [7] |
例子：MAT代表120。
Remove ads
簡易替換密碼的缺點是字母表中的最後幾個字母（其中大多是低使用頻率）往往留在最後。加強的辦法是在加密後再做一次縱欄式移調，但很多時也沒有這樣做。
儘管加密用到的密鑰可能性很大（26! ≈ 288.4，若88位元），但要破解單表加密卻異常容易。只要提供有合理長度的密文（見下文），密碼分析就能通過頻率分佈的分析推斷最常見的單元的意義，即頻率分析。這使破解者可用剔除法，把有個單元的意思解出來，見一個破解的例子。在某些情況下，可以從它們的字母的格局來破解，例如「attract」和「osseous」是英語中僅有的「ABBCADB」模式的「根」，即如遇見有簡易替換密碼的密文中出現「ABBCADB」，即可猜測其為「attract」或「osseous」。康樂及報紙拼圖等包含著不少這種加密法。
按照英語的單一性距離，密文平均最少需要27.6個字母才能破解混合表簡易替換密碼[8]。而在正常情況下，假設遇到的是新排列方式，但通常都需要約50個字母（當中有些密文可以用得比較少）。然而，當密文有極平坦的頻率分佈，密文長度的需求可能越來越大。同時，加密者可以添加空字元來造成平坦的頻率分佈。
另外，有另一種方法來「偽造」頻率分佈，名為漏字文。顧名思義，這些文章會有意避免使用某個或某幾個特定字母。如果漏掉的是E，那麼若然繼續以正常的頻率分析（估計最高頻率者為E）就不可能找出真正的明文。
Remove ads
早期的加密中，為增加替換式密碼應付頻率分析攻擊的強度，有時會採用「諧音」來改變明文字母頻率。在這種加密算法中，明文字母可以映射到多個密文符號。通常情況下，頻率最高的明文符號（如E）會比低使用頻率的字母（如X）有更多的諧音符號，使頻率分佈更為平坦，讓分析更困難。
但亦因此，只是字母之間互相替換就會造成不夠分配，從而有了好幾種不同的解決方法。其中最簡單的方式可以算是用1-0共10個數字作為某些字母的替換。另一種方法則是將現有的字母分開成原字母配以簡單的變化、大寫、小寫、上下倒轉的字母、鏡像文字（左右倒轉）等。雖然更為藝術化，卻不代表一定更安全，其中一些諧音替換法全部使用新發明的奇特符號來代表字母。（參見伏尼契手稿以及愛倫·坡所著的金甲蟲）
一種有趣的變化名為命名密碼法[3]:1-8。此加密法有許多不同的版本，之間的區別來自其前綴。而該前綴來自宣讀來訪貴賓稱號的公職人員名字。這種密碼結合一個小型密碼本組成一個大型的諧音替換表。在此密碼中，常用單詞會按密碼本加密，餘下字母則按另一本密碼本加密，兩者符號最後在密文中混起來，以減低簡易替換密碼中被破解的風險[3]:1-8。路易十四所使用的密碼是羅西諾爾家族創立的偉大密碼，該密碼直至法國王室廢止後百年才被破解。
15世紀早期至18世紀後期，命名密碼是外交文件及間諜最常使用的加密，然而其中大多數仍然使用加密性能較差的命名密碼。雖然由十六世紀中葉開始政府情報機構的密碼分析員就破解部分命名密碼法，但使用者通常的反應僅僅
是加大諧音替換表。十八世紀後期，諧音替換系統開始消亡之時，一些命名密碼已有高達5萬個符號。
然而，並非所有命名密碼法都已被破解。直到今天，仍然不時有新的命名密碼被破解的新聞。
比爾密碼是另一個諧音替換法的例子。這個故事指在1819年至1821年期間由一個加密文本來隱藏美國獨立宣言中所述的寶藏。在這裡，每個密文字元由一個數字替換。數字代表著獨立宣言中第幾個字的第一個字母。獨立宣言中許多字的首字母都是一樣的，而密文數字能是其中任何一個，例如正文中第二和第六個字都是「I」開頭，即「I」既可以是2，又可以是6。而解讀僅僅就是把密文中的數字（如代數X），放到獨立宣言中查找（第X個字的首字母）。
斯塔爾則描述了另一個諧音替換密碼[9][10]，其密碼是第一次嘗試在電腦的資料庫上加密。在斯塔爾的方法中，無論是明文還是密文都是以二進制字符串存儲，因此諧音的數量可以非常大，使得頻率分析比平常更為困難。
Remove ads
在1467年，多表替換密碼由萊昂·巴蒂斯塔·阿爾伯蒂以圓碟的形式首次描述。約翰尼斯·特里特米烏斯所著的《隱寫術》（古希臘語：Steganographia）中介紹了一種表格（見下；15世紀已完成但很久以後才出版[11]）。1563年，喬瓦尼·巴蒂斯塔·德拉波爾塔在《書寫中的隱蔽字符》（古希臘語：De Furtivis Literarum Notis）描述了一個更複雜的混合字母版本[12]:139。
在一個多表替換密碼中，會使用多個字母作為密碼。為了加快加密或解密速度，所有的字母通常寫在一張表格上，密碼學上稱作tableau。這種表格通常是26×26，因為這樣才能放下全部26個英文字母。填充表格及選擇下次使用的字母的方法，就是不同多字母替換密碼之間的定義。多字母替換密碼比單字母更難打破，因為其替換可能性多，密文要較長才可。
其中最著名的一種為吉奧萬·巴蒂斯塔·貝拉索於1585年推出的維吉尼亞密碼[4]:34。它於1863年之前一直未被破解。法國人稱它作「不能破譯的密碼」（法語：le chiffre indéchiffrable）。（此密碼曾被誤以為由布萊斯·德·維吉尼亞所創[12]:On the Origin of a Species，所以才叫作維吉尼亞密碼。）
維吉尼亞密碼中，表格的第一行只需直接填上26個字母，然後以下每一行的字母都是向左偏移一格。（這叫作表格橫移，數學上每一列同餘26。）要用這種密碼需要使用一個關鍵字來作為密鑰。關鍵字每次用完就再次重複。假設關鍵字是「CAT」，明文的第一個字由「C」加密，第二個字由「A」加密，第三個則由「T」加密，然後再回到C加密，一直重複。然後按照右邊的密碼表加密，例如BALL用CAT作關鍵字時會加密至DAEN，可見即使是同一個「L」亦會加密至另一個字母。現實中，維吉尼亞密碼的關鍵字非常長。
1863年，弗里德里希·卡西斯基少校發明了一種方法（在克里米亞戰爭前已由查爾斯·巴貝奇秘密並獨立地發明[13][14]），使得可以計算維吉尼亞密碼中關鍵字的長度[4]:37。這種方法需要較長的密文，因為其運作依靠找出常見的字（如THE）使用相同關鍵字（如ABC）的數量，因此，極短的密文難以用此辦法找出。
因此，即使在今天，如果在表格中使用混合表加密，或關鍵字是隨機的，維吉尼亞密碼理論上亦難以破解。但由於實際上很難用到這些方法，維吉尼亞密碼的使用越來越少。
其他著名的多字母替換加密包括：
- 格蘭示菲特密碼 - 與維吉尼亞密碼相似，但由於整個密碼只使用10個單元，因此關鍵字長度有限，很容易被破解。
- 博福特密碼 - 這實際上就是維吉尼亞密碼，除「tabula」改為向後偏移一格，數學上是等式為：密文＝鍵－明文。博福特密碼屬於對等加密，即加密算法與解密算法相同[4]:34。
- 自動密鑰密碼 - 它的密鑰開頭是一個關鍵詞，之後則是明文的重複，以避免周期函數。
- 運動密鑰密碼，關鍵詞從某些文章或名句中取出，因此可以非常長。
現代的流密碼中可以看出，現代的多表替換加密都努力改進流密鑰，使其盡可能的長及不可預知。
Remove ads
在表格式替換密碼中，明文不再單獨替換某個字母，而是一次過替換較大的字母單元（通常為一對字母）。第一個優點是頻率分佈比單個字母時更平坦（雖然實際上並不平坦，因為在日常語言中，「TH」就遠遠比「XQ」常見）。其次，其產生的大量的符號，相應地需要更多的密文來進行高效的字母頻率分析[來源請求]。
為了替換每「對」字母，將需要共676個符號（）。在之前說過的《書寫中的隱蔽字符》一書中，德拉波爾塔提出了這樣一個系統：用一個20 x 20的表格（義大利或拉丁文字中的20個字母。），其中填上400個特別的字形。然而，該系統實為不切實際，更有可能從來沒有實際使用過[來源請求]。
最早的實用表格式替換密碼是查爾斯·惠斯登爵士於1854年所創的波雷費密碼。在此密碼中，5×5的方格中填滿了混合字母（兩個字母，通常I和J並排，即I等於J）。明文中每兩個字母為一單元，通常這個單元會在表上組成一個四方形（單元內容佔其中兩個角），然後取另外兩角為密文。當單元內容在同一列或同一行時（即無法組成四方形），同列者密文為明文往右偏移一格；同行者密文為明文往下偏移一格。單元中兩者為同字母者於該單之前添加X（或Q）（即其後全體往後偏移一格）。波雷費密碼於第二次波耳戰爭開始直到第二次世界大戰為止一直用於軍事用途[4]:26。
在1901年，費利克斯·第利斯塔推出了其他一些實際可用的表格式替換加密，包括二分密碼、四方密碼及三分密碼[來源請求]。
萊斯特·S·希爾於1929年發明了希爾密碼，它是一種表格式替換加密。希爾密碼可以使用線性代數來結合擁有非常多字母的單元。每個字母被視為二十六進制的數字：A = 0，B = 1，依此類推。（在某些變種中，會添加3個額外符號，將基底變成一個質數。）一串字母當成n維向量，跟一個n×n的矩陣相乘，再將得出的結果同餘26。注意用作加密的矩陣（即密匙）在必須是可逆的，否則就不可能解碼。只有矩陣的行列式和26互質，才是可逆的[來源請求]。
因為希爾密碼完全建基於線性關係上，它會很容易受到己知明文攻擊，因此，有時它會結合一些非線性步驟來減少被擊破的機會[來源請求]。
Remove ads
從第一次世界大戰時期開始，直到電腦被廣泛使用（某些政府約在20世紀50至60年代開始使；其他組織在十年或更後，1975年前則未有個人使用的紀錄），多字母替換密碼一直在機械上被廣泛應用。幾位發明家於同一時間有著類似的想法，1919年間已有四次關於旋轉盤的專利申請。其中最重要並著名的可算是德意志國防軍於1930年代所用的恩尼格瑪密碼機[15]。同時期盟軍亦有其加密系統：美國的Sigaba及英國的Typex[來源請求]。
它們的相似之處在於它們都使用機械式旋轉盤來加密。由於不止一個旋轉盤的組成密文，如果每個字皆配一符號，符號用量將高於天文數字。然而，這些機器的早期版本極易被破解。信號情報服務處的威廉F.弗里德曼威廉·F·弗里德曼於早期就發現了赫本旋轉器的漏洞；政府密碼學校的第利溫·諾克斯在第二次世界大戰前就破解了恩尼格瑪密碼機中沒有接線板的版本。布萊切利園的分析員在後期才能破解恩尼格瑪密碼機的軍用版本，其靈感來自波蘭數學家馬里安·雷耶夫斯基[來源請求]。
SIGABA與Typex加密的訊息民間則至今沒有被破解的消息[來源請求]。
Remove ads
一次性密碼本是一種頗特別的替換密碼。它由約瑟夫·馬賓於第一次世界大戰後期建立[16][17]。克勞德·夏農約在第二次世界大戰期間，在數學上證明它的保密性牢不可破[18]，其過程於1940年末首次出版。在常見的做法中，一次性密碼本可以被稱為一個單次替換密碼。通常情況下，明文字母將以某種方式（通常為邏輯異或[2]）與關鍵字組合（而不是替換掉）[19]。
一次性密碼本在大多數情況下都是不切實際或難以使用，因為它需要關鍵字跟明文一樣（或更）長、「完全」隨機、只能使用一次，更要保證除了發送者和接收者之外其它所有人都不知道。當這些條件有一項沒有執行，甚至只是極其輕微的違反，一次性密碼本便再也不是堅不可摧，甚至一觸即潰。美國曾於第二次世界大戰期間用非隨機的一次性密碼本加密訊息，再將其送往蘇聯。美國的密碼學家於40年代開始就能破解極少數一次性密碼本。（見維諾那計劃[20]）
上述的替換式密碼，尤其那些是只需使用鉛筆和紙張的手動加密密碼，都不再經常使用。然而，即使到了今天，替換加密的概念仍在進步。從一個夠新奇的角度來看，現代位元導向式的分組密碼（如資料加密標準及高階加密標準）仍可視為使用大量二進制字母的替換加密。此外，分組密碼通常包含較小的替換表，名為S-box[3]:3-14，其同時包含邏輯異或算法[3]:3-14。參見替換網絡。
- 夏洛克·福爾摩斯中的跳舞小人，其用跳舞小人替換英語，福爾摩斯最後根據分析字母頻率來破解密碼[21]。
- 最終幻想X中斯畢拉世界的語言實際上是一種替換密碼，其發音方法卻同為拉丁系統（例如你在英語中是you，然後加密至oui，再以法語來讀出oui）[22]。
- 乃出個未來中外星人的語言的符號全由英文替換加密而成。觀眾相當快就破譯出來，過程是在「Slurm」（外星人字）和「Drink」（英語）之間找到其密鑰[23]。後來，生產商建立了第二套外星人語言，其使用了數學密碼的更換和組合[24]。然而，此密碼再一次遭破譯，方法是將英語轉為1至26，轉換之後再加上前一個字母的編號，再同餘26（亦即代表前字母為Z時後字母不會加密）[24]。這些加密訊息可以從整個系列中每一集和其隨後推出的電影中看出。
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
Remove ads