雜湊函式（英語：Hash function）又稱雜湊演算法，是一種從任何一種資料中建立小的數字「指紋」的方法。雜湊函式把訊息或資料壓縮成摘要，使得資料量變小，將資料的格式固定下來。該函式將資料打亂混合，重新建立一個叫做雜湊值（又叫雜湊值）（hash values，hash codes，hash sums，或hashes）的指紋。雜湊值通常用一個短的隨機字母和數字組成的字串來代表。[1]好的雜湊函式在輸入域中很少出現雜湊衝突。如果在雜湊表和資料處理中，不抑制衝突來區別資料，會使得資料庫記錄更難找到。
如今，雜湊演算法也被用來加密存在資料庫中的密碼（password）字串，由於雜湊演算法所計算出來的雜湊值（Hash Value）具有不可逆（無法逆向演算回原本的數值）的性質，因此可有效的保護密碼。
雜湊函式的性質
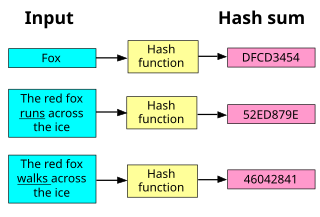
所有雜湊函式都有如下一個基本特性：如果兩個雜湊值是不相同的（根據同一函式），那麼這兩個雜湊值的原始輸入也是不相同的。這個特性是雜湊函式具有確定性的結果，具有這種性質的雜湊函式稱為單向雜湊函式。但另一方面，雜湊函式的輸入和輸出不是唯一對應關係的，如果兩個雜湊值相同，兩個輸入值很可能是相同的，但也可能不同，這種情況稱為「雜湊碰撞（collision）」，這通常是兩個不同長度的輸入值，刻意計算出相同的輸出值。輸入一些資料計算出雜湊值，然後部分改變輸入值，一個具有強混淆特性的雜湊函式會產生一個完全不同的雜湊值。
典型的雜湊函式都有非常大的定義域，比如SHA-2最高接受(264-1)/8長度的位元組字串。同時雜湊函式一定有著有限的值域，比如固定長度的位元串。在某些情況下，雜湊函式可以設計成具有相同大小的定義域和值域間的單射。在密碼學中，雜湊函式必須具有不可逆性。
雜湊函式的應用
由於雜湊函式的應用的多樣性，它們經常是專為某一應用而設計的。例如，加密雜湊函式假設存在一個要找到具有相同雜湊值的原始輸入的敵人。一個設計優秀的加密雜湊函式是一個「單向」操作：對於給定的雜湊值，沒有實用的方法可以計算出一個原始輸入，也就是說很難偽造。為加密雜湊為目的設計的函式，如SHA-2，被廣泛的用作檢驗雜湊函式。這樣軟體下載的時候，就會對照驗證代碼之後才下載正確的檔案部分。此代碼不會因為環境因素的變化，如機器組態或者IP位址的改變而有變動。以保證原始檔的安全性。
錯誤監測和修複函數主要用於辨別資料被隨機的過程所擾亂的事例。當雜湊函式被用於校驗和的時候，可以用相對較短(但不能短於某個安全參數, 通常不能短於160位元)的雜湊值來驗證任意長度的資料是否被更改過。
雜湊值可用於唯一地識別機密資訊。這需要雜湊函式是抗碰撞(collision-resistant)的，意味著很難找到產生相同雜湊值的資料。雜湊函式分類為密碼雜湊函式和可證明的安全雜湊函式。第二類中的函式最安全，但對於大多數實際目的而言也太慢。透過生成非常大的雜湊值來部分地實現抗碰撞。例如，SHA-256是最廣泛使用的密碼雜湊函式之一，它生成256位元值的雜湊值。
訊息或資料的接受者確認訊息是否被篡改的性質叫資料的真實性，也稱為完整性。發信人通過將原訊息和雜湊值一起傳送，可以保證真實性。
雜湊表是雜湊函式的一個主要應用，使用雜湊表能夠快速的按照關鍵字尋找資料記錄。（注意：關鍵字不是像在加密中所使用的那樣是秘密的，但它們都是用來「解鎖」或者訪問資料的。）例如，在英語字典中的關鍵字是英文單詞，和它們相關的記錄包含這些單詞的定義。在這種情況下，雜湊函式必須把按照字母順序排列的字串對映到為雜湊表的內部陣列所建立的索引上。
雜湊表雜湊函式的幾乎不可能/不切實際的理想是把每個關鍵字對映到唯一的索引上（參考完美雜湊），因為這樣能夠保證直接訪問表中的每一個資料。
一個好的雜湊函式（包括大多數加密雜湊函式）具有均勻的真正隨機輸出，因而平均只需要一兩次探測（依賴於裝填因子）就能找到目標。同樣重要的是，隨機雜湊函式不太會出現非常高的衝突率。但是，少量的可以估計的衝突在實際狀況下是不可避免的（參考生日悖論或鴿洞原理）。
在很多情況下，heuristic雜湊函式所產生的衝突比隨機雜湊函式少的多。Heuristic函式利用了相似關鍵字的相似性。例如，可以設計一個heuristic函式使得像FILE0000.CHK, FILE0001.CHK, FILE0002.CHK，等等這樣的檔名對映到表的連續指標上，也就是說這樣的序列不會發生衝突。相比之下，對於一組好的關鍵字效能出色的隨機雜湊函式，對於一組壞的關鍵字經常效能很差，這種壞的關鍵字會自然產生而不僅僅在攻擊中才出現。效能不佳的雜湊函式表意味著尋找操作會退化為費時的線性搜尋。
使用一個雜湊函式可以很直觀的檢測出資料在傳輸時發生的錯誤。在資料的傳送方，對將要傳送的資料應用雜湊函式，並將計算的結果同原始資料一同傳送。在資料的接收方，同樣的雜湊函式被再一次應用到接收到的資料上，如果兩次雜湊函式計算出來的結果不一致，那麼就說明資料在傳輸的過程中某些地方有錯誤了。這就叫做冗餘校驗。
校正錯誤時，至少會對可能出現的擾動大致假定一個分布模式。對於一個資訊串的微擾可以被分為兩類，大的（不可能的）錯誤和小的（可能的）錯誤。我們對於第二類錯誤重新定義如下，假如給定H（x）和x+s，那麼只要s足夠小，我們就能有效的計算出x。那樣的雜湊函式被稱作錯誤校正編碼。這些錯誤校正編碼有兩個重要的分類：迴圈冗餘校驗和里德-所羅門碼。
對於像從一個已知列表中匹配一個MP3檔案這樣的應用，一種可能的方案是使用傳統的雜湊函式——例如MD5，但是這種方案會對時間平移、CD讀取錯誤、不同的音訊壓縮演算法或者音量調整的實現機制等情況非常敏感。使用一些類似於MD5的方法有利於迅速找到那些嚴格相同（從音訊檔的二進制資料來看）的音訊檔，但是要找到全部相同（從音訊檔的內容來看）的音訊檔就需要使用其他更進階的演算法了。
那些並不緊隨IT工業潮流的人往往能反其道而行之，對於那些微小差異足夠強韌的雜湊函式確實存在。現存的絕大多數雜湊演算法都是不夠強韌的，但是有少數雜湊演算法能夠達到辨別從嘈雜房間裡的揚聲器里播放出來的音樂的強韌性。有一個實際的例子是Shazam[1] （頁面存檔備份，存於網際網路檔案館） 服務。使用者可以用手機打開其app，並將話筒靠近用於播放音樂的揚聲器。該項服務會分析正在播放的音樂，並將它於儲存在資料庫中的已知的雜湊值進行比較。使用者就能夠收到被辨識的音樂的曲名。
目前常見的雜湊演算法
| 演算法名稱 | 輸出大小(bits) | 內部大小 | 區塊大小 | 長度大小 | 字元尺寸 | 碰撞情形 |
|---|---|---|---|---|---|---|
| HAVAL | 256/224/192/160/128 | 256 | 1024 | 64 | 32 | 是 |
| MD2 | 128 | 384 | 128 | No | 8 | 大多數 |
| MD4 | 128 | 128 | 512 | 64 | 32 | 是 |
| MD5 | 128 | 128 | 512 | 64 | 32 | 是 |
| PANAMA | 256 | 8736 | 256 | 否 | 32 | 是 |
| RadioGatún | 任意長度 | 58字 | 3字 | 否 | 1-64 | 否 |
| RIPEMD | 128 | 128 | 512 | 64 | 32 | 是 |
| RIPEMD-128/256 | 128/256 | 128/256 | 512 | 64 | 32 | 否 |
| RIPEMD-160/320 | 160/320 | 160/320 | 512 | 64 | 32 | 否 |
| SHA-0 | 160 | 160 | 512 | 64 | 32 | 是 |
| SHA-1 | 160 | 160 | 512 | 64 | 32 | 有缺陷 |
| SHA-256/224 | 256/224 | 256 | 512 | 64 | 32 | 否 |
| SHA-512/384 | 512/384 | 512 | 1024 | 128 | 64 | 否 |
| Tiger（2）-192/160/128 | 192/160/128 | 192 | 512 | 64 | 64 | 否 |
| WHIRLPOOL | 512 | 512 | 512 | 256 | 8 | 否 |
Rabin-Karp字串搜尋演算法是一個相對快速的字串搜尋演算法，它所需要的平均搜尋時間是O(n)。這個演算法是建立在使用雜湊來比較字串的基礎上的。
參閱
參考文獻
外部連結
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
