截角十二面體

在幾何學中，截角十二面體是一種由正十邊形和正三角形組成的三十二面體^[1]，是一種阿基米德立體^[2]。其每個頂點都是1個三角形和2個十邊形的公共頂點，具有每個頂角相等的性質，因此截角十二面體是一種半正多面體^[3]。

截角十二面體

(按這裡觀看旋轉模型)
類別	半正多面體
對偶多面體	三角化二十面體
識別
名稱	截角十二面體
參考索引	U26, C29, W10
鮑爾斯縮寫 （verse-and-dimensions的wikia：Bowers acronym）	tid
數學表示法
考克斯特符號 （英語：Coxeter-Dynkin diagram）
施萊夫利符號	t{5,3}
威佐夫符號 （英語：Wythoff symbol）	2 3 | 5
康威表示法	tD
性質
面	32
邊	90
頂點	60
歐拉特徵數	F=32, E=90, V=60 （χ=2）
組成與佈局
面的種類	正三角形 正十邊形
面的佈局 （英語：Face configuration）	20個{3} 12個{10}
頂點圖	3.10.10
對稱性
對稱群	Ih群
特性
-
圖像
3.10.10 （頂點圖） 三角化二十面體 （對偶多面體） （展開圖）
閱 論 編

性質

截角十二面體共有32個面、90條邊和60個頂點^[4]，每個頂點都是1個三角形和2個十邊形的公共頂點，其頂點圖可以用3.10.10來表示，也可以簡寫為3.10^2[5]。

構造

截角十二面體可以經由正十二面體透過截角變換構造而成。截角變換使得正十二面體原本的正五邊形面變成正十邊形面，並在原本的頂點處形成正三角形。

體積與表面積

邊長為a的截角十二面體體積V和表面積A分別為：

${\displaystyle A=5\left({\sqrt {3}}+6{\sqrt {5+2{\sqrt {5}}}}\right)a^{2}\approx 100.990\,76a^{2}}$

${\displaystyle V={\frac {5}{12}}\left(99+47{\sqrt {5}}\right)a^{3}\approx 85.039\,6646a^{3}}$

頂點坐標

邊長為2φ − 2且幾何中心位於原點的截角十二面體^[6]其頂點坐標為^[7]：

${\displaystyle \left(0\,,\pm {\frac {1}{\varphi }}\,,\pm {\left({\begin{smallmatrix}2+\varphi \end{smallmatrix}}\right)}\right)}$、

${\displaystyle \left(\pm {\frac {1}{\varphi }}\,,\pm {\varphi }\,,\pm {2{\varphi }}\right)}$、

(±φ, ±2, ±(φ + 1))。

其中φ = ${\displaystyle {\frac {1+{\sqrt {5}}}{2}}}$，為黃金比例.

球面鑲嵌和施萊格爾圖

截角十二面體對應的結構也可以構建成球面鑲嵌，並以球極平面投影的方式呈現。

正投影圖（英語：Orthographic projection）	球極平面投影
	以十邊形為中心	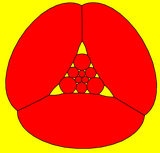以正三角形為中心
透視圖	施萊格爾圖

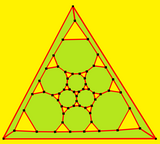
頂點佈局

有一些多面體與截角十二面體具有相同的頂點佈局（英語：Vertex_arrangement），換句話說，及他們與截角十二面體共用頂點、或者可以具有相同的頂點坐標。這些多面體有^[8][9][10]：

截角十二面體（原像）

大二十合二十合十二體（英語：Great icosicosidodecahedron）

大雙三角十二面截半二十面體

大十二合二十面體（英語：Great dodecicosahedron）

相關多面體及密鋪

截角二十面體是正二十面體經過截半變換後的結果，其他也是由正二十面體透過康威變換得到的多面體有：

正二十面體家族半正多面體

對稱群: [5,3]（英語：Icosahedral symmetry）, (*532)							[5,3]+, (532)
{5,3}	t0,1{5,3}	t1{5,3}	t0,1{3,5}	{3,5}	t0,2{5,3}	t0,1,2{5,3}	s{5,3}
半正多面體對偶
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

截角二十面體可以獨立填滿雙曲仿緊三維空間，這種由幾何結構稱為截角十二面體堆砌^[11]。

參見

• 正十二面體

參考文獻

1. Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
2. Cromwell, P. Polyhedra. United Kingdom: Cambridge. 1997: 79-86 Archimedean solids. ISBN 0-521-55432-2.

1. Weisstein, Eric W. (編). Truncated Dodecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
2. Cromwell, P. Polyhedra, CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids
3. Kasahara, K. "The Final Semiregular Polyhedron". Origami Omnibus: Paper-Folding for Everyone.. Tokyo: Japan Publications. 1988: p. 229. ISBN 978-4817090010. 引文格式1維護：冗餘文本 (link)
4. Geometry Technologies. "Truncated Dodecahedron.". scienceu. [2016-08-30]. （原始內容存檔於2016-08-06）.
5. Cundy, H. and Rollett, A. "Truncated Dodecahedron. 3.10²." §3.7.9 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 109, 1989. ISBN 978-0906212202
6. Weisstein, Eric W. (編). Icosahedral group. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
7. Archimedean Solids: Truncated Dodecahedron. dmccooey.com. （原始內容存檔於2016-03-12）.
8. Weisstein, Eric W. (編). 大二十合二十合十二體. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
9. Weisstein, Eric W. (編). 大二重三角十二面截半二十面體. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
10. Weisstein, Eric W. (編). 大十二合二十面體. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
11. N.W. Johnson（英語：Norman Johnson (mathematician)）: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

外部連結

• 埃里克·韋斯坦因, 截角十二面體 （參閱阿基米德立體） 於MathWorld（英文）
• Klitzing, Richard. 3D convex uniform polyhedra o3x5x - tid. bendwavy.org.
• Editable printable net of a truncated dodecahedron with interactive 3D view （頁面存檔備份，存於網際網路檔案館）
• The Uniform Polyhedra （頁面存檔備份，存於網際網路檔案館）
• Virtual Reality Polyhedra （頁面存檔備份，存於網際網路檔案館） The Encyclopedia of Polyhedra