婆羅摩笈多公式

歐氏平面幾何中，婆羅摩笈多公式是用以計算圓內接四邊形的面積的公式，以印度數學家婆羅摩笈多之名命名。一般四邊形的面積公式請見布雷特施奈德公式。

基本形式

婆羅摩笈多公式的最簡單易記的形式，是圓內接四邊形面積計算。若圓內接四邊形的四邊長為a, b, c, d，則其面積為：

${\displaystyle {\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$

其中s為半周長：

${\displaystyle s={\frac {a+b+c+d}{2}}}$

證明

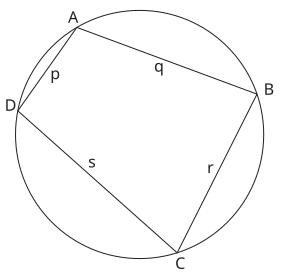
圓內接四邊形的面積 = ${\displaystyle \triangle ADB}$的面積 + ${\displaystyle \triangle BDC}$的面積

${\displaystyle ={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin C.}$

但由於${\displaystyle ABCD}$是圓內接四邊形，因此${\displaystyle \angle DAB=180^{\circ }-\angle DCB}$。故${\displaystyle \sin A=\sin C}$。所以：

${\displaystyle {\mbox{Area}}={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin A}$

${\displaystyle ({\mbox{Area}})^{2}={\frac {1}{4}}\sin ^{2}A(pq+rs)^{2}}$

${\displaystyle 4({\mbox{Area}})^{2}=(1-\cos ^{2}A)(pq+rs)^{2}\,}$

${\displaystyle 4({\mbox{Area}})^{2}=(pq+rs)^{2}-cos^{2}A(pq+rs)^{2}.\,}$

對${\displaystyle \triangle ADB}$和${\displaystyle \triangle BDC}$利用餘弦定理，我們有：

${\displaystyle DB^{2}=p^{2}+q^{2}-2pq\cos A=r^{2}+s^{2}-2rs\cos C.\,}$

代入${\displaystyle \cos C=-\cos A}$（這是由於${\displaystyle A}$和${\displaystyle C}$是互補角），並整理，得：

${\displaystyle 2\cos A(pq+rs)=p^{2}+q^{2}-r^{2}-s^{2}.\,}$

把這個等式代入面積的公式中，得：

${\displaystyle 4({\mbox{Area}})^{2}=(pq+rs)^{2}-{\frac {1}{4}}(p^{2}+q^{2}-r^{2}-s^{2})^{2}}$

${\displaystyle 16({\mbox{Area}})^{2}=4(pq+rs)^{2}-(p^{2}+q^{2}-r^{2}-s^{2})^{2},\,}$

它是${\displaystyle a^{2}-b^{2}}$的形式，因此可以寫成${\displaystyle (a+b)(a-b)}$的形式：

${\displaystyle (2(pq+rs)+p^{2}+q^{2}-r^{2}-s^{2})(2(pq+rs)-p^{2}-q^{2}+r^{2}+s^{2})\,}$

${\displaystyle =[(p+q)^{2}-(r-s)^{2}][(r+s)^{2}-(p-q)^{2}]\,}$

${\displaystyle =(p+q+r-s)(p+q+s-r)(p+r+s-q)(q+r+s-p).\,}$

引入${\displaystyle T={\frac {p+q+r+s}{2}}}$，

${\displaystyle 16({\mbox{Area}})^{2}=16(T-p)(T-q)(T-r)(T-s).\,}$

兩邊開平方，得：

${\displaystyle {\mbox{Area}}={\sqrt {(T-p)(T-q)(T-r)(T-s)}}.}$

證畢。

更特殊情況

若圓O的圓內接四邊形的四邊長為a, b, c, d，且外切於圓C，則其面積為：

${\displaystyle {\sqrt {abcd}}}$

證明

由於四邊形內接於圓O，所以：

${\displaystyle S={\sqrt {(p-a)(p-b)(p-c)(p-d)}}}$

其中p為半周長：

${\displaystyle p={\frac {a+b+c+d}{2}}}$

又因為四邊形外切圓C，所以：

${\displaystyle a+c=b+d}$

則：

${\displaystyle p-a={\frac {b+c+d-a}{2}}={\frac {a+c+c-a}{2}}=c}$

同理:

${\displaystyle p-b=d}$， ${\displaystyle p-c=a}$， ${\displaystyle p-d=b}$

綜上：

${\displaystyle S={\sqrt {abcd}}}$

證畢。

一般情況

布雷特施奈德公式

對一般四邊形的面積有布雷特施奈德公式，其敘述如下：

${\displaystyle {\sqrt {(p-a)(p-b)(p-c)(p-d)-abcd\cos ^{2}\theta }}}$

其中 ${\displaystyle \theta }$ 是四邊形一對對角和的一半。

注意到不論取到哪一對對角 ${\displaystyle \cos ^{2}\theta }$ 的值都一樣，因為四邊形的內角和是 ${\displaystyle 2\pi }$，故如果選取到的是另一對角，其對角和的一半是 ${\displaystyle \pi -\theta }$。而 ${\displaystyle \cos(\pi -\theta )=-\cos \,\theta }$，所以有 ${\displaystyle \cos ^{2}(\pi -\theta )=\cos ^{2}\theta }$。

假設此時四邊形恰好四頂點共圓，由於圓內接四邊形的對角和為 ${\displaystyle \pi }$，因此 ${\displaystyle \theta ={\pi \over 2}}$，而且由 ${\displaystyle \cos \,{\pi \over 2}=0}$，可推得此時 ${\displaystyle abcd\cos ^{2}\theta =0}$，布雷特施奈德公式恰好退化回婆羅摩笈多公式。

柯立芝公式

另一個由柯立芝所證明的公式如下^[1]：

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-\textstyle {1 \over 4}(ac+bd+pq)(ac+bd-pq)}}\,}$

其中 p 及 q 為四邊形對角線之長。在圓內接四邊形中，根據托勒密定理我們有${\displaystyle pq=ac+bd}$，此公式退化回為婆羅摩笈多公式。

相關定理

海倫公式給出三角形的面積。它是婆羅摩笈多公式取${\displaystyle d=0}$的特殊情形。

婆羅摩笈多公式的基本形式和擴充形式，就像由勾股定理擴充至餘弦定理一般。

1. J. L. Coolidge, "A Historically Interesting Formula for the Area of a Quadrilateral", American Mathematical Monthly, 46 (1939) pp. 345-347.