热门问题
时间线
聊天
视角
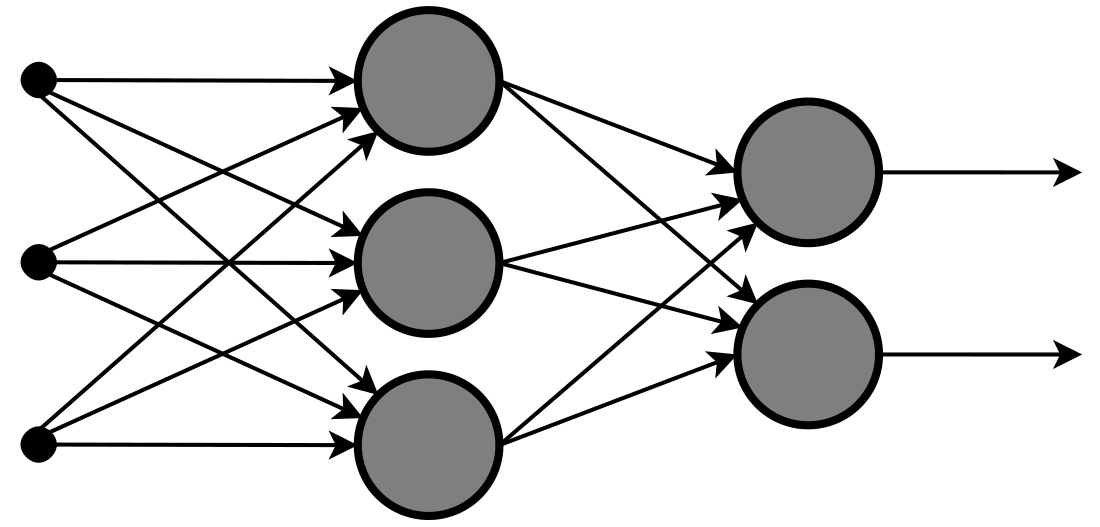
反向傳播演算法
人工神經網絡的優化算法 来自维基百科,自由的百科全书
Remove ads
反向傳播(英語:Backpropagation,意為誤差反向傳播,縮寫為BP)是對多層類神經網路進行梯度下降的演算法,也就是用鏈式法則以網路每層的權重為變數計算損失函式的梯度,以更新權重來最小化損失函式。
動機
任何監督式學習演算法的目標是找到一個能把一組輸入最好地對映到其正確的輸出的函式。例如一個簡單的分類任務,其中輸入是動物的圖像,正確的輸出將是動物的名稱。一些輸入和輸出模式可以很容易地通過單層神經網路(如感知器)學習。但是這些單層的感知機只能學習一些比較簡單的模式,例如那些非線性可分的模式。例如,人可以通過辨識動物的圖像的某些特徵進行分類,例如肢的數目,外觀的紋理(無論是毛皮,羽毛,鱗片等),該動物的體型,以及種種其他特徵。但是,單層神經網路必須僅僅使用圖像中的像素的強度來學習一個輸出一個標籤函式。因為它被限制為僅具有一個層,所以沒有辦法從輸入中學習到任何抽象特徵。多層的網路克服了這一限制,因為它可以建立內部表示,並在每一層學習不同的特徵。[1]第一層可能負責從圖像的單個像素的輸入學習線條的走向。第二層可能就會結合第一層所學並學習辨識簡單形狀(如圓形)。每升高一層就學習越來越多的抽象特徵,如上文提到的用來圖像分類。每一層都是從它下方的層中找到模式,就是這種能力建立了獨立於為多層網路提供能量的外界輸入的內部表達形式。 反向傳播演算法的發展的目標和動機是找到一種訓練的多層神經網路的方法,於是它可以學習合適的內部表達來讓它學習任意的輸入到輸出的對映。[1]
Remove ads
概括
反向傳播演算法(BP 演算法)主要由兩個階段組成:激勵傳播與權重更新。
每次迭代中的傳播環節包含兩步:
- (前向傳播階段)將訓練輸入送入網路以獲得預測結果;
- (反向傳播階段)對預測結果同訓練目標求差(損失函式)。
對於每個突觸上的權重,按照以下步驟進行更新:
- 將輸入激勵和回應誤差相乘,從而獲得權重的梯度;
- 將這個梯度乘上一個比例並取反後加到權重上。
這個比例(百分比)將會影響到訓練過程的速度和效果,因此成為「訓練因子」。梯度的方向指明了誤差擴大的方向,因此在更新權重的時候需要對其取反,從而減小權重引起的誤差。
第 1 和第 2 階段可以反覆迴圈迭代,直到網路對輸入的回應達到滿意的預定的目標範圍為止。
演算法
假設多層類神經網路的第 層是由線性算子 和啟用函式 所構成,也就是說,第 層的輸入是 維實數向量
輸出則為 維實向量
換句話說,第 層的輸出 就是第 層的輸入。
而 和 的具體(以第 分量表示)遞迴關係為
- ( )
上式通常會簡寫為
若這個多層類神經網路總共有 層,也就是說, 是最一開始的輸入,而 是最後一層的輸出,那跟損失函式 是以最後一層輸出 的各分量 (與真實值)為變數。依據上面的遞迴關係,可以把 進一步的轉成以第 層的輸入 與權重因子 為變數的函式
- ( , )
由此可以歸納到 的情況(注意到前幾層的權重因子不會消失在表達式中)
- ( , )
那這樣如果假設適當的可微分條件,由鏈式法則會有以下的遞迴關係 ( 若取 和 )
這樣就可以依據這個遞迴關係進行梯度下降,因為計算上是由 對 損失函式 的偏微分出發,一層層向後遞推出前面各層的權重因子梯度,所以被稱為反向傳播。
注意到可將輸入設為
並多加一行權重因子 為偏移,就可以把有偏移的多層網路納入剛剛討論的範圍內。
Remove ads
三層網路演算法(只有一個隱藏層):
初始化网络权值(通常是小的随机值)
do
forEach 训练样本 ex
prediction = neural-net-output(network, ex) // 正向传递
actual = teacher-output(ex)
计算输出单元的误差 (prediction - actual)
计算 对于所有隐藏层到输出层的权值 // 反向传递
计算 对于所有输入层到隐藏层的权值 // 继续反向传递
更新网络权值 // 输入层不会被误差估计改变
until 所有样本正确分类或满足其他停止标准
return 该网络
這個演算法的名稱意味著誤差會從輸出結點反向傳播到輸入結點。嚴格地講,反向傳播演算法對網路的可修改權值計算了網路誤差的梯度。[2]這個梯度會在簡單隨機梯度下降法中經常用來求最小化誤差的權重。通常「反向傳播」這個詞使用更一般的含義,用來指涵蓋了計算梯度以及在隨機梯度下降法中使用的整個過程。在適用反向傳播演算法的網路中,它通常可以快速收斂到令人滿意的極小值。
Remove ads
直觀理解
在給出反向傳播演算法的數學推導之前,我們舉一個例子來培養關於神經元的真實輸出與正確輸出間的直觀感受。考慮一個有兩個輸入單元、一個輸出單元、沒有隱藏單元的簡單神經網路。每個神經元都使用輸入的加權作為線性輸出[note 1]。

在訓練之前,我們將隨機分配權重。之後神經元根據訓練實例進行學習。在此例中,訓練集為 (, , ),其中 與 是網路的輸入, 為正確輸出(在給定相同的輸入時網路最終應當產生的輸出)。網路在給定 和 時,會計算一個輸出 ,很可能與 不同(因為權重最初是隨機的)。為了衡量期望輸出 與實際輸出 之間的差異,一個常用的方法是採用平方誤差測度:
- ,
其中 為誤差。
舉例來講,考慮單一訓練實例的網路:,輸入 與 均為1,正確輸出 為 0。現在若將實際輸出 畫在x軸,誤差 畫在 軸,得出的是一條拋物線。拋物線的極小值對應輸出 ,最小化了誤差 。對於單一訓練實例,極小值還會接觸到 軸,這意味著誤差為零,網路可以產生與期望輸出 完全匹配的輸出 。因此,把輸入對映到輸出的問題就化為了一個找到一個能產生最小誤差的函式的最佳化問題。

然而,一個神經元的輸出取決於其所有輸入的加權總和:
- ,
其中 和 是從輸入單元到輸出單元相連的權重。因此,誤差取決於輸入到該神經元的權重,也是網路要學習最終需要改變的。若每個權重都畫在一個水平的軸上,而誤差畫在垂直軸上,得出的就是一個拋物面(若一個神經元有 個權重,則誤差曲面的維度就會是 ,因而就是二維拋物線的 維等價)。

反向傳播演算法的目的是找到一組能最大限度地減小誤差的權重。尋找拋物線或任意維度中的任何函式的極大值的方法有若干種。其中一種方法是通過求解方程組,但這依賴於網路是一個線性系統,而目標也需要可以訓練多層非線性網路(因為多層線性網路與單層網路等價)。在反向傳播中使用的方法是梯度下降法。
Remove ads
梯度下降法背後的直觀感受可以用假設情境進行說明。一個被卡在山上的人正在試圖下山(即試圖找到極小值)。大霧使得能見度非常低。因此,下山的道路是看不見的,所以他必須利用局部資訊來找到極小值。他可以使用梯度下降法,該方法涉及到察看在他當前位置山的陡峭程度,然後沿著負陡度(即下坡)最大的方向前進。如果他要找到山頂(即極大值)的話,他需要沿著正陡度(即上坡)最大的方向前進。使用此方法,他會最終找到下山的路。不過,要假設山的陡度不能通過簡單地觀察得到,而需要複雜的工具測量,而這個工具此人恰好有。需要相當長的一段時間用儀器測量山的陡峭度,因此如果他想在日落之前下山,就需要最小化儀器的使用率。問題就在於怎樣選取他測量山的陡峭度的頻率才不致偏離路線。
在這個類比中,此人代表反向傳播演算法,而下山路徑表示能使誤差最小化的權重集合。山的陡度表示誤差曲面在該點的斜率。他要前行的方向對應於誤差曲面在該點的梯度。用來測量陡峭度的工具是微分(誤差曲面的斜率可以通過對平方誤差函式在該點求導數計算出來)。他在兩次測量之間前行的距離(與測量頻率成正比)是演算法的學習速率。參見限制一節中對此類型「爬山」演算法的限制的討論。
Remove ads
限制
歷史
弗拉基米爾·瓦普尼克在他的書《支持向量機》中首次發表反向傳播演算法。在1969年阿瑟·E·布萊森和何毓琦將其描述為多級動態系統最佳化方法。[5][6]直到1974年以後在神經網路的背景下應用,並由保羅·維波斯[7]、大衛·魯梅爾哈特、傑弗里·辛頓和羅納德·J·威廉斯[1][8]的著作,它才獲得認可,並引發了一場類神經網路的研究領域的「文藝復興」。在21世紀初人們對其失去興趣,但在2010年後又擁有了興趣,如今可以通過GPU等大型現代運算器件用於訓練更大的網路。例如在2013年,頂級語音辨識器現在使用反向傳播演算法訓練神經網路。
注釋
- 注意多層神經網路一般採用非線性的啟用功能,而此例中的啟用功能為線性函式,所以並不能給出明確的示範。雖然多層神經網路的誤差表面要複雜許多,但在小範圍內,我們可以用一個拋物面來估測這樣的複雜表面。我們在這裡採用線性的例子,因為它們簡單易懂。
參見
參考文獻
外部連結
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads











![{\displaystyle {y^{l}}_{i}=f^{l}\{\,[W^{l}(y^{l-1})]_{i}\,\}=f^{l}\left[\,\sum _{j=1}^{n_{l-1}}y_{j}^{l-1}W_{ji}^{l}\,\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/aba5eff2a6aa2182cd0d8d817cab7802260f989a)

![{\displaystyle y^{l}=f^{l}[\,W^{l}(y^{l-1})\,]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/dac7132bdbe0b82209526d961a1f3256496708bd)








![{\displaystyle g^{L}(W_{ij}^{L},\,{y_{k}^{L-1}})=g\left[\,f^{L}\left(\sum _{a=1}^{n_{L-1}}y_{a}^{L-1}W_{ab}^{L}\right)\,\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/709187afeb6e1ee568418c275ef37a95a93b7f2b)



![{\displaystyle g^{l}(W_{ij}^{l},\,\cdots ,\,W_{ij}^{L},\,{y_{k}^{l-1}})=g^{l+1}\left[\,W_{ij}^{l+1},\,\cdots ,\,W_{ij}^{L},\,f^{l}\left(\sum _{a=1}^{n_{l-1}}y_{a}^{l-1}W_{ab}^{l}\right)\,\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/533ab27b2cdca377c09cc1b8b45e6198d32d7910)





![{\displaystyle {\frac {\partial g^{l}}{\partial {y^{l-1}}_{c}}}=\sum _{i=1}^{n_{l}}\left[\,{\frac {\partial g^{l+1}}{\partial {y^{l}}_{i}}}{\bigg |}_{{y^{l}}_{i}=f^{l}(x)}\times {\frac {df^{l}}{dx}}{\bigg |}_{x=\sum {y^{l-1}}_{a}W_{ai}^{l}}\times W_{ci}^{l}\,\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/692b0e646ebca799aca9376725544fa6f30ac37e)


















