負回授放大器

負回授放大器（英語：negative feedback amplifier）是一種將輸出訊號按比例回授回輸入訊號，從而達到控制的放大器。通過引入負回授，放大器的性能，例如增益的穩定性、線性、頻率響應、階躍響應等，可以得到改善。此外，製造過程以及使用環境所造成的元件參數偏差對放大器性能的影響，可以通過引入負回授緩解。由於以上優點，負回授放大器在許多放大電路以及控制系統中有著廣泛的應用。^[1]

圖1：理想的負回授模式

一個負回授放大器具有負回授模式的三個基本元素（如圖1）：一個開迴路增益為A_OL的放大器、一個係數為β < 1的負回授網絡以及一個加減運算電路。上述三個元素只有放大器本身是必須的，在某些情況中，另外兩個元素可能被省略。例如，在電壓跟隨器中，回授網絡以及求和電路並不必需。

概述

普遍地說，所有的電子設備都提供了一定的功率增益（例如真空管、雙極性電晶體和場效電晶體），然而它們實際上大多屬於非線性元件。負回授可以通過降低增益來改善元件的線性。如果放大器沒有正確地設計為負回授，那麼放大器的工作會變得不穩定，其產生的結果是一些不希望看到的行為，例如振盪。可以利用貝爾實驗室的哈里·奈奎斯（Harry Nyquist）研究出的奈奎斯特穩定判據來研究回授放大器的穩定性。

回授放大器具有以下特點：^[2]

優點：

• 能根據需要增加或減少輸入阻抗（根據回授形式）
• 能根據需要增加或減少輸出阻抗（根據回授形式）
• 降低訊號失真（增加線性）
• 展寬頻寬
• 使增益對參數擾動的靈敏度降低
• 能夠控制放大器的階躍響應

缺點：

• 如果設計不周，可能會導致工作不穩定
• 放大器的實際增益降低
• 接入回授的放大器（也稱閉迴路放大器）的輸入、輸出阻抗與未接入回授的放大器（也稱開迴路放大器）的增益有關。

歷史

負回授放大器是由哈羅德·史蒂芬·布萊克（Harold Stephen Black）在他1927年8月2日前往貝爾實驗室途中發明的。^[3]布萊克當時正在努力研究降低電話通信中中繼放大器訊號失真的解決辦法。當時，布萊克在他購買的《紐約時報》的一處空白記錄下了他的靈感，^[4]即一個類似圖1的框圖，以及一些推導的方程。^[5]他隨後在1928年8月8日向美國專利局提交了他的發明，之後耗費了8年時間才正式發表了這一專利。後來，布萊克寫到：「導致如此嚴重的時間延遲的原因之一是這一概念與專利局的固有思維太過違背，以至於他們最初認為這套系統根本不可能工作。」^[6]

經典回授

降低增益

在下面的敘述中，接入回授網絡的放大器的閉迴路增益（closed-loop gain）A_fb由放大器的開迴路增益（open-loop gain）A_OL以及回授係數β（決定輸出量以何種比例回授到輸入端）共同決定。如圖1，開迴路增益A_OL大多數情況下是頻率和電壓的函數；回授係數β由引入放大器的回授網絡形式決定。對於一個運算放大器，可以利用兩個電阻構成分壓器來為回授網絡設置介於0與1之間的回授係數。也可以引入電容器和電感元件等具有特殊響應特性的元件來修改回授網絡的特性，使其來實現調頻或者產生震盪特殊功能能夠。引入回授之後，電壓放大器的增益可以由下面的過程推導。

當沒有引入回授時，輸入電壓V'_in直接接在放大器的輸入端，相應的輸出電壓是

${\displaystyle V_{out}=A_{OL}\cdot V'_{in}}$

現在假設接入一個回授係數為β的回授電路，那麼，輸出電壓與輸入電壓與回授電壓的差值直接相關。這個差值作為接在放大器輸入端的「輸入電壓」

${\displaystyle V'_{in}=V_{in}-\beta \cdot V_{out}}$

將它代入第一個式中替換V'_in，則

${\displaystyle V_{out}=A_{OL}(V_{in}-\beta \cdot V_{out})}$

整理得

${\displaystyle V_{out}(1+\beta \cdot A_{OL})=V_{in}\cdot A_{OL}}$

這樣，回授放大器的閉迴路增益A_fb可以表達為

${\displaystyle A_{\mathrm {fb} }={\frac {V_{\mathrm {out} }}{V_{\mathrm {in} }}}={\frac {A_{OL}}{1+\beta \cdot A_{OL}}}}$

如果A_OL >> 1，那麼A_fb ≈ 1 / β，並且等效的放大倍數（閉迴路增益）A_fb，則可以通過改變回授係數β來設置，由此改變回授網絡的性能（這樣的回授系統通常可以方便地設置），提高放大的線性以及穩定性。同時需要注意的是，如果β A_OL = −1，則放大器的實際增益為無窮大，這樣放大器將產生振盪，系統將變得不穩定。二者的乘積可以在奈奎斯特圖中顯示整個回授網絡的穩定性（也可以利用更為簡單的波德圖進行分析）。

L = β A_OL在回授分析中十分常見，有時也被稱作是環路增益（loop gain）。(1 + β A_OL)在分析中也較為常見，被稱為倒靈敏度因數（desensitivity factor）或改善因數（improvement factor）。

展寬頻寬

圖2：具有回授和不具有回授的單級放大器的增益-頻率曲線；截止頻率在圖中被標識出。

回授網絡也可以被用來展寬放大器的頻寬，但是增益相應地必須減少。^[7]圖2展示了上述的這一點，可以通過下面的方式理解此曲線圖：當沒有介入回授網絡，開迴路增益中只含有一個頻率響應時間常數

${\displaystyle A_{OL}(f)={\frac {A_{0}}{1+jf/f_{C}}}\ ,}$

這裡，f_C為放大器的截止頻率。在這一例子中，f_C = 10⁴赫茲，零位頻率時的增益為A₀ = 10⁵。上圖顯示了截止頻率左側，增益基本維持不變，不過當頻率大於截止頻率，增益會下降。當回授網絡被引入，則閉迴路增益的計算公式為

${\displaystyle A_{fb}(f)={\frac {A_{OL}}{1+\beta A_{OL}}}}$

${\displaystyle ={\frac {A_{0}/(1+jf/f_{C})}{1+\beta A_{0}/(1+jf/f_{C})}}}$

${\displaystyle ={\frac {A_{0}}{1+jf/f_{C}+\beta A_{0}}}}$

${\displaystyle ={\frac {A_{0}}{(1+\beta A_{0})\left(1+j{\frac {f}{(1+\beta A_{0})f_{C}}}\right)}}\ .}$

上面最後一式表示，回授放大器仍然具有單一時間常數的行為方式，但是截止頻率通過乘以(1 + β A₀)得到了擴展，不過零位頻率處的增益幾乎以相同的倍數減少。這一特性被稱作是增益帶交換（gain-bandwidth tradeoff）。增益和帶寬總是此消彼長。在圖2中，(1 + β A₀) = 10³，因此A_fb(0) = 10⁵ / 10³ = 100 V/V，f_C增加到10⁴×10³ = 10⁷赫茲。

當放大器的開迴路增益具有多個極點，而非上述例子中所示的單極點，則引入回授可以得到復極點（complex poles，具有實部和虛部兩部分）。在雙極點的情況中，回授放大器在其截止頻率附近得到其最佳的頻率響應，且在階躍響應中會發生訊號過沖。當有多個極點時，回授放大器會變得不穩定，並產生振盪。對於複雜情況較為詳細的討論，可以參閱相關專業的文獻。^[8]

訊號流分析

上述的說明有一個理想化的處理，就是將網絡分割成兩個獨立的模塊（即擁有各自獨立確定的傳遞函數），這是「電路劃分」的一個例子，^[9]在此情況下就是指劃分為一個順向放大模塊和一個回授模塊。在實際的放大器中，信息流不是像這裡展示的如此單向化。^[10]通常這些模塊會視為二埠網絡，考慮雙向的信息傳遞。^[11][12]然而，把放大器轉換成這種形式並不容易，尤其是當涉及到的回授並不是全局的（即直接從輸出到輸入）而是局部的（即回授網絡內涉及輸入或輸出端子以外的節點）。^[13][14]

以關於兩個內部變量x_j=Px_i的控制變量P為基礎的負回授放大電路的一種可能的訊號流圖。據D.Amico et al.繪圖^[15]

在這些更一般的情況下，放大器的分析更為直接，不用像圖中劃分成模塊，而是使用基於訊號流分析的分析，如回歸比法（英語：Return ratio）以及漸近增益模型。^[16][17][18] Choma對訊號流的方法評論道：^[19]

"In contrast to block diagram and two-port approaches to the feedback network analysis problem, signal flow methods mandate no a priori assumptions as to the unilateral or bilateral properties of the open loop and feedback subcircuits. Moreover, they are not predicated on mutually independent open loop and feedback subcircuit transfer functions, and they do not require that feedback be implemented only globally. Indeed signal flow techniques do not even require explicit identification of the open loop and feedback subcircuits. Signal flow thus removes the detriments pervasive of conventional feedback network analyses but additionally, it proves to be computationally efficient as well."

採用此建議，根據D'Amico et al.作出一個負回授放大器的訊號流圖。^[15]根據這些作者的用法，記號如下：

"變量x_S, x_O表示輸入和輸出訊號，此外準確示出了，其他兩個變量x_i, x_j通過控制變量P聯繫起來。變量a_ij為權重分支。變量x_i, x_j和控制變量P類比了一個受控的發電機，或者說是電路兩個結點間電壓和電流的關係。

右圖中，記 a₁₁為控制變量P置零後輸入和輸出的傳遞函數；a₁₂為輸入源x_S指令後輸出和受控變量x_j之間的傳遞函數；a₂₁表示受控變量x_j置零（即控制參數P置零）後源變量和內部變量之間的傳遞函數；a₂₂給出控制變量P和輸入變量x_S均置零後獨立內部變量和受控內部變量的關係。"

運用此圖，這些作者推導出用控制變量P表示的一般性的增益表達式，定義了受控源關係x_j=P x_i:

${\displaystyle x_{O}=a_{11}x_{S}+a_{12}x_{j}\ ,}$

${\displaystyle x_{i}=a_{21}x_{S}+a_{22}x_{j}\ ,}$

和

${\displaystyle x_{j}=Px_{i}\ .}$

結合這些結果，增益就為：

${\displaystyle {\frac {x_{O}}{x_{S}}}=a_{11}+{\frac {a_{12}a_{21}P}{1-Pa_{22}}}\ .}$

運用這個公式，需要找出特定放大電路的關鍵受控源。例如，P可以是如D'Amico et al.中特定情形的一個二埠網絡的控制變量。^[15]再舉一個不同的例子，如果令a₁₂=a₁₂=1, P=A, a₂₂= –β（負回授）以及a₁₁=0（無正回授），我們重新得到了簡單的兩個單向模塊的結果。

用二埠網絡分析回授

用二埠分析負回授放大器的各種拓撲結構。左上：電流放大器；右上：互導；左下：互阻；右下：電壓放大器。^[20]

儘管訊號流分析一節中提到的一些訊號流分析的形式是處理負回授放大器最一般的形式，表示成兩個二埠卻是教科書中最常見的方法，並在這裡給出。它保持了放大器的兩模塊的電路分割，但允許雙向的模塊。此方法的一些缺陷將在結尾處闡述。

放大器使用電壓或者電流作為其輸入訊號以及輸出訊號，因此總共有4種回授接法。所有接法都是利用最簡單的開迴路放大器引入回授網絡。不同的接法的設計目標有所不同，其類型不一定與開迴路放大器的類型相同。例如，一個運算放大器（電壓放大）可以通過其他的接法來充當電流放大的功能。

任何類型的負回授放大器都可使用二埠網絡的組合來實現。有四種二埠網絡，如何選擇取決於回授的類型，圖中展示了這4種不同的連接拓撲結構。這些接法通常稱為串聯接法或並聯接法。^[21][22]圖中左面一欄是並聯輸入；右面一欄是串聯輸入。上面一行是串聯輸出；下面一行是並聯輸出。連接和雙埠的各種組合見下表。

回授放大器類型	輸入連接	輸出連接	理想回授網絡	兩埠回授
電流	並聯	串聯	CCCS	g參數
互阻	並聯	並聯	CCVS	y參數
互導	串聯	串聯	VCCS	z參數
電壓	串聯	並聯	VCVS	h參數

比如，對於一個電流回授放大器，輸出電流被取樣，並與輸入電流合併。於是，理想情況下的回授是使用（輸出）電流控制電流源（CCCS）工作的，使用二埠網絡的不完美實現也必須包含一個CCCS，也就是說，回授網絡應當選擇g參數二埠網絡。這裡使用漸進增益模型（英語：asymptotic gain model）一文中處理的電路來給出大多數教材中使用的兩埠的方法。^[23][24][25]

圖3：電流並聯回授放大器

圖3中雙晶體放大器的有一回授電阻R_f。分析此電路的目的是求三個項目：增益、從負載端看過去的輸出阻抗、以及從輸入源看過去的輸入阻抗。

用二埠替代回授網絡

第一步是用二埠來替代回授網絡。那麼哪些部分要用二埠替代呢？

在二埠的輸入端有R_f。如果R_f右側的電壓變化，就會改變R_f內的電流，這個電流要從流入電晶體基極的電流中減掉。也就是說，二埠的輸入端是一個由電阻R₂上端的電壓控制的受控電流源。

有人可能會說，放大器的第二級只是一個電壓跟隨器，將輸入電晶體集極上的電壓傳遞到R₂的上端。也就是說檢測到的輸出端的訊號就是輸入電晶體的集極電壓。這一觀點是合理的，但是電壓跟隨器一級成為了回授網絡的一部分，從而使得分析回授更加複雜了。

圖4：g參數回授網絡

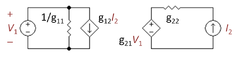
另一種觀點是，R₂上端的電壓是由輸出電晶體的射極電流所確定的。這種觀點產生了一種由R₂與R_f組成的完全無源的回授網絡。因為回授的控制變量是發射級電流，所以回授是電流控制的電流源（CCCS）。如圖4所示，我們在4種二埠網絡中進行尋找，發現只有一個有CCCS是g參數的二埠。下一個任務是是選出g參數，使得圖四中的二埠與R₂和R_f組成的L型部分是等效的。這個選擇是一個大多僅需要觀察兩種分立情況的代數過程：一種是在V₁ = 0的情況下，使得二埠右側的VCVS短路；另一種是在I₂ = 0的情況下，使得左側的CCCS開路。這兩種情況下的代數計算比較簡單，比立刻解出所有變量容易的多。g參數的選取可以使得二埠與L型部分的作用方式相同，如下表格所示：

g11	g12	g21	g22
${\displaystyle {\frac {1}{R_{f}+R_{2}}}}$	${\displaystyle -{\frac {R_{2}}{R_{2}+R_{f}}}}$	${\displaystyle {\frac {R_{2}}{R_{2}+R_{f}}}}$	${\displaystyle R_{2}//R_{f}\ }$

圖5：用二埠作為回授網絡的小訊號電路；上面的陰影框：主放大器；下面的陰影框：回授二埠替代的R_f和R₂組成的L型部分。

小訊號電路

下一步就是用電晶體的混合π模型（英語：Hybrid-pi model）在原來位置畫出這個放大器的小訊號示意圖。圖5示意圖中的符號R₃ = R_C2 // R_L而R₁₁ = 1 / g₁₁，R₂₂ = g₂₂。

有負載的開迴路增益

圖3顯示的是輸出結點，而不是輸出變量的選取。可以選取將放大器的短路輸出電流（產生短路電流增益）。因為這個變量能很容易導出其他選取（例如，負載電壓或負載電流）的結果。下面就來求解短路電流增益。

首先求出有負載的開迴路增益。可通過令g₁₂ = g₂₁ = 0切斷回授。這樣做是為了找到在回授關閉時，由於電阻在回授網絡中而造成的放大器的增益的改變量。因為R₁₁, R_B，和r_π1都是並聯的，並且v₁ = v_π，所以計算是相當容易的。令R₁ = R₁₁ // R_B // r_π1。此外，i₂ = -(β+1)i_B。開迴路電流增益A_OL即為：

${\displaystyle A_{OL}={\frac {\beta i_{B}}{i_{S}}}=g_{m}R_{C}\left({\frac {\beta }{\beta +1}}\right)\left({\frac {R_{1}}{R_{22}+{\frac {r_{\pi 2}+R_{C}}{\beta +1}}}}\right)\ .}$

回授增益

在研究回授的經典方法中，VCVS代表的前饋（即g₂₁ v₁）被忽略。^[26]這使得圖5中的電路與圖1中的框圖類似，得到回授增益如下：

${\displaystyle A_{FB}={\frac {A_{OL}}{1+{\beta }_{FB}A_{OL}}}}$

${\displaystyle A_{FB}={\frac {A_{OL}}{1+{\frac {R_{2}}{R_{2}+R_{f}}}A_{OL}}}\ ,}$

在回授中，係數β_FB = −g₁₂。引入符號β_FB來標記回授係數，以區別於電晶體β係數。

輸入和輸出電阻

圖6：Circuit set-up for finding feedback amplifier input resistance

回授用來更好地匹配訊號源與負載。例如，一種直接耦合電壓源與電阻性負載可能會由於分壓導致訊號缺損，但是插入一個負回授放大器能夠增強由源可見的表 面負載，並減少表面驅動阻抗的負載，避免由於電壓分壓大而導致的訊號衰減。這種優勢並不局限於電壓放大器，並且類似的匹配改進可以應用在電流放大器，跨導放大器和跨阻放大器中。

為了解釋這些回授對阻抗的影響，首先對二埠理論與電阻定義的銜接進行補充說明，這樣它在放大器中的應用就比較容易了。

電阻定義的背景

圖6顯示了電壓回授放大器（左端）輸入電阻等效電路，與電流回授放大器（右端）等效電路。這些布局是密勒定理的典型運用。在電壓放大器的情況下，回授網絡的輸出電壓 βV_out是應用於串聯並且與輸入電壓V_x極性相反，V_x是從環路上流經的（但是但相對於地面，極性相同）。因此，放大器的輸入電阻R_in上有效降落的電壓與流經的電流都減小，以致電路輸入電阻增強（有人可能會說R_in明顯增加）。它的新值可以通過應用密勒定理計算（電壓）或電路的基本定律計算。因此基爾霍夫電壓定律提供：

${\displaystyle V_{x}=I_{x}R_{in}+\beta v_{out}\ ,}$

其中v_out = A_v v_in = A_v I_x R_in。

將上述方程的結果進行替代，求解含回授放大器的輸入電阻：

${\displaystyle R_{in}(fb)={\frac {V_{x}}{I_{x}}}=\left(1+\beta A_{v}\right)R_{in}\ .}$

參考文獻及注釋

1. Kuo, Benjamin C & Farid Golnaraghi. Automatic control systems Eighth edition. NY: Wiley. 2003: 46. ISBN 0471134767. 引文格式1維護：冗餘文本 (link)
2. Palumbo, Gaetano & Salvatore Pennisi. Feedback amplifiers: theory and design. Boston/Dordrecht/London: Kluwer Academic. 2002: 64. ISBN 0792376439.
3. . (PDF). [2005-10-24]. （原始內容 (PDF)存檔於2007-09-28）.
4. Currently on display at Bell Laboratories in Mountainside, New Jersey
5. Waldhauer, Fred. Feedback. NY: Wiley. 1982: 3. ISBN 0471053198.
6. Black, Harold. Inventing the negative feedback amplifier. IEEE Spectrum. Dec 1977.
7. RW Brodersen Analog circuit design: lectures on stability (PDF). [2012-01-15]. （原始內容存檔 (PDF)於2008-02-29）.
8. Willy M. C. Sansen. Analog design essentials. New York; Berlin: Springer. 2006: §0513–§0533, p. 155–165 [2012-01-16]. ISBN 0-387-25746-2. （原始內容存檔於2009-05-30）.
9. Partha Pratim Sahu. §8.2 Partitioning. VLSI Design. McGraw Hill Education. 2013: 253 [2015-02-06]. ISBN 9781259029844. （原始內容存檔於2020-08-02）. dividing a circuit into smaller parts ...[so]...the number of connections between parts is minimized
10. Gaetano Palumbo, Salvatore Pennisi. Feedback Amplifiers: Theory and Design. Springer Science & Business Media. 2002 [2015-02-06]. ISBN 9780792376439. （原始內容存檔於2020-08-02）. In real cases, unfortunately, blocks...cannot be assumed to be unidirectional.
11. Wai-Kai Chen. §1.2 Methods of analysis. Feedback, Nonlinear, and Distributed Circuits. CRC Press. 2009: 1-3 [2015-02-06]. ISBN 9781420058826. （原始內容存檔於2020-08-02）.
12. Donald O. Pederson, Kartikeya Mayaram. §5.2 Feedback for a general amplifier. Analog Integrated Circuits for Communication: Principles, Simulation and Design. Springer Science & Business Media. 2007: 105 ff [2015-02-06]. ISBN 9780387680309. （原始內容存檔於2020-08-02）.
13. Scott K Burgess & John Choma, Jr. §6.3 Circuit partitioning (PDF). Generalized feedback circuit analysis. [2015-02-06]. （原始內容 (PDF)存檔於2014-12-30）.
14. Gaetano Palumbo & Salvatore Pennisi. Feedback amplifiers: theory and design. Springer Science & Business Media. 2002: 66 [2015-02-06]. ISBN 9780792376439. （原始內容存檔於2020-08-02）.
15. Arnaldo D』Amico, Christian Falconi, Gianluca Giustolisi, Gaetano Palumbo. Resistance of Feedback Amplifiers: A novel representation (PDF). IEEE Trans Circuits & Systems - II Express Briefs. April 2007, 54 (4): 298 ff [2015-02-08]. （原始內容存檔 (PDF)於2020-08-02）.
16. For an introduction, see Rahul Sarpeshkar. Chapter 10: Return ratio analysis. Ultra Low Power Bioelectronics: Fundamentals, Biomedical Applications, and Bio-Inspired Systems. Cambridge University Press. 2010: 240 ff. ISBN 9781139485234.
17. Wai-Kai Chen. §11.2 Methods of analysis. Circuit Analysis and Feedback Amplifier Theory. CRC Press. 2005: 11–2 ff [2015-02-06]. ISBN 9781420037272. （原始內容存檔於2020-08-02）.
18. Gaetano Palumbo, Salvatore Pennisi. §3.3 The Rosenstark Method and §3.4 The Choma Method. Feedback Amplifiers: Theory and Design. Springer Science & Business Media. 2002: 69 ff. ISBN 9780792376439.
19. J Choma, Jr. Signal flow analysis of feedback networks. IEEE Trans Circuits & Systems. April 1990, 37 (4): 455–463 [2015-02-06]. doi:10.1109/31.52748. （原始內容存檔於2019-09-29）.
20. Richard C Jaeger. Figure 18.2. Microelectronic circuit design International. McGraw-Hill. 1997: 986 [2015-02-08]. （原始內容存檔於2020-08-02）.
21. Ashok K. Goel Feedback topologies (PDF). [2012-01-15]. （原始內容存檔 (PDF)於2008-02-29）.
22. Zimmer T & Geoffroy D: Feedback amplifier. [2013-04-28]. （原始內容存檔於2013-07-02）.
23. Vivek Subramanian: Lectures on feedback (PDF). [2015-02-10]. （原始內容存檔 (PDF)於2008-02-29）.
24. P R Gray, P J Hurst, S H Lewis, and R G Meyer. Analysis and Design of Analog Integrated Circuits Fourth Edition. New York: Wiley. 2001: 586–587 [2015-02-10]. ISBN 0-471-32168-0. （原始內容存檔於2009-02-19）. 引文格式1維護：冗餘文本 (link)
25. A. S. Sedra and K.C. Smith. Microelectronic Circuits Fifth Edition. New York: Oxford. 2004. Example 8.4, pp. 825–829 and PSpice simulation pp. 855–859 [2015-02-10]. ISBN 0-19-514251-9. （原始內容存檔於2009-02-04）. 引文格式1維護：冗餘文本 (link)
26. 如果考慮前饋的話，它會使開迴路增益發生變化，通常來說這個量相對於開迴路增益本身是相當小的，所以可以捨棄。還要注意到主放大器模塊是單向的。