安定时间

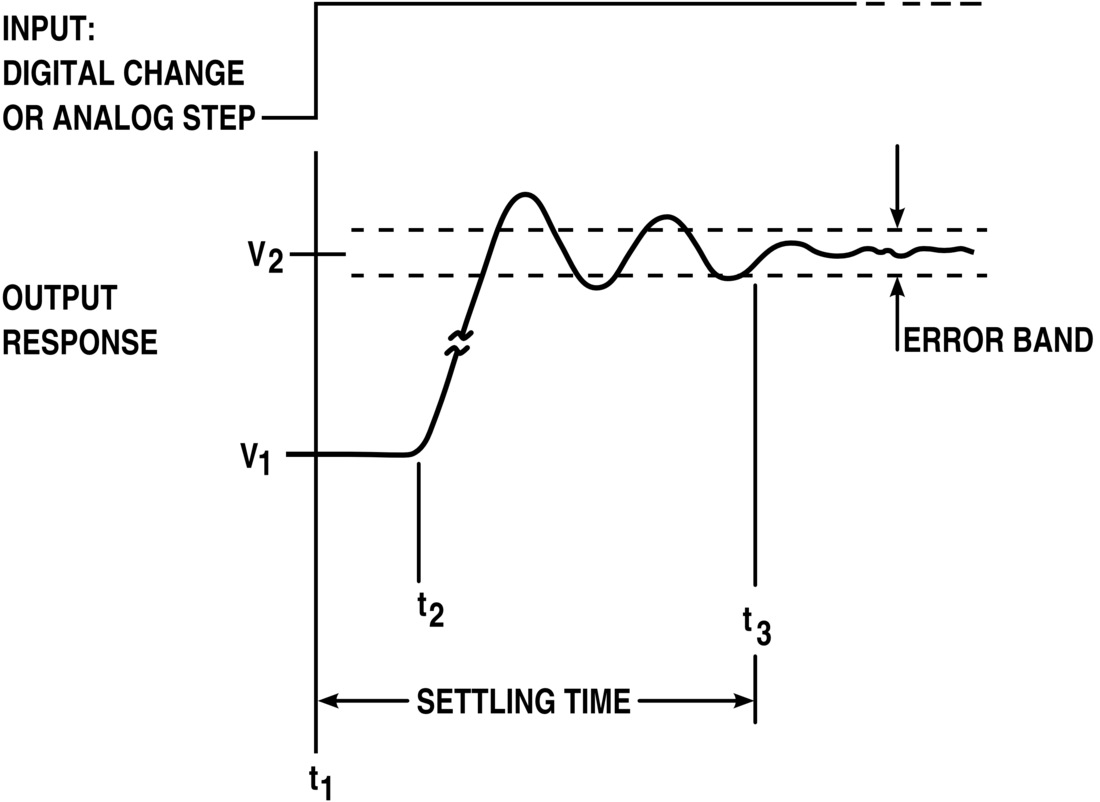
安定时间（Settling time）也称为整定时间，是指放大器或控制系统在步阶输入后，输出到达最终值，且其误差可维持在一定范围（一般是会对称于最终值）内的时间，是暂态响应的特性之一。安定时间包括很短的传播延迟，加上输出依照瞬态率（英语：Slew rate）振荡到最终值附近的时间，以及最后安定在允许误差附近的时间。

安定时间是在步阶输入后，输出到达最终值，且误差可维持在一定范围内的时间

有能量储存的系统无法立即反应，当输入变化或有扰动时会有暂态的现象^[1]。

定义

Tay, Mareels and Moore（1997）定义安定时间为“输出到达最终值附近，且和最终值之间的误差维持在一定范围（一般是5%到2%）内所需要的时间。”^[2]

数学细节

安定时间和系统响应及时间常数有关。

一阶系统

一阶RC电路的阶跃响应，三倍时间常数时输出到达输入的95%，在五倍时间常数时输出到达输入的99.3%

一阶系统较少定义安定时间，但一阶系统在三倍时间常数后，其输出和稳态的误差降至${\displaystyle e^{-3}\approx 0.05}$，五倍时间常数后，其输出和稳态的误差降至${\displaystyle e^{-5}\approx 0.0067}$^[3]，一般已可以忽略其误差^[4]。

二阶系统

若二阶欠阻尼系统的阻尼比${\displaystyle \zeta \ll 1}$，其步阶响应下的安定时间可以用以下式来近似：

${\displaystyle T_{s}=-{\frac {\ln({\text{tolerance fraction}})}{{\text{damping ratio}}\times {\text{natural freq}}}}}$

因此，误差在2%内的安定时间为：

${\displaystyle T_{s}=-{\frac {\ln(0.02)}{\zeta \omega _{n}}}\approx {\frac {4}{\zeta \omega _{n}}}}$^[5]

参考资料

1. Modern Control Engineering (5th Edition), Katsuhiko Ogata
2. Tay, Teng-Tiow; Iven Mareels; John B. Moore. High performance control. Birkhäuser. 1997: 93. ISBN 0-8176-4004-5.
3. 电工技术. 清华大学出版社有限公司. 2001: 98–. ISBN 978-7-302-04927-2.
4. 電路學(上). 五南图书出版股份有限公司. : 251–. ISBN 978-957-11-4162-6.
5. Richard C. Dorf; Robert H. Bishop. Modern Control Systems. Addison Wesley. 1995: 223. ISBN 0-201-50174-0. 引文使用过时参数coauthors (帮助)

相关条目

• 上升时间
• 步阶响应
• 时间常数

外部链接

• Second-Order System Example
• Op Amp Settling Time （页面存档备份，存于互联网档案馆）
• Graphical tutorial of Settling time and Risetime
• MATLAB function （页面存档备份，存于互联网档案馆） for computing settling time, rise time, and other step response characteristics