电磁波 (英文:Electromagnetic wave)是指同相 振荡 且互相垂直的电场 与磁场 ,是一种非机械波 ,在空间中以波 的形式传递能量 和动量 ,其传播方向垂直于电场与磁场的振荡方向。
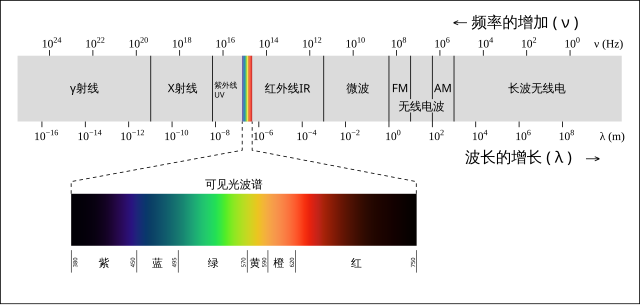
可见光谱只占有宽广的电磁波谱 的一小部分。 电磁波不需要依靠介质 进行传播,在真空 中其传播速度为光速 。电磁波可按照频率 分类,从低频率到高频率,主要包括无线电波 、兆赫辐射 、微波 、红外线 、可见光 、紫外线 、X射线 和伽马射线 。人眼可接收到的电磁波,波长 大约在380至780nm 之间,称为可见光。
詹姆斯·麦克斯韦 在可见光波长以外的电磁辐射被发现于19世纪初期。红外线 辐射的发现归因于天文学家威廉·赫歇尔 ,他于1800年在伦敦皇家学会 发表了他的成果。[ 1]
电磁波首先由詹姆斯·麦克斯韦 于1865年预测出来,而后由德国 物理学家海因里希·赫兹 于1887年至1888年间在实验中证实存在。[ 2] [ 3] 电磁波方程 ,一种波动方程 ,这清楚地显示出电场和磁场的波动本质。因为电磁波方程预测的电磁波速度与光速 的测量值相等,麦克斯韦推论光波 也是电磁波[ 4] [ 5] :283 。无线电波被海因里希·赫兹 在1887年第一个刻意产生,使用电路计算出比可见光低得多的频率上产生振荡,随之产生了由麦克斯韦方程所建议的振荡电荷和电流。赫兹还开发检测这些电波的方法,并产生和特征化这些后来被称为无线电波 和微波 。[ 6] :286,7
威廉·伦琴 发现并命名了X射线 。 在1895年11月8日的应用于真空管上的高电压试验后,他注意到在附近的镀膜玻璃板的荧光。在一个月内,他发现了X射线的主要性质。[ 6] :307
三种不同的电磁波波模 (mode )(蓝、绿、红),x-轴长度尺度是微米 。 电动力学 专门研究电磁波的物理行为,是电磁学 的分支。在电动力学里,根据麦克斯韦方程组 ,随着时间变化的电场产生了磁场,反之亦然。因此,一个振荡中的电场会产生振荡的磁场,而一个振荡中的磁场又会产生振荡的电场,这样子,这些连续不断同相振荡的电场和磁场共同地形成了电磁波[ 7] :326 [ 8] :894-897 。
电场,磁场都遵守叠加原理 。[ 9] :9 因为电场和磁场都是矢量场 ,所有的电场矢量和磁场矢量都适合做矢量加 运算。例如,一个行进电磁波 ,入射于一个介质,会引起介质内的电子振荡,因而使得它们自己也发射电磁波,因而造成折射 或衍射 等等现象[ 8] :959-968 。
在非线性介质内(例如,某些晶体 ),电磁波会与电场 或磁场 产生相互作用,这包括法拉第效应 [ 10] :366-368 、克尔效应 等等[ 11]
当电磁波从一种介质入射于另一种介质时,假若两种介质的折射率 不相等,则会产生折射 现象,电磁波的方向和速度会改变。斯涅尔定律 专门描述折射的物理行为[ 7] :388 。
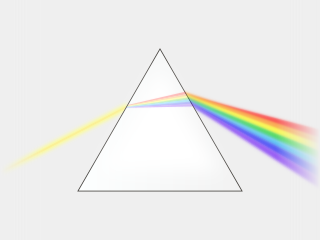
光通过三棱镜 后,因色散造成不同颜色折射 至不同的角度,让白光形成可见光谱 。 假设,由很多不同频率 的电磁波组成的光波,从空气入射于棱镜 。而因为菱镜内的材料的折射率跟电磁波的频率有关,会产生色散 现象:光波会色散成一组可观察到的电磁波谱 [ 7] :398-405 。
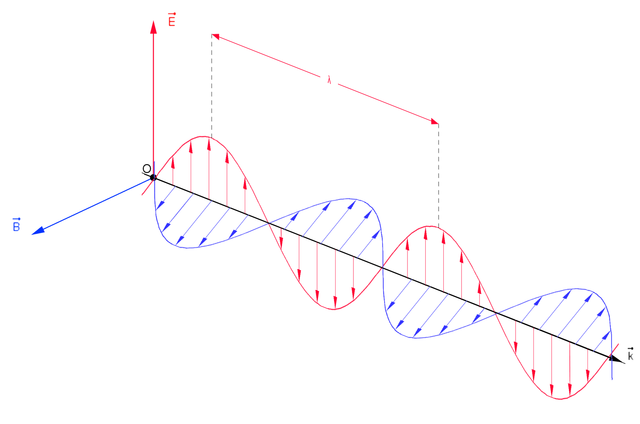
电磁波是横波,电场方向与磁场方向相互垂直,又都垂直于传播方向。 波是由很多前后相继的波峰 和波谷 所组成,两个相邻的波峰或波谷之间的距离称为波长 。电磁波的波长有很多不同的尺寸,从非常长的无线电波(有一个足球场那么长)到非常短的伽马射线(比原子半径还短)[ 8] :890 。
描述光波的一个很重要的物理参数是频率 。一个波的频率是它的振荡率,国际单位制 单位是赫兹 。每秒钟振荡一次的频率是一赫兹。频率与波长成反比:
v
=
ν
λ
{\displaystyle v=\nu \lambda \,\!}
其中,
v
{\displaystyle v\,\!}
ν
{\displaystyle \nu \,\!}
λ
{\displaystyle \lambda \,\!}
当波从一个介质传播至另一个介质时,波速会改变,但是频率不变[ 8] :961 。
干涉 是两个或两个以上的波,叠加形成新的波样式。假若这几个电磁波的电场同方向,磁场也同方向,则这干涉是相长干涉;反之,则是摧毁性干涉[ 8] :959-962 。
电磁波的能量,又称为辐射能 。这能量,一半储存于电场,另一半储存于磁场。用方程表达[ 8] :897-899 :
u
=
1
2
μ
0
B
2
+
ϵ
0
2
E
2
{\displaystyle u={\frac {1}{2\mu _{0}}}B^{2}+{\frac {\epsilon _{0}}{2}}E^{2}\,\!}
其中,
u
{\displaystyle u\,\!}
E
{\displaystyle E\,\!}
B
{\displaystyle B\,\!}
ϵ
0
{\displaystyle \epsilon _{0}\,\!}
电常数 ,
μ
0
{\displaystyle \mu _{0}\,\!}
磁常数 。
呈加速运动的电荷或随着时间而变化的电磁场,会产生电磁波。在自由空间里,电磁波以光速传播。准确的计算其物理行为必须引用推迟时间 的概念。这会增加电场和磁场的表达式的复杂程度(参阅杰斐缅柯方程 )。这些多加的项目详细地描述电磁波的物理行为。当任意一根导线(或别种导电体,像天线 )传导交流电 的时候,同频率的电磁波也会被发射出来[ 7]
电磁波必然遵守一条定则:不管观察者的速度有多快或多慢,相对于观察者,电磁波永远以光速 传播于真空。爱因斯坦 从这洞察发展出狭义相对论 ,成为狭义相对论的第二条基本原理。
在其它不同于真空的介质内,电磁波传播的速度会小于光速。一个介质的折射率
n
{\displaystyle n\,\!}
c
{\displaystyle c\,\!}
v
{\displaystyle v\,\!}
n
=
c
/
v
{\displaystyle n=c/v\,\!}
按照波长长短,从长波开始,电磁波可以分类为无线电波 、微波 、红外线 、可见光 、紫外线 、X-射线 和伽马射线 等等。普通实验使用的光谱仪 就足以分析从2 奈米 到2500 奈米波长的电磁波。使用这种仪器,可以得知物体、气体或甚至恒星的详细物理性质。这是天文物理学 的必备仪器。例如,因为超精细分裂 ,氢原子 会发射波长为21.12公分的无线电波[ 12]
人类眼睛可以观测到波长大约在400 奈米 和700 奈米 之间的电磁波,称为‘可见光’。
每一种电极性分子 ,会对应着某些特定频率的微波,使得电极性分子随着振荡电场一起旋转 ,这机制称为电介质加热 (dielectric heating )。由于这种机制(不是热传导 机制),电极性分子会吸收微波的能量。微波炉 就是应用这运作原理,通过水分子 的旋转,更均匀地将食物加热,减少等候时间。
麦克斯韦方程组 可以描述电磁波的普遍物理现象。在自由空间 里,源项目等于零(源电荷 等于零,源电流 等于零)。除了没有任何事发生的解以外(电场 和磁场 都等于零),方程仍旧允许不简单的解,电场和磁场随着时间和位置变化[ 7] 国际单位制 ,处于自由空间状况的麦克斯韦方程组表达为
∇
⋅
E
=
0
{\displaystyle \nabla \cdot \mathbf {E} =0\,\!}
(1)
∇
×
E
=
−
∂
B
∂
t
{\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}\,\!}
(2)
∇
⋅
B
=
0
{\displaystyle \nabla \cdot \mathbf {B} =0\,\!}
(3)
∇
×
B
=
μ
0
ϵ
0
∂
E
∂
t
{\displaystyle \nabla \times \mathbf {B} =\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\,\!}
(4) 其中,
E
{\displaystyle \mathbf {E} \,\!}
B
{\displaystyle \mathbf {B} \,\!}
ϵ
0
{\displaystyle \epsilon _{0}\,\!}
真空电容率 ,
μ
0
{\displaystyle \mu _{0}\,\!}
真空磁导率 。
满足上述条件的一个解是
E
=
B
=
0
{\displaystyle \mathbf {E} =\mathbf {B} =\mathbf {0} \,\!}
∇
×
(
∇
×
E
)
=
∇
×
(
−
∂
B
∂
t
)
{\displaystyle \nabla \times \left(\nabla \times \mathbf {E} \right)=\nabla \times \left(-{\frac {\partial \mathbf {B} }{\partial t}}\right)\,\!}
(5) 应用一个矢量恒等式 ,再将公式(1)代入,则可得到:
∇
×
(
∇
×
E
)
=
∇
(
∇
⋅
E
)
−
∇
2
E
=
−
∇
2
E
{\displaystyle \nabla \times \left(\nabla \times \mathbf {E} \right)=\nabla \left(\nabla \cdot \mathbf {E} \right)-\nabla ^{2}\mathbf {E} =-\nabla ^{2}\mathbf {E} \,\!}
(6) 应用公式(4),公式(5)右边变为
∇
×
(
−
∂
B
∂
t
)
=
−
∂
∂
t
(
∇
×
B
)
=
−
μ
0
ϵ
0
∂
2
E
∂
t
2
{\displaystyle \nabla \times \left(-{\frac {\partial \mathbf {B} }{\partial t}}\right)=-{\frac {\partial }{\partial t}}\left(\nabla \times \mathbf {B} \right)=-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}\,\!}
(7) 将公式(6)和(7)代回公式(5),可以得到电场的波动方程 :
∇
2
E
=
μ
0
ϵ
0
∂
2
E
∂
t
2
{\displaystyle \nabla ^{2}\mathbf {E} =\mu _{0}\epsilon _{0}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}\,\!}
使用类似的方法,可以得到磁场的波动方程:
∇
2
B
=
μ
0
ϵ
0
∂
2
B
∂
t
2
{\displaystyle \nabla ^{2}\mathbf {B} =\mu _{0}\epsilon _{0}{\frac {\partial ^{2}\mathbf {B} }{\partial t^{2}}}\,\!}
这两个方程就是真空的电磁波方程 ,描述传播于真空的电磁波。更简易地表达,
◻
E
=
0
{\displaystyle \Box \mathbf {E} =0\,\!}
◻
B
=
0
{\displaystyle \Box \mathbf {B} =0\,\!}
其中,
◻
=
∇
2
−
1
v
0
2
∂
2
∂
t
2
{\displaystyle \Box =\nabla ^{2}-{\frac {1}{{v_{0}}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\,\!}
达朗白算符 ,
v
0
=
1
μ
0
ϵ
0
{\displaystyle v_{0}={\frac {1}{\sqrt {\mu _{0}\epsilon _{0}}}}\,\!}
在自由空间里,
v
0
{\displaystyle v_{0}\,\!}
光速
c
{\displaystyle c\,\!}
ϵ
0
{\displaystyle \epsilon _{0}\,\!}
μ
0
{\displaystyle \mu _{0}\,\!}
c
{\displaystyle c\,\!}
威廉·爱德华·韦伯 与鲁道夫·科尔劳施 发现,但麦克斯韦是首个创造与波在光速传播相一致的场论的人。
前面已经找到了两个方程。但是麦克斯韦方程组有四个方程,所以,还有很多重要的讯息隐藏在这个方程里。思考一个一般的电场矢量波动的解,
E
=
E
0
f
(
k
⋅
r
−
ω
t
)
{\displaystyle \mathbf {E} =\mathbf {E} _{0}f\left(\mathbf {k} \cdot \mathbf {r} -\omega t\right)\,\!}
其中,
E
0
{\displaystyle \mathbf {E} _{0}\,\!}
f
(
.
.
.
)
{\displaystyle f(...)\,\!}
二次可微函数 ,
k
{\displaystyle \mathbf {k} \,\!}
波矢 ,
r
0
{\displaystyle \mathbf {r} _{0}\,\!}
位置矢量 ,
ω
{\displaystyle \omega \,\!}
角频率 。
波动方程
◻
f
=
0
{\displaystyle \Box \mathbf {f} =0\,\!}
f
(
k
⋅
r
−
ω
t
)
{\displaystyle f\left(\mathbf {k} \cdot \mathbf {r} -\omega t\right)\,\!}
∇
2
f
(
k
⋅
r
−
ω
t
)
=
1
c
0
2
∂
2
∂
t
2
f
(
k
⋅
r
−
ω
t
)
{\displaystyle \nabla ^{2}f\left(\mathbf {k} \cdot \mathbf {r} -\omega t\right)={\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}f\left(\mathbf {k} \cdot \mathbf {r} -\omega t\right)\,\!}
将电场的公式代入公式(1):
∇
⋅
E
=
k
⋅
E
0
f
′
(
k
⋅
r
−
ω
t
)
=
0
{\displaystyle \nabla \cdot \mathbf {E} =\mathbf {k} \cdot \mathbf {E} _{0}f'\left(\mathbf {k} \cdot \mathbf {r} -\omega t\right)=0\,\!}
只要电场垂直于波矢(波动传播的方向),这函数形式的电场必定满足麦克斯韦方程组:
E
⋅
k
=
0
{\displaystyle \mathbf {E} \cdot \mathbf {k} =0\,\!}
再将电场的公式代入公式(2):
∇
×
E
=
k
^
×
E
0
f
′
(
k
⋅
r
−
ω
t
)
=
−
∂
B
∂
t
{\displaystyle \nabla \times \mathbf {E} ={\hat {\mathbf {k} }}\times \mathbf {E} _{0}f'\left(\mathbf {k} \cdot \mathbf {r} -\omega t\right)=-{\frac {\partial \mathbf {B} }{\partial t}}\,\!}
所以,电场与其对应磁场的关系为:
B
=
1
ω
k
×
E
{\displaystyle \mathbf {B} ={\frac {1}{\omega }}\mathbf {k} \times \mathbf {E} \,\!}
在自由空间内,电磁波不只是有以光速传播的性质,电磁波的电场部分和磁场部分有特定的相对定向 、相对大小。它们之间的相位 一样。电场,磁场,波动传播的方向,都互相垂直于对方。波动传播的方向是
E
×
B
{\displaystyle \mathbf {E} \times \mathbf {B} \,\!}
从电磁波传播的方向看去,电场或许是以上下的方式震荡,而磁场以左右的方式震荡。但若将这图样旋转90度,则电场以左右的方式震荡,而磁场以上下的方式震荡,而波动传播的方向仍旧相同。这是波动方程的另一种解答。对于波动同样传播的方向,这定向的任意性现象称为偏振 [ 7]
Encyclopædia Britannica Online. James Clerk Maxwell . Encyclopædia Britannica. [2009-08-24 ] . (原始内容存档 于2009-08-31) (英语) . Encyclopædia Britannica Online. Heinrich Hertz . Encyclopædia Britannica. [2009-08-25 ] . (原始内容存档 于2009-09-01) (英语) . Griffiths, David J. Introduction to Electrodynamics (3rd ed.). Prentice Hall. 1998: pp. 364–374, 416–471. ISBN 0-13-805326-X Halliday, David; Robert Resnick, Jearl Walker. Fundamental of Physics 7th. USA: John Wiley and Sons, Inc. 2005. ISBN 0-471-23231-9 Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc., 1999, ISBN 978-0-471-30932-1 Hecht, Eugene, Optics 4th, United States of America: Addison Wesley, 2002, ISBN 0-8053-8566-5(英语)