八维空间

在数学中， 一个n实数的序列可以被理解为n维空间中的一个位置。当n等于八时，所有这样的位置的集合被称为八维空间。 通常这种空间被研究为一个向量空间，而没有任何距离的概念。八维欧几里得空间是一个配备了一个欧几里得距离的八维空间，它由点积定义。

更广义的来说，该术语可以指任何体上的八维向量空间，例如八维复矢量空间，其实际有着十六个维度。 它同时也可能指八维流形例如八维球面，或其它各种几何构造。

几何学中

八维多胞形

主条目：八维多胞形

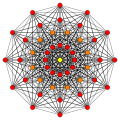
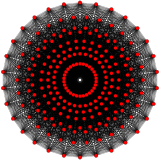
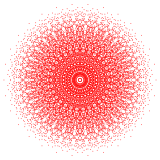
在八维空间中的多胞形都被称为八维多胞形。 最常见的是正多胞形，而这些正多胞形在八维空间中只有三个： 八维单纯形（英语：8-simplex）， 八维超方形（英语：8-cube），八维正轴形（英语：8-orthoplex）。而更广义的类型是八维均匀多胞形，是由反射的基本对称群构造出的，每一个域由考斯特群定义。每一个均匀多胞形是由一个环形考斯特图（英语：Coxeter-Dynkin diagram）定义的。八维半超方形（英语：8-demicube）是一个D8家族中的一个特殊多胞形，而4₂₁（英语：4 21 polytope），2₄₁（英语：2 41 polytope），以及1₄₂（英语：1 42 polytope）则是属于E8家族。

八维空间中的正多胞形以及均匀多胞形
（根据对称性的考斯特平面正交投影）

A8			B8						D8
八维单纯形（英语：8-simplex）			八维超方形（英语：8-cube）			八维正轴形（英语：8-orthoplex）			八维半超方形（英语：8-demicube）
E8（英语：E8 (mathematics)）
421（英语：4 21 polytope）				241（英语：2 41 polytope）				142（英语：1 42 polytope）

七维球面

七维球面，或是八维空间的超球体， 是一个从七维曲面到中心点皆等距的超球体。它的符号为S⁷， 而关于七维球面的方程式，设半径为r，其超球心为

${\displaystyle S^{7}=\left\{x\in \mathbb {R} ^{8}:\|x\|=r\right\}.}$

而这个七维球面在八维空间的体积是

${\displaystyle V_{8}\,={\frac {\pi ^{4}}{24}}\,R^{8}}$

也就是4.05871 × r⁸，而一个八维超立方体中最大的内接八维超球大约等同于该八维超立方体的0.01585倍。

接吻数问题

主条目：接吻数问题

接吻数问题（英语：Kissing_number_problem）可于八维空间中解决，原因在于4₂₁（英语：4 21 polytope）多胞形以及其带关联的点阵群。 在八维空间中的接吻数是240。

八元数

主条目：八元数

八元数是是实数的可除代数，八元数是有最高维度的可除代数（十六元数或更高的元数不是可除代数，因为他们存在零因子）。在数学中，它们可以由实数八元数来区别，所以形成一个真实的八维向量空间，有着一个附加的向量，是代数中的附加。 一个规范代数是一个有者着积的代数并对于所有代数中的x和y符合以下公式：

${\displaystyle \|xy\|\leq \|x\|\|y\|}$

其中一个范例多元体另外必须是有限维的，并有着每一个非零的向量有一个特殊倒数的属性胡尔维兹定理禁止像四元数以及八元数这样的代数结构在除了1，2，4和8之外的维度的存在。

由于八元数的乘法没有结合律，所以与四元数不同，他们没有矩阵的表示法，因为矩阵的乘法一定有结合律，也同样因此，非零八元数的乘法运算不构成群。

复四元数

复杂的四元数 ${\displaystyle \mathbb {C} \otimes \mathbb {H} }$，或称为“复四元数”，是一个威廉·哈密顿于1850年对于八维代数的研究。这个代数同等于（“同等”一词在此指同构）克里福代数${\displaystyle C\ell _{2}(\mathbb {C} )}$ 以及泡利矩阵。 它也被提议做为在狭义相对论中进行运算的用具，而此运算用具的名称为“物理空间代数（英语：Algebra of physical space）”。（不要与有十六个维度的时空代数混淆了。）

参见

• 次元

参考资料

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter（页面存档备份，存于互联网档案馆）
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Table of the Highest Kissing Numbers Presently Known（页面存档备份，存于互联网档案馆） maintained by Gabriele Nebe and Neil Sloane (lower bounds)
• Conway, John Horton; Smith, Derek A., On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, A. K. Peters, Ltd., 2003, ISBN 1-56881-134-9. (Review（页面存档备份，存于互联网档案馆）).
• Duplij（乌克兰语：Дуплій Степан Анатолійович）, Steven; Siegel, Warren; Bagger, Jonathan (编), Concise Encyclopedia of Supersymmetry And Noncommutative Structures in Mathematics and Physics, Berlin, New York: Springer, 2005, ISBN 978-1-4020-1338-6 (Second printing)