热门问题
时间线
聊天
视角
辫群
数学概念 来自维基百科,自由的百科全书
Remove ads
辫群(英语:Braid group)为数学领域中纽结理论的一个概念。一个 股的辫群(记为)是元素为 n-braid 的群,其运算为前一个 n-braid 按后一个 n-braid 的方式操作(见 § 举例说明)。

辫群是由美国数学家埃米尔·阿廷(于1925 年提出[1]),因此又被称为阿廷辫群(英语:Artin Braid group)。[2]
Remove ads
引言
想像有4条横著摆放的绳子,它们的两端分别被固定在左右两侧的墙上。如下图所示,黑点代表被固定的位置。

我们称这样绳子的摆放方式,或是编织的方式为一个辫子(英语:braid)。而正式的写法中会连绳子的数目也一起表达,将4股的辫子以英文简写成 4-braid。
如果将刚才的辫子中下面两条的右端交换位置,会变成下图的样子。

那么这两种会是不同的4股辫子(英语:4-braid)。 如果将这两种辫子理解为群中的元素,那么刚才把右端交换位置的操作就是群当中的运算。在辫群的讨论中,常用这些操作来表示不同的辫子,这种表示方法称作 braid word。[2]
举例说明
在这个小节中,以为例。
下面的两条辫子是不同的:

|
不同于 | 
|
但是下面的两条辫子是相同的:

|
同于 | 
|
所有的股都必须从左向右移动,所以下面的图片并不是一条辫子:

|
不是辫子 |
我们可以编两条辫子:

|
加 | 
|
等于 | 
|
另一个例子:

|
加 | 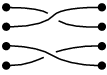
|
等于 | 
|
复合 / 编织物σ和τ的组成写为στ。
Remove ads
应用
辫群的应用包括 陈-西蒙斯理论、亚历山大定理(Alexander's Theorem)、杨-巴克斯特方程、 代数几何、任意子、等。[3]
参见
参考文献
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads




