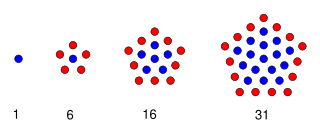
有形数是可以排成有一定规律形状的数。有形数是毕达哥拉斯学派的关注重点之一,他们认为数和形有不可分割的关系。有形数都是自然数,它们可以用小石子堆砌。有形数是将数形象化的方法。
此条目没有列出任何参考或来源。 (2019年1月9日) |
一般地,任意一个自然数都可以表示为n个n边形数的和。(此即费马多边形数定理)
前几个平面上的有形数为:(不考虑trivial case,也就是n为n边形数的情形)
6, 9, 10, 12, 15, 16, 18, 21, 22, 24, 25, 27, 28, 30, 33, 34, 35, 36, 39, 40, 42, 45, 46, 48, 49, 51, 52, 54, 55, 57, 58, 60, 63, 64, 65, 66, 69, 70, 72, 75, 76, 78, 81, 82, 84, 85, 87, 88, 90, 91, 92, 93, 94, 95, 96, 99, 100, ... (OEIS数列A090466)
种类
有形数可依照该数能排成的形状分成:
例子
能排成三角形的有形数
前17个三角形数是
能排成等腰梯形的有形数
| 2 | 7 | 15 | ||
|---|---|---|---|---|
前15个梯形数为
梯形数公式:(顶层数+底层数)×层数÷2
排成从中心延伸出去的五边形
前15项的中心五边形数为
能堆成四角锥的有形数
能排成六角星的有形数
| 1 | 13 | 37 | ||
|---|---|---|---|---|
前13个六角星数是
参见
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.