吸引子

吸引子（Attractor）是微积分和系统科学论中的一个概念。一个系统有朝某个稳态发展的趋势，这个稳态就叫做吸引子。

吸引子分为平庸吸引子和奇异吸引子（Strange Attractor）。例如一个钟摆系统，它有一个平庸吸引子，这个吸引子使钟摆系统向停止晃动的稳态发展。平庸吸引子有不动点（平衡）、极限环（周期运动）和整数维环面（概周期运动）三种模式。而不属于平庸的吸引子的都称为奇异吸引子，它表现了混沌系统中非周期性，无序的系统状态，例如天气系统。

对于吸引子，学术上并没有完善的定义，目前仅处于概念阶段。吸引子中的奇异吸引子对于混沌系统的研究意义重大。

定义

设${\displaystyle t}$代表时间、${\displaystyle f(t,\cdot )}$是用来确定动力系统状态的函数。也就是说，如果${\displaystyle a}$是${\displaystyle n}$维相空间的一个点，代表系统的初始状态，则${\displaystyle f(0,a)=a}$且对每个正实数${\displaystyle t}$有${\displaystyle f(t,a)}$代表经过${\displaystyle t}$单位时间后的状态。举例来说，如果一系统描述一维上某不受力粒子的演进，此时相空间是平面${\displaystyle \mathbb {R} ^{2}}$，其坐标${\displaystyle (x,v)}$中的${\displaystyle x}$是粒子的位置，${\displaystyle v}$是粒子的速度。那么就有

${\displaystyle f(t,(x,v))=(x+tv,v).\ }$

而吸子是相空间中的子集${\displaystyle A}$，并有以下几个特征：

• ${\displaystyle A}$在${\displaystyle f}$下不随时间变化，从而如果${\displaystyle a\in A}$就有${\displaystyle f(t,a)\in A}$对所有正实数${\displaystyle t}$。
• 存在${\displaystyle A}$的邻域${\displaystyle B(A)}$（英文是basin of attraction），使得该域中任何点在时间趋于无限时都会趋近${\displaystyle A}$，或者更精准的是满足以下叙述：

对任何${\displaystyle A}$的邻域${\displaystyle N}$和${\displaystyle b\in B(A)}$，存在正实数${\displaystyle T}$使得${\displaystyle f(t,b)\in N}$对所有${\displaystyle t>T}$。

• 不存在${\displaystyle A}$的非空子集可以取代${\displaystyle A}$满足前面两点性质。

吸子还有许多其它种的定义，例如有些作者要求吸子有正的测度（以避免吸子中只有一个点），但其他作者只要求${\displaystyle B(A)}$是邻域^[1]。

种类

吸子是动力系统中相空间的子集。在公元1960年代前，吸子仍被认为有“简单的”几何形状，例如点、直线、平面等。但吸子的形状事实上可能相当复杂， 斯梅尔证明其马蹄映射的吸子有康托尔集的结构。

两种简单的吸子是不动点和极限环。也有的吸子无法使用基本的几何对象的组合来描述，那么他就被称作奇异吸子。

不动点

有限个点

极限环

主条目：极限环

极限环面

奇异吸子

洛伦茨奇异吸子的图，其中用到参数ρ=28, σ = 10, β = 8/3。

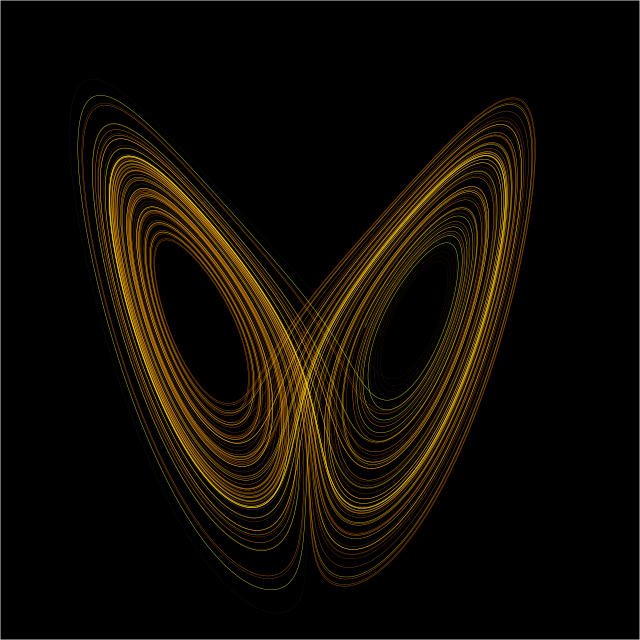
一个吸子被称为奇异（strange）如果他具有分形结构^[2]，这常常出现在动力系统是混乱的时，但奇异非混乱吸子也是存在的。

若一奇异吸子是混沌的，则其对初始条件敏感。也就是任意两个极为接近的初始点，在一定数量的迭代运算后，两者可以相距甚远；也可以再经过一定数量的迭代运算后又变得极为靠近。也因此，一个具有混沌吸子的动力系统在局域是不稳定的，然而广域来看却可以是稳定的，因为这些动态点再怎么彼此分离，也都不会离开吸子。

奇异吸子这个词最早是由吕埃勒与Floris Takens（英语：Floris Takens）所命名，用以描述流体系统经一连串分岔所产生的吸子结果。^[3]

奇异吸子在一些方向上常是可微的，但一些例子则如同康托尘则不可微。奇异吸子亦可出现在有噪声的场合。^[4]

奇异吸子的例子包括多卷波混沌吸引子、艾侬吸子、热斯勒吸子，以及洛伦茨吸子。

参考资料

1. Milnor, J. (1985). "On the Concept of Attractor." Comm. Math. Phys 99: 177–195.
2. Boeing, G. Visual Analysis of Nonlinear Dynamical Systems: Chaos, Fractals, Self-Similarity and the Limits of Prediction. Systems. 2016, 4 (4): 37 [2016-12-02]. arXiv:1608.04416 . doi:10.3390/systems4040037. （原始内容存档于2016-12-03）.
3. Ruelle, David; Takens, Floris. On the nature of turbulence. Communications in Mathematical Physics. 1971, 20 (3): 167–192 [2019-07-22]. doi:10.1007/bf01646553. （原始内容存档于2015-06-23）.
4. Chekroun M. D., Simonnet E., and Ghil M. Stochastic climate dynamics: Random attractors and time-dependent invariant measures. Physica D. 2011, 240 (21): 1685–1700. doi:10.1016/j.physd.2011.06.005.