Hyperoctahedral group

conjecture）即是说这个由2d 个点组成的集合是在这距离下最大的等距集。 正图形 超正八面体对称群（英语：Hyperoctahedral group），正轴形的对称群。 Elte（英语：Emanuel Lodewijk Elte）, E. L., 超空间中的半正多胞形, 格罗宁根:

digram）为，对应考克斯特BC4平面（即超方形—正轴形对应的考克斯特平面（英语：Coxeter Plane）），具有超正八面体对称性（英语：Hyperoctahedral group#By dimension）（又叫正十六胞体对称性），阶为384。同时，它也可被看作是立方体的四维棱柱，对应施莱夫利符号{4

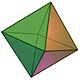
其的不同面拥有不同的“几何意义”，使正八面体拥有不同的对称性。正八面体的对称群是Oh（正八面体群），是三维的超正八面体群（英语：Hyperoctahedral group）。在此对称性下，正八面体的所有面都带有相同对“颜色”，对称性最高，群阶48。该群的子群体现了正八面体更低的对称性：Td（群阶2

这个特殊关系可以被用来高效地产生(n-1)-单纯形的表面框架，毕竟可用于计算所有多胞形表面框架的一般方法在计算上比较困难。 超正八面体对称群（英语：Hyperoctahedral group），超方形的对称性 超球面 单纯形 超立方体互联网络，网络工程学 Elte, E. L. The Semiregular Polytopes

四維凸正多胞體 對稱群 A4 B4（英语：Hyperoctahedral_group） F4（英语：F4 (mathematics)） H4（英语：H4 polytope） 名稱 正五胞體 超四面體 正十六胞體 超八面體 四維超正方體 超立方體 正二十四胞體 正六百胞體 超二十面體 正一百二十胞體