散点图（scatter plot、scatterplot、scatter graph、scatter chart、scattergram或scatter diagram）[3]是用笛卡尔坐标系上的点表示资料中二个或多个变数分布方式的图（例如班上同学的身高及体重）。多半是在平面笛卡尔坐标上，表示二个变数的分布，若点有区分不同的颜色／形状／大小，可以用此特性表示另一个变数。
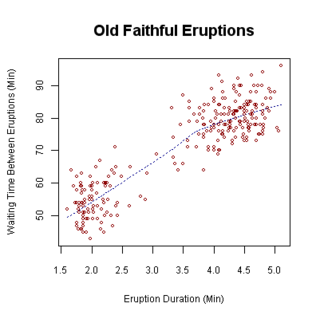
散点图中的资料会用许多的点来表示，每个点表示一个资料，而其在水平坐标轴及垂直坐标轴上的坐标，分别对应该资料的变数[4]。
简介
散点图可以用来表示实验中的连续自变量和另一个连续因变量之间的关系，也可以用来表示二个连续自变量之间的关系。若系统中存在参数，在实验中会刻意增加或减少其数值，此参数即为自变量，若是自变量和因变量的散点图，一般会将自变量放在横轴，因变量放在纵轴。若两个参数都是自变量，可将任一个放在横轴，此时，散点图可以看出其相关性的程度（但不一定是因果关系）。
散点图可以推测二个参数中许多不同种类的相关性，配合一定的置信区间。以体重及身高为例，可能会将体重放在y轴，将身高放在x轴。相关性可能是正相关（一参数增加时，另一参数对应增加）、负相关（一参数增加时，另一参数对应减少）、无相关性。若散点图有从左下到右上分布的图形，表示两者正相关，若散点图有从左上到右下分布的图形，表示两者负相关。为了研究两参数之间的关系，可以在散点图上绘制拟合线（最适曲线、或趋势线）。趋势线的方程式就是参数相关性的方程式。若是线性相关，绘制最适曲线的程序即为线性回归，保证在有限时间内有正确的解。针对任意的相关性关系，不存在通用、可以产生正确解的最适曲线产生程序。若是要确认两组参数之间是否有非线性的关系，也可以用散点图来观察。可以在散点图中加上平滑曲线（例如LOESS）来达到此一机能[5]。若数据可以表示为简单关系的混合模型表示，其关系在视觉上上会是以叠加模式来表示。
例子
例如，为了要找到人肺容量以及其闭气时间之间的关连性，研究者找了一群人进行研究，量测肺容量（第一个变量）及可以闭气的时间（第二个变量），接着就可以画散点图，以肺容量为横轴，闭气的时间为纵轴。
若有一个人其肺容量是400 cl，可以闭气21.7秒，则此数据会表示为坐标(400, 21.7)的点，将所有人的资料都画在一张图上，可以让研究者判断两个变量之间的关系。
散点图矩阵
针对一组（超过二个）的资料变量X1, X2, ... , Xk，可以用散点图矩阵（scatter plot matrix）画出两两变量之间的散点图，而多个散点图以矩阵的形式放在同一个大图中。散点图矩阵会有k栏k列的方阵。其中每一个元素都是对应二个变量之间的散点图[8]。每一栏和每一列都是一个维度，而矩阵中的每一个元素都是二维下的散点图。
通用散点图矩阵（generalized scatter plot matrix）[9]提供各种变量（量化变量以及分类变量）之间的成对关系。马赛克图、波动图或多面条形图可以表示两个分类变量之间的关系。也有其他的图可以说明量化变量以及分类变量之间的关系。
相关条目
参考资料
外部链接
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
