孤點

在拓撲學中，考慮集合X中的點x，如果x屬於X的子集S，且在X中存在一個x的鄰域，其中不包括S中的其他點，那麼x叫做子集S的一個孤點或孤立點。

"0" is an isolated point of A

特別的，在歐幾里得空間（或度量空間）中，考慮集合S及其中的一個點x，如果存在一個包含x的開球，其中不包含S中的其他點，那麼x是S的孤點。等價的說，集合S中的一個點x是孤點，若且唯若x不是S的會聚點。

只由孤點構成的集合稱為離散集合。歐幾里得空間的離散子集都是可數的；但是一個可數集合不一定是離散的，比如有理數。參見離散空間。

沒有孤點的集合叫做完美集合。

孤點的數目是拓撲不變的，就是說兩個同胚的拓撲空間${\displaystyle X}$和${\displaystyle Y}$有相同數目的孤點。

舉例

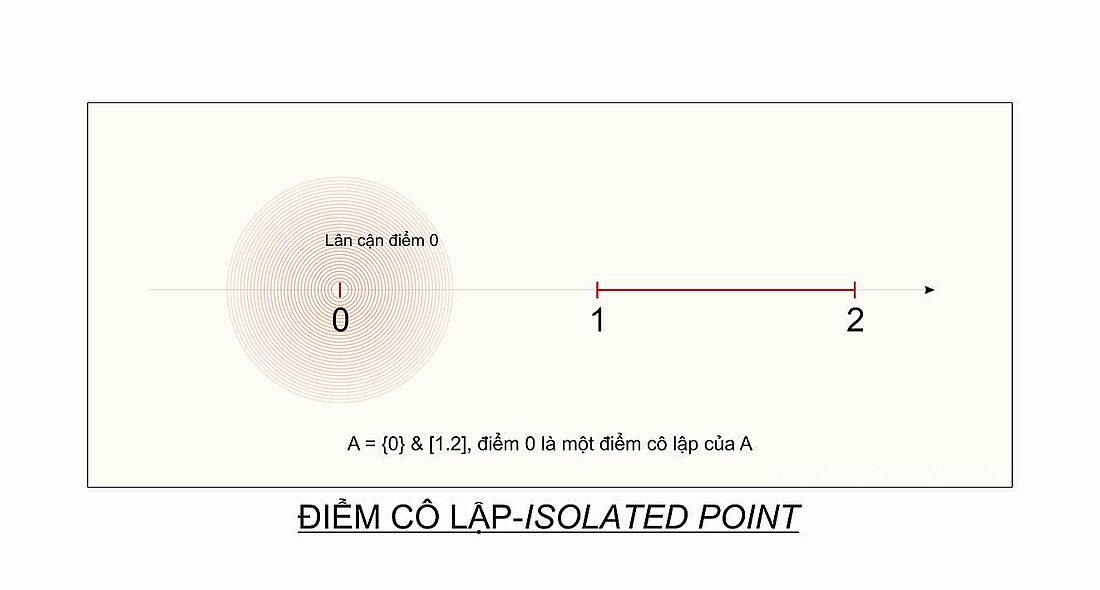
• 對集合${\displaystyle S=\{0\}\cup [1,2]}$，點0是孤點。
• 對集合${\displaystyle S=\{0\}\cup \{1,1/2,1/3,\dots \}}$，每一個點1/k是孤點，但0不是孤點，因為在S中可以找到任意接近0的點。
• 自然數集合N={0, 1, 2, ...}是一個離散集合。

外部連結

• https://web.archive.org/web/20080415075029/http://www.cool-rr.com/protein.htm Rigorous proof of isolated points' countability.