雙球坐標系

雙球坐標系（英語：Bispherical coordinates）是一種三維正交坐標系。設定二維雙極坐標系包含於 xz-平面。設定這雙極坐標系的兩個焦點 ${\displaystyle F_{1}}$ 與 ${\displaystyle F_{2}}$ 包含於 z-軸。將雙極坐標系繞着 z-軸旋轉，則可以得到雙球坐標系。在這二維雙極坐標系裏，坐標 ${\displaystyle \sigma }$ 的等值曲線是圓圈。 經過旋轉後，圓圈變成一個環面，而圓圈的圓心變成一個包含於 xy-平面的圓圈，稱為環心圓。稱環心圓至環面的距離為環小半徑。

圖 1 ）雙球坐標系的幾個坐標曲面。紅色環面的 ${\displaystyle \sigma =45^{\circ }}$ 。藍色圓球面的 ${\displaystyle \tau =0.5}$ 。黃色半平面的 ${\displaystyle \phi =60^{\circ }}$ 。z-軸是垂直的，以白色表示。 x-軸以綠色表示。三個坐標曲面相交於點 P （以黑色的圓球表示），直角坐標大約為 ${\displaystyle (0.841,\ -1.456,\ 1.239)}$ 。

圖 2 ）雙極坐標系繪圖。紅色圓圈變成上圖的紅色環面（ ${\displaystyle \sigma }$-坐標曲面），而藍色圓圈則變成藍色圓球面（ ${\displaystyle \tau }$-坐標曲面）。

基本定義

在三維空間裏，一個點 P 的雙球坐標 ${\displaystyle (\sigma ,\ \tau ,\ \phi )}$ 最常見的定義是

${\displaystyle x=a\ {\frac {\sin \sigma }{\cosh \tau -\cos \sigma }}\cos \phi }$ 、

${\displaystyle y=a\ {\frac {\sin \sigma }{\cosh \tau -\cos \sigma }}\sin \phi }$ 、

${\displaystyle z=a\ {\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}}$ ；

其中，${\displaystyle (x,\ y,\ z)}$ 是直角坐標，${\displaystyle \sigma }$ 坐標是 ${\displaystyle \angle F_{1}PF_{2}}$ 的弧度，${\displaystyle \tau }$ 坐標是點 P 離兩個焦點的距離 ${\displaystyle d_{1}}$ 與 ${\displaystyle d_{2}}$ 的比例的自然對數：

${\displaystyle \tau =\ln {\frac {d_{1}}{d_{2}}}}$ 。

坐標曲面

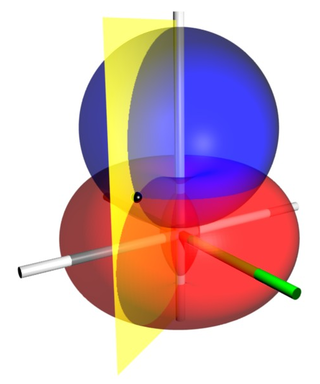
每一個紅色的 ${\displaystyle \sigma }$-坐標曲面都是包含了兩個焦點 ${\displaystyle F_{1}}$ 與 ${\displaystyle F_{2}}$ 環面。，每一個環面的環心圓都不相同。這些環心圓都包含於 xy-平面。環小半徑為

${\displaystyle z^{2}+\left({\sqrt {x^{2}+y^{2}}}-a\cot \sigma \right)^{2}={\frac {a^{2}}{\sin ^{2}\sigma }}}$ 。

當絕對值 ${\displaystyle \left|\sigma \right|}$ 增加時，環小半徑會減小，環心圓會靠近原點。當環心圓與原點同點時，${\displaystyle \left|\sigma \right|}$ 達到最大值 ${\displaystyle \pi /2}$ 。

每一個藍色的 ${\displaystyle \tau }$-坐標曲面都是不相交的圓球面。每一個圓球面都包圍着一個焦點；圓球心都包含於 z-軸。圓球半徑為

${\displaystyle x^{2}+y^{2}+(z-a\coth \tau )^{2}={\frac {a^{2}}{\sinh ^{2}\tau }}}$ 。

它們的圓球心都包含於 z-軸。正值 ${\displaystyle \tau }$ 的圓球面在 ${\displaystyle z>0}$ 半空間；而負值 ${\displaystyle \tau }$ 的圓球面在 ${\displaystyle z<0}$ 半空間。${\displaystyle \tau =0}$ 曲線則與 xy-平面同平面。當 ${\displaystyle \tau }$ 值增加時，圓球面的半徑會減少，圓球心會靠近焦點。

逆變換

圖 3 ）點 P 的坐標 ${\displaystyle \sigma }$ 與 ${\displaystyle \tau }$ 的幾何意義。在一個方位角 ${\displaystyle \phi }$ 為常數的平面裏，雙球坐標系變成雙極坐標系。${\displaystyle \sigma }$ 是角 ${\displaystyle \angle F_{1}PF_{2}}$ 的弧度。${\displaystyle \tau }$ 是點 P 離兩個焦點的距離 ${\displaystyle d_{1}}$ 與 ${\displaystyle d_{2}}$ 的比例的自然對數。${\displaystyle \sigma }$ 與 ${\displaystyle \tau }$ 的等值曲線都是圓圈，分別以紅色與藍色表示。兩條等值曲線以直角相交（表示在洋紅色的方盒裏）。

雙球坐標 ${\displaystyle (\sigma ,\ \tau ,\ \phi )}$ 可以用直角坐標 ${\displaystyle (x,\ y,\ z)}$ 來表示。方位角 ${\displaystyle \phi }$ 的公式為

${\displaystyle \tan \phi ={\frac {y}{x}}}$ 。

點 P 與兩個焦點之間的距離是

${\displaystyle d_{1}^{2}=x^{2}+y^{2}+(z+a)^{2}}$ 、

${\displaystyle d_{2}^{2}=x^{2}+y^{2}+(z-a)^{2}}$ 。

${\displaystyle \tau }$ 是 ${\displaystyle d_{1}}$ 與 ${\displaystyle d_{2}}$ 的比例的自然對數：

${\displaystyle \tau =\ln {\frac {d_{1}}{d_{2}}}}$ 。

如圖 3 ，${\displaystyle \angle F_{1}PF_{2}}$ 是兩條從點 P 到兩個焦點的線段 之間的夾角。這夾角的弧度是 ${\displaystyle \sigma }$ 。用餘弦定理來計算：

${\displaystyle \cos \sigma ={\frac {d_{1}^{2}+d_{2}^{2}-4a^{2}}{2d_{1}d_{2}}}}$ 。

標度因子

雙球坐標 ${\displaystyle \sigma }$ 與 ${\displaystyle \tau }$ 的標度因子相等：

${\displaystyle h_{\sigma }=h_{\tau }={\frac {a}{\cosh \tau -\cos \sigma }}}$ 。

方位角的標度因子為

${\displaystyle h_{\phi }={\frac {a\sin \sigma }{\cosh \tau -\cos \sigma }}}$ 。

無窮小體積元素是

${\displaystyle dV={\frac {a^{3}\sin \sigma }{(\cosh \tau -\cos \sigma )^{3}}}d\sigma d\tau d\phi }$ 。

拉普拉斯算子是

${\displaystyle \nabla ^{2}\Phi ={\frac {\left(\cosh \tau -\cos \sigma \right)^{3}}{a^{2}\sin \sigma }}\left[{\frac {\partial }{\partial \sigma }}\left({\frac {\sin \sigma }{\cosh \tau -\cos \sigma }}{\frac {\partial \Phi }{\partial \sigma }}\right)+\sin \sigma {\frac {\partial }{\partial \tau }}\left({\frac {1}{\cosh \tau -\cos \sigma }}{\frac {\partial \Phi }{\partial \tau }}\right)+{\frac {1}{\sin \sigma \left(\cosh \tau -\cos \sigma \right)}}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}\right]}$ 。

其它微分算子，像 ${\displaystyle \nabla \cdot \mathbf {F} }$ ， ${\displaystyle \nabla \times \mathbf {F} }$ ，都可以用 ${\displaystyle (\sigma ,\ \tau ,\ z)}$ 坐標表示，只要將標度因子代入在正交坐標系條目內對應的一般公式。

應用

雙球坐標有一個經典的應用，這是在解析像拉普拉斯方程或亥姆霍茲方程這類的偏微分方程式。在這些方程式裏，雙球坐標允許分離變數法的使用。一個典型的例題是，有兩個不同半徑的圓球導體，請問其周圍的電位與電場為什麼？應用雙球坐標，我們可以精緻地分析這個問題。

參閱

參考目錄

• Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 665–666. 引文格式1維護：冗餘文本 (link)
• Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 182. 引文格式1維護：冗餘文本 (link)
• Zwillinger D. Handbook of Integration. Boston, MA: Jones and Bartlett. 1992: p. 113. ISBN 0-86720-293-9. 引文格式1維護：冗餘文本 (link)
• Moon PH, Spencer DE. Toroidal Coordinates (η, θ, ψ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions 2nd ed., 3rd revised printing. New York: Springer Verlag. 1988: pp. 110–112 (Section IV, E4Ry). ISBN 0-387-02732-7. 引文格式1維護：冗餘文本 (link)