剪切模量
来自维基百科,自由的百科全书
剪力模數(shear modulus)是材料力學中的名詞,彈性材料承受剪應力時會產生剪應變,定義為剪應力與剪應變的比值。公式記為
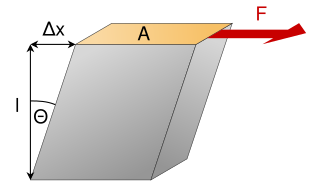
其中, 表示剪力模數, 表示剪應力, 表示剪應變。在均質且等向性的材料中:
波
在均勻各向同性固體中,有兩種波:P波和S波。剪切波的速度,由剪切模量控制,
其中
- G是剪切模量
- 是固體的密度.
金屬的剪切模量

金屬的剪切模量通常隨溫度的升高而降低。在高壓下,剪切模量也隨外加壓力的增大而增大。在許多金屬中,熔點溫度、空位形成能和剪切模量之間的關係已經被觀察到。[3]
有幾種模型試圖預測金屬的剪切模量(可能還有合金的剪切模量)。在塑性流動計算中使用的剪切模量模型包括:
MTS剪切模量模型為:
其中為處的剪切模量,和為材料常數。
剪切鬆弛模量
參見
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
















